Un ejercicio de calentamiento escolar para ocupar su tiempo - página 7

Nuevo comentario
 
Nikolai Semko:
¿Lo es?
En este momento no está en el ordenador.
Creo que lo he probado. ME no reconoció esta función y no la encontró en la ayuda por F1
Tengo entendido que es una biblioteca AlgLib

https://www.mql5.com/ru/docs/standardlibrary/mathematics/stat/mathsubfunctions/statmathsum

 
Aleksey Nikolayev:

https://www.mql5.com/ru/docs/standardlibrary/mathematics/stat/mathsubfunctions/statmathsum

Sí. Aplicación ...

Es un lib, se supone que es así:

1. A cero el array devuelve el valor inicializado por el constructor por defecto (para los primitivos es 0)

template<typename T>
T MathSum(const T &arr[]){
   T sum=T();
   for (int i=0,size=ArraySize(arr);i<size;sum+=arr[i++]);
   return sum;
}

2. En la matriz cero, se bloquea en tiempo de ejecución.

template<typename T>
T MathSum(const T &arr[]){
   T sum=arr[0];
   for (int i=1,size=ArraySize(arr);i<size;sum+=arr[i++]);
   return sum;
}

3. Devuelve una estructura que contiene el código de resultado y el importe

template<typename T>
struct SRet{
   int retCode; //0 - Ок, -1 - Not initialized
   T res;
   SRet():retCode(-1){}
   SRet(uint code,const T &_res):retCode(code),res(_res){}
   SRet(const SRet<T> &other) {this=other;}
   bool operator !() const {return retCode!=0;}
};

template<typename T>
SRet<T> MathSum(const T &arr[]){
   int size=ArraySize(arr);
   if (!size) return SRet<T>();
   SRet<T> ret(0,arr[0]);
   for (int i=1,size=ArraySize(arr);i<size;ret.res+=arr[i++]);
   return ret;
}

El método se llama "lo que quieras"))

Lo escribí a mano, así que tal vez metí la pata en alguna parte.

 
Aleksey Nikolayev:
El teorema de Cramer está en este libro (Apéndice, página 102).

gracias! resulta muy fácil de demostrar a través del (complicado) teorema del círculo.

 
Vladimir Simakov:

Sí. Aplicación ...

Es un lib, se supone que es así:

1. A cero el array devuelve el valor inicializado por el constructor por defecto (para los primitivos es 0)

2. En la matriz cero, se bloquea en tiempo de ejecución.

3. Devuelve una estructura que contiene el código de resultado y el importe

El método se llama "lo que quieras"))

Lo escribí a mano, así que tal vez metí la pata en alguna parte.

Bueno, se escribió: "lo hacemos como en R pero más rápido", ya que en C++ no se prometió.

 
Aleksey Nikolayev:

Bueno, se escribió "hacer como en R, sólo que más rápido", ya que en C++ no se promete.

Excusa débil.

Haciendo como en R... No lo sé, R no está en mi pila.

Excepto, no usar plantillas cuando se escribe una biblioteca en C++ (si parece C++, huele a C++ e incluso tiene UB, eso es sugerente...) - es de alguna manera ...

 
Aleksey Nikolayev:

https://www.mql5.com/ru/docs/standardlibrary/mathematics/stat/mathsubfunctions/statmathsum

Está en la ayuda, pero el compilador no lo ve.
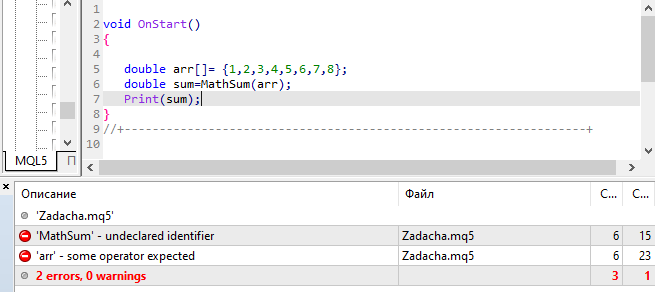
¿Soy yo?


Acabo de ver que tienes

#include <Math\Stat\Math.mqh>

Así que debe ser una biblioteca externa.
Una vez más, no veo el sentido de cargar tu programa con bibliotecas adicionales sólo para ahorrar una sola línea de código.

 
Nikolai Semko:


Una vez más, no veo el sentido de cargar el programa con bibliotecas adicionales para ahorrar una sola línea de código.

El programa para el caso especial es - es. Las objeciones sobre MathSum son insignificantes

en el fondo de un problema más esencial: arriba se ha notado que esta solución funciona sólo si el centro del círculo circunscrito entra dentro de la figura.

Es decir, necesitamos otro criterio de aplicabilidad. "para este eres bienvenido, pero para este no puedo".

Ahora el tema está directamente relacionado con la optimización del optimizador...

 
Maxim Kuznetsov:

el programa para el caso especial está ahí - está ahí. Las objeciones sobre MathSum son insignificantes

sobre el fondo de un problema más esencial: arriba se ha observado que esta solución sólo funciona si el centro del círculo circunscrito cae dentro de la figura.

Es decir, necesitamos otro criterio de aplicabilidad. "para este eres bienvenido a obtener resultados, pero para este no puedo".

Ahora el tema está directamente relacionado con la optimización del optimizador...

A primera vista, sólo cambiará la ecuación para determinar R.

1) En el caso del centro interior: A1+A2+...+An=2*Pi
2) En el caso del centro exterior: A1-A2-...-An=0, donde A1 es el ángulo del lado más largo.

Por lo tanto, sólo tenemos que determinar cómo distinguir entre los dos casos.

PS. En general, hay que calcular la suma de los ángulos Ai siempre que el radio sea igual a la mitad del lado máximo. Si es menor que 2*Pi, entonces el centro está fuera del polígono y viceversa.

 
Maxim Kuznetsov:

el programa para el caso especial está ahí - está ahí. Las objeciones sobre MathSum son insignificantes

sobre el fondo de un problema más esencial: arriba se ha observado que esta solución sólo funciona si el centro del círculo circunscrito cae dentro de la figura.

Es decir, necesitamos otro criterio de aplicabilidad. "para este eres bienvenido, pero para este no puedo".

Ahora el tema es directamente relevante para la optimización del optimizador...

¿Por qué no puedo hacerlo?
Sólo necesita tiempo para pasar, pero para qué propósito - no está claro.

Creo que Simakov ya lo hizo. Es cierto, no lo entendí.

Muy bien, lo intentaré a mi manera. Para que todo sea visualmente claro.

 

Archivos adjuntos:
Zadacha3.mq5  9 kb
12345678
Nuevo comentario