Existen las siguientes referencias sobre el tema "Fundamentos del análisis de regresión".
Davidson,Russell y James G. MacKinnon (1993). Estimation and Inference inEconometrics, Oxford: Oxford University Press.
Greene, William H. (2008). Econometric Analysis, 6ª edición, Upper Saddle River, NJ: Prentice-Hall.
Johnston, Jack y John Enrico DiNardo (1997). Econometric Methods, 4ª edición, Nueva York: McGraw-Hill.
Pindyck, Robert S. y Daniel L. Rubinfeld (1998). Econometric Models and Economic Forecasts, 4ª edición, Nueva York: McGraw-Hill.
Wooldridge, Jeffrey M. (2000). Introductory Econometrics: A Modern Approach. Cincinnati, OH: South-Western College Publishing.
Te voy a poner un ejemplo de regresión, que no es más que una función (variable dependiente) que depende de sus argumentos (variables independientes, regresores). Hay que seguir varios pasos para calcular una regresión:
1. Hay que escribir una ecuación.
Tomo el MA tan favorecido, pero ponderado, tan indulgente para mí, calculándolo con las 5 barras anteriores (valores de retardo). Escribo la fórmula en la forma
EURUSD = C(1)*EURUSD(-1) + C(2)*EURUSD(-2) + C(3)*EURUSD(-3) + C(4)*EURUSD(-4) + C(5)*EURUSD(-5)
2. estimación
Es necesario estimar el coeficiente c(i) de esta ecuación para que la curva de nuestra MA se corresponda lo mejor posible con la serie inicial de EURUSD_H1 años. Obtenemos el resultado de la evaluación de los coeficientes desconocidos.
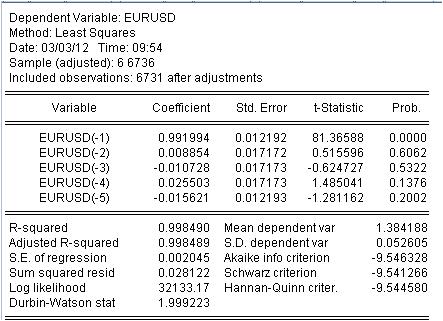
Hemos obtenido los valores de nuestro MA ponderado. Tenemos la ecuación:
EURUSD = 0,991993934254*EURUSD(-1) + 0,00885362355538*EURUSD(-2) - 0,0107282369642*EURUSD(-3) + 0,0255027160774*EURUSD(-4) - 0,0156205779585*EURUSD(-5)
3. Resultados.
¿Qué resultados vemos?
3.1 En primer lugar, la propia ecuación de Mach. Quiero prestar atención a un pequeño matiz. Cuando calculamos una máscara simple calculando la media, no la registramos en la mitad del intervalo sino en su final por alguna razón. La regresión se utiliza para calcular el último valor a partir de los anteriores.
3.2 Resulta que los coeficientes no son constantes, sino variables aleatorias con su propia desviación.
3.3. La última columna dice que hay una probabilidad no nula de que los coeficientes dados sean cero en absoluto.
4. Trabajar con la ecuación
Echemos un vistazo a nuestra mezcla ponderada.

La mashka ha cubierto tanto el cotier que no se ve, pero sigue habiendo discrepancias entre el cotier y la mashka. Estas son las estadísticas de estas discrepancias

Vemos una enorme dispersión de -137 puntos a 215 puntos. Aunque la desviación estándar = 20 puntos.
Conclusión.
Hemos recibido una calidad inusual de la máscara con las características estadísticas conocidas mediante regresión.
El último. ¡Yusuf! No te metas debajo del tranvía, no hagas reír al público en un hilo más.
Listo para discutir la literatura y la aplicación del tema de la regresión.
3. Resultados.
¿Qué resultados vemos?
3.1 En primer lugar, la propia ecuación de Mach. Quiero señalar una sutileza aquí. Cuando calculamos una máscara simple obteniendo la media, por alguna razón no colocamos esta media en el centro del intervalo, sino en su extremo. La regresión se utiliza para calcular el último valor a partir de los anteriores.
3.2 Resulta que los coeficientes no son constantes, sino variables aleatorias.
3.3 La última columna dice que hay una probabilidad no nula de que los coeficientes dados sean cero.
1. perdón por la sal extra en la herida - la serie original no es estacionaria de todos modos.
2) Esta probabilidad es casi siempre distinta de cero.
3. ¿Ha comprobado la multicolinealidad? En mi opinión, si se elimina la multicolinealidad, sólo queda una variable. ¿Ha determinado los factores significativos?
4. ¿Cuántas observaciones tienes para 5 variables?
¿Cómo es que eres tan culto?
1. perdón por la sal extra en la herida - la serie original no es estacionaria de todos modos.
Por supuesto, no nos interesan los demás.
2. Esa probabilidad es casi siempre distinta de cero.
No es cierto. Si es distinto de cero, es un error de forma funcional.
3. ¿Ha comprobado la multicolinealidad? En mi opinión, si se elimina la multicolinealidad, sólo queda una variable. ¿Ha identificado los factores significativos?
Lo que son "factores significativos" no lo entiendo, pero por favor, mira los coeficientes de correlación.
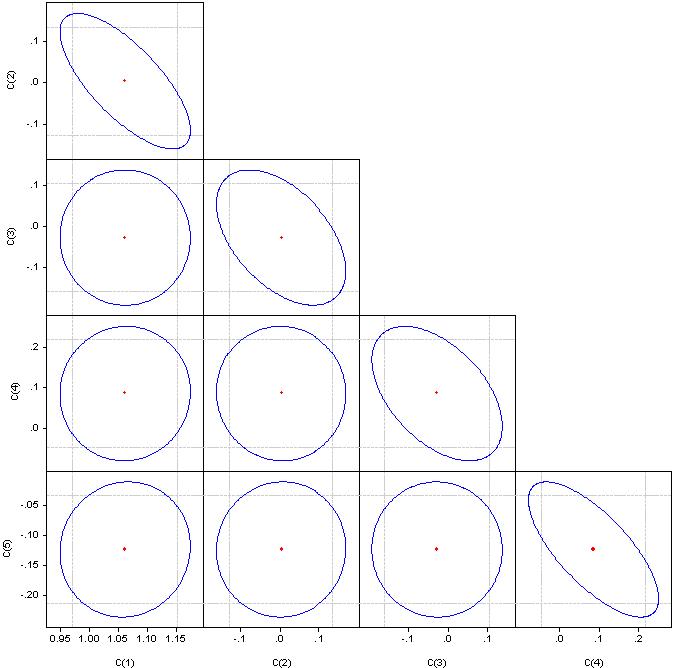
Si es un círculo, la correlación es cero. Si se fusionan en una línea recta, la correlación entre el par de coeficientes correspondiente es del 100%.
4. ¿Cuántas observaciones tienes para 5 variables?
6736 observaciones
El primer paso en cualquier modelo de regresión es la selección de factores. Si no se aplica la regresión por pasos (con inclusiones o excepciones), hay que seleccionarlas manualmente.
Multicolinealidad - dependencia estrecha entre las variables de factores incluidas en el modelo. No la correlación de los coeficientes, sino la correlación de los factores.
La presencia de multicolinealidad conduce a:
- distorsión del valor de los parámetros del modelo, que tienden a sobreestimar;
- condicionamiento débil del sistema de ecuaciones normales;
- complicación de el proceso de determinar las característicasmás significativas del factor .
Un indicador de multicolinealidad es que los coeficientes de correlación por pares superan el valor de 0,8. Aquí los factores tienen claramente una fuerte correlación. Para eliminarlo hay que suprimir los factores redundantes. Ya sea manualmente o por regresión escalonada.
Busque en el paquete - regresión por pasos o regresión por crestas.
Y 6736/4 son demasiadas observaciones. Hay que buscar en Google, no recuerdo cómo determinar el número óptimo de observaciones en función del número de factores.
Tengan la amabilidad de participar en mis hilos de econometría.
Sigamos con la selección de literatura.
El siguiente tema es el de los rezagos de Almon.
Como se ha señalado anteriormente, existen dificultades con los coeficientes de regresión calculados mediante el método de los mínimos cuadrados. Ha surgido la idea de imponer restricciones adicionales a los coeficientes de regresión en los que la variable dependiente está determinada por varios rezagos de la variable independiente, como en la ecuación anterior.
La idea es imponer restricciones a los coeficientes en los valores de los rezagos de manera que obedezcan a alguna distribución polinómica. EViews llama a este enfoque "polinomios de retardo distribuido (PDL)". La elección del grado concreto del polinomio se determina experimentalmente.
Este enfoque se describe aquí.
He aquí un ejemplo práctico.
Construyamos un análogo de una escala con un periodo de 5, pero los coeficientes de la barra deben estar en un polinomio de 3er orden.
En EViews se escribe como sigue para el EURUSD
EURUSD PDL(EURUSD(-1), 5,3)
En una forma más familiar:
EURUSD = + C(5)*EURUSD(-1) + C(6)*EURUSD(-2) + C(7)*EURUSD(-3) + C(8)*EURUSD(-4) + C(9)*EURUSD(-5) + C(10)*EURUSD(-6)
Estimamos los coeficientes por MCO y obtenemos el resultado de la estimación de los coeficientes:
EURUSD = + 0,934972661616*EURUSD(-1) + 0,139869148138*EURUSD(-2) - 0,093599954464*EURUSD(-3) - 0,0264992987207*EURUSD(-4) + 0,0801064628352*EURUSD(-5) - 0,0348473223286*EURUSD(-6)
La estadística de la estimación de la ecuación es la siguiente:
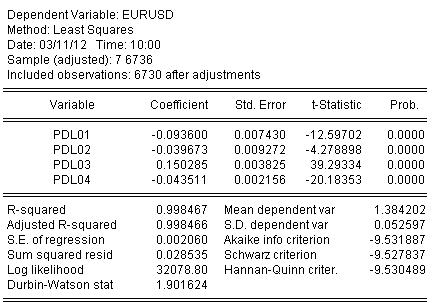
A partir de las estadísticas podemos ver un muy buen nivel de mapeo del cociente inicial por nuestra ondulación de Almon R-cuadrado = 0,998467
Gráficamente se ve así:

La regresión (la ondulación de Almon) ha cubierto completamente el cociente original.
Y una última cucharada de miel.
Veamos cuál es el residuo, es decir, la diferencia entre nuestro puré de Almon y el cotier original. La estacionariedad/no estacionariedad de este residuo es muy importante.

La prueba de la raíz unitaria indica que el residuo es estacionario.
Los mash-ups que utilizamos no tienen este nivel de ajuste al cociente original ni la propiedad de estacionariedad del error de ajuste.
Me gustaría trasladar los enlaces de un hilo vecino.
Estos enlaces se refieren al área más problemática: el pronóstico.
El primero es un archivo adjunto. Hay una lista de referencias.
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Si se busca en Google la palabra "econometría", se obtiene una enorme lista de literatura, difícil de entender incluso para un experto. Un libro dice una cosa, otro - otra, el tercero - sólo una recopilación de los dos primeros con algunas inexactitudes. Pero el enfoque "de los libros" no combina la claridad de la aplicación de estos libros en la práctica. No me interesa que los intelectuales desciendan a tonterías de empollón.
Al igual que otras listas de libros en este foro, por ejemplo, sobre estadística, propongo que recopilemos colectivamente una lista de libros de texto, monografías, disertaciones, artículos, recursos de Internet y paquetes de software que, en opinión de los participantes, sean relevantes para la medición de datos económicos - para la econometría. Sin embargo, no olvidemos que la estadística matemática es la hermana mayor de la econometría. Sugiero no incluir en esta lista nada relacionado con el análisis técnico.
Para excluir el deslizamiento hacia la botánica, propongo un enfoque específico de la lista de libros. Publicamos enlaces (libros en sí) sólo si sé software, que implementa los algoritmos de estos libros. Lo he reducido a EViews. Este programa no tiene ninguna ventaja sobre otros, tiene ventajas y desventajas, pero lo tomo como un rubricador de la econometría. He adjuntado el índice del segundo volumen del manual de usuario, para poder esbozar de una vez el mayor número posible de problemas. Debido al enfoque propuesto, se excluyen varias áreas utilizadas en econometría, pero no incluidas en EVIEWS, por ejemplo, NS, wavelets, etc. Naturalmente, las referencias a estos programas y libros también son bienvenidas.
Si no sólo podemos proporcionar un enlace a la fuente del algoritmo, sino también hacer cálculos específicos, este hilo no tendrá ningún valor.
Sugiero utilizar los números de los capítulos del anexo para agrupar los libros.
Así que, por favor, apoyen.