[Archivo] Matemáticas puras, física, química, etc.: problemas de entrenamiento cerebral no relacionados con el comercio de ninguna manera - página 267
Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
Es decir, no puedes sacar dos bolas, está prohibido.
MaStak, estás siendo demagógico en este momento. Sabes perfectamente que la cuestión es cuántas veces tenemos que sacar el balón.
MaStak, ну ты ж ведь сейчас демагогией занимаешься.
Estaba buscando el truco en la condición - lo encontré )
Bien, mañana muéstrame la solución que tienes. No importa cuántas veces lo saques. Y entre todos intentaremos optimizarlo. Me voy a la cama, tengo que levantarme temprano.
Era:
xx yy xy // Contenido
xx yy xy // InscripciónSe convirtió:
** ** *y // Contenidoxy xx yy // Inscripciones
Uno de ellos se ha sacado y ha descubierto que es "y", y la pregunta es "¿y qué?", ahora lo sabemos todo sobre todos ellos )
En palabras del clásico: "- Esta información no me basta."
Было:
xx yy xy // Содержимое
xx yy xy // НадписиСтало:
** ** *y // Содержимоеxy xx yy // Надписи
Один как бы вытащили и узнали что это "y", и спрашивается "и чё ?", теперь известно всё о всех )
Говоря словами классика: "- Этой информации мне недостаточно."
Suficiente. El enunciado del problema lo dice todo: "Cada caja está etiquetada con una inscripción que no coincide con el contenido".
Достаточно. в условии задачи все сказано "на каждой коробке стоит надпись, не соответствующая содержимому"
xy xx yy // Inscripción
---------
xx yy xy
yy xy xx
---------
Sí, efectivamente, 1 bola de xy )
Tengo 2 soluciones más ;D
La primera y la última (a y c) no tienen solución. La segunda, sin embargo, tiene solución:
¡!
Haz clic:
cinco veces en el azul,
una vez en la roja,
el verde izquierdo una vez,
el del medio 2 veces,
el derecho 3 veces.
Al problema sobre el avión y el cohete. No sé quién compone los problemas y sus soluciones, pero...
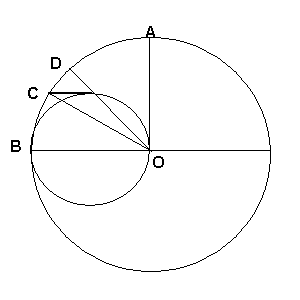
Si después de volar la mitad del camino el cohete está en el centro del semicírculo pequeño, y el avión está en el centro del cuarto de círculo grande,Entonces la tangente al semicírculo pequeño debe unir estos dos puntos (según la solución dada).
Sin embargo, este no es el caso, lo que demuestra inmediatamente la incorrección de la solución.
¡Nos engañan, señores!