¡Nuestra Masha! - página 2
Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
Un alto nivel de alisamiento tampoco es un buen resultado: un aumento de la rentabilidad. Aumentar la suavidad supondrá, en cualquier caso, un aumento de la latencia. Pero incluso suponiendo que tengamos un retraso cero, el aumento de la suavidad hará que se salten las operaciones más pequeñas, lo que disminuirá la cantidad de operaciones y, respectivamente, el beneficio y, por lo tanto, aumentará la reducción.....
Incluso en el gráfico se puede ver claramente que una parte de las operaciones bastante grandes, que teóricamente podrían haber sido tomadas, no han sido tomadas, por lo tanto, el beneficio ha disminuido.....
Un alto nivel de alisamiento tampoco es bueno para aumentar los beneficios. Aumentar la suavidad supondrá, en cualquier caso, un aumento de la latencia. Pero incluso si suponemos que tenemos un retardo cero, el aumento del alisamiento conducirá a la omisión de las operaciones más pequeñas y, en consecuencia, a la disminución de las operaciones, respectivamente, la disminución de los beneficios y el aumento de las detracciones.....
Ajustarse de forma adaptativa a la mejor variante.
>> El caso que describes es el problema de todos los indicadores dependientes del tiempo. Suprimir el tiempo en el sentido clásico y utilizar otros métodos.
Hace tiempo que he abandonado este tipo de CTs y uso otros métodos....Sólo escribí el post como una opinión sobre lo que el aumento de la suavidad puede llevar a )))))
Hace tiempo que abandoné este tipo de CTs y uso otros métodos....Sólo escribí un post a modo de opinión sobre lo que puede suponer el aumento de la suavidad )))))
¿Puedo escribirte una carta?
Además, a todo esto hay que sumarle los errores (pérdidas) por aumentar el retraso (no hay que ser altruista) y la cuestión del beneficio puede quedar en el aire .....))))
Estoy dispuesto a discutir sobre la autoría de la idea. Lo más probable es que la idea sea tan antigua como la AM. :))
Y, en general, el tema me resulta interesante: yo mismo me dedico a ello. Naturalmente, no todo es tan bonito como en su dibujo. Está claro que le faltan muchas flechas.
Ahora en orden:
En mi opinión, un sistema de este tipo no dará beneficios sin un MM agresivo.
¡Bueno, camarada! - Así que vamos por el buen camino.
La figura muestra una ilustración muy esquemática del método de apertura/cierre de posiciones.
El argumento es discutible (igualdad de la segunda derivada a cero), por lo que requiere un argumento de su parte. En cuanto al extremo (igualdad a cero de la primera derivada), parece que no hace falta argumentar.
La exigencia de la cercanía de la MA a la cotización y la exigencia simultánea de su suavidad no entran (ni pueden entrar) en conflicto, sino que se complementan. Un ejemplo llamativo es la habitual EMA media exponencial. Su forma recursiva se obtiene precisamente de la minimización del funcional, que requiere proximidad y suavidad simultáneamente.
3. Esto puede considerarse un desarrollo del método. Para empezar, hay que obtener una solución para los requisitos obvios de la forma del funcional.
Swetten escribió >>
Disculpe, ¿qué es FZ?
FZ - retardo de fase. Un término del DSP.
TheXpert 19.01.2009 14:45
¿La función de destino se basa en la referencia al esquema?
Un alisamiento excesivo no nos dará un buen resultado, sino que aumentará el beneficio. El aumento de la suavidad conducirá en cualquier caso a un aumento del retraso. Pero incluso si suponemos que tenemos un retardo cero, el aumento del alisamiento conducirá a la omisión de las operaciones más pequeñas y, en consecuencia, a la disminución de las operaciones, respectivamente, a la disminución del beneficio y al aumento del drawdown.....
¿Tal vez probarlo secuencialmente?
Haz una primera variante, analízala.
Como esto y lo otro, no me gusta, así que quitaremos esto y lo otro y lo haremos.
Es que veo que hay mucha confusión, y la idea original era genial.
¿Debemos intentarlo secuencialmente?
Haz una versión inicial, analízala.
Nos gusta esto y lo otro, no nos gusta lo otro, así que quitamos esto y lo otro, y nos hacemos un lío.
Es que veo mucha confusión aquí, y la idea original era genial.
No hay ningún lío.
Si no hay nada más, recordemos los requisitos básicos para un MA perfecto:
1. proximidad a la RV original. Este requisito es igual a la pequeñez de la distancia entre el cociente X (línea verde en la imagen) y la curva suavizada Y (azul). Se puede escribir que en promedio, sobre una muestra grande, debe satisfacer: (X[i]-Y[i])^2-->min
2. Suavidad de MA. Este requisito es igual a la pequeñez de la distancia entre muestras vecinas de la curva suave: (Y[i]-Y[i-1])^2-->min.
3. La curva de Equidad que se compondrá de los trozos picados de la BP inicial considerando la dirección (signo) de las posiciones abiertas (entre líneas verticales en la imagen) debe ser creciente. El signo de la apertura de la posición es igual al signo de la derivada de la MA. En nuestra terminología, sign(Y[i]-Y[i-1]). En este caso, la curva de equidad estará compuesta por piezas de kotier que se unirán a tope según el signo de la posición a cerrar. Así es como se puede aplicar. Construyamos una serie de primera diferencia (FDD) d[i]=X[i]-X[i-1] para el kotier: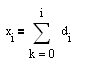
, entonces un crecimiento rápido de la curva de equidad (
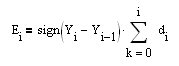), equivale a la exigencia de maximizar la primera derivada de la misma: dE[i]/dt=E[i]-E[i-1]= signo(Y[i]-Y[i-1])*(X[i]-X[i-1]) o con un tramo pequeño, pero aceptable, en nuestro caso, {(Y[i]-Y[i-1])*(X[i]-X[i-1])}^2-->max Es obvio que la maximización de alguna expresión es igual a su minimización con signo contrario:-{(Y[i]-Y[i-1])*(Х[i]-Х[i-1])}^2-->min.
Eso es todo. Obtenemos el funcional requerido para la minimización:
S=w1*(X-Y)^2+w2*(Y[i]-Y[i-1])^2-w3*{(Y[i]-Y[i-1])*(Х[i]-Х[i-1])}^2-->min
Necesitamos encontrar su mínimo relativo a Y[i], donde i es el dato actual.
¡No hay dispersión!
Si no hay más deseos, refresquemos la memoria sobre los requisitos básicos para un MA perfecto:
En mi opinión, falta la vista de la función Y. ¿O me he perdido algo?
Estupendo, he encontrado una solución de este tipo para un periodo de tiempo. ¿Y luego qué?
¿Cómo qué? Ganamos... la rentabilidad se invierte en la función objetivo.