Discusión sobre el artículo "Cómo crear gráficos 3D en DirectX en MetaTrader 5"
Wow! No sabía que se podía lograr eso en mql5. Yo he modelado en 3d con otros fines pero no sabía que aquí se podía también.
Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
Artículo publicado Cómo crear gráficos 3D en DirectX en MetaTrader 5:
Los gráficos en 3D resultan de gran ayuda a la hora de analizar grandes volúmenes de datos, ya que permiten visualizar regularidades ocultas. Estas tareas también se pueden resolver directamente en MQL5: las funciones de trabajo con DireсtX permiten MetaTrader 5. Comience el estudio dibujando figuras de volumen sencillas.
Al principio, cuando las computadoras y las tarjetas gráficas no eran tan potentes como ahora, cada polígono se dividía en triángulos, dado que, con la ayuda de un triángulo, se puede describir de forma unívoca la posición de una pequeña área de la superficie y calcular sobre ella parámetros tan necesarios como la iluminación y el reflejo de la luz incidente. Un conjunto de varios de estos pequeños triángulos permite crear una imagen realista en tres dimensiones de un objeto. Aquí y en lo sucesivo, triángulo y polígono van a actuar como sinónimos, ya que representar un triángulo resulta bastante más sencillo que representar un polígono con N vértices.
Cubo compuesto por triángulos.
De esta forma, para crear un modelo tridimensional de un objeto, basta con describir las coordenadas de cada vértice del triángulo, para después calcular las coordenadas de cada punto del objeto, incluso si el propio objeto se desplaza en el espacio o cambia la posición del observador. Los picos del triángulo se llaman vértices (vertex), los segmentos que los unen se llaman bordes (edge), y la superficie confinada entre los segmentos se llama cara (face). Conociendo la ubicación de un triángulo en el espacio, podremos construir el vector normal (el vector que parte desde la superficie y es perpendicular a la misma) con respecto al mismo según las leyes del álgebra lineal, y calcular de esta forma cómo la luz que incide en la cara procedente de una fuente coloreará la superficie y se reflejará en ella.
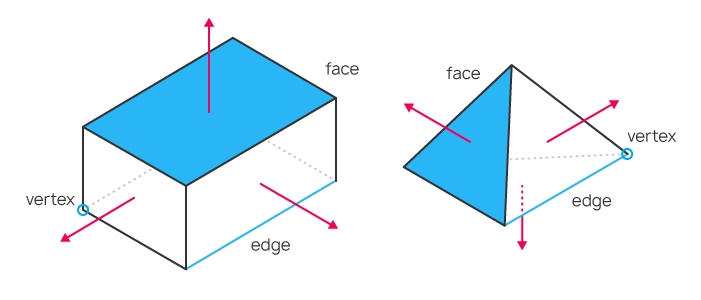
Ejemplos de objetos sencillos con vértices, bordes, caras y vectores normales. El vector normal es la flecha de color rojo.Autor: MetaQuotes