PreCogniTrade
- Indicators
- Juan Manuel Rojas Perez
- Version: 1.0
PreCogniTrade: Un Indicador Técnico Avanzado para Predecir el Mercado (Fase Beta)
El PreCogniTrade es un indicador técnico revolucionario diseñado para los traders que buscan una ventaja competitiva en los mercados financieros. Este indicador no solo analiza las tendencias actuales, sino que también predice los movimientos futuros de los precios con una precisión asombrosa, lo que lo convierte en una herramienta de incalculable valor para cualquier estrategia de trading.
Características Principales:
- Predicción de Movimientos Futuros: Utiliza algoritmos complejos y análisis predictivo para anticipar los movimientos del mercado antes de que sucedan.
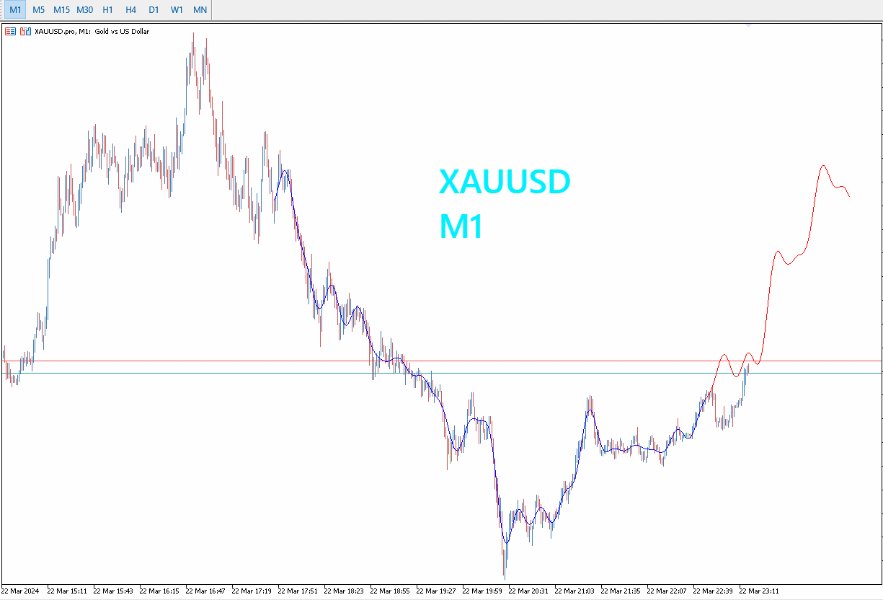
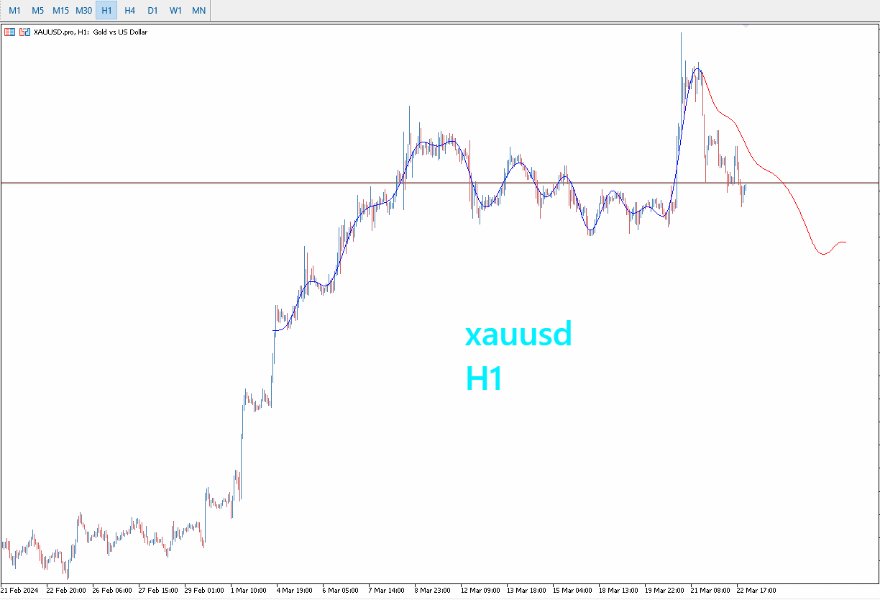
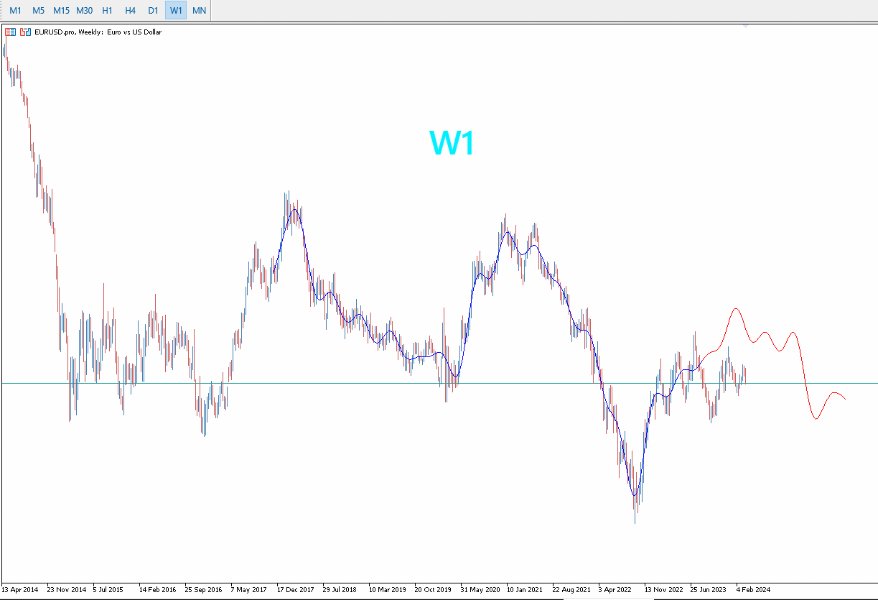
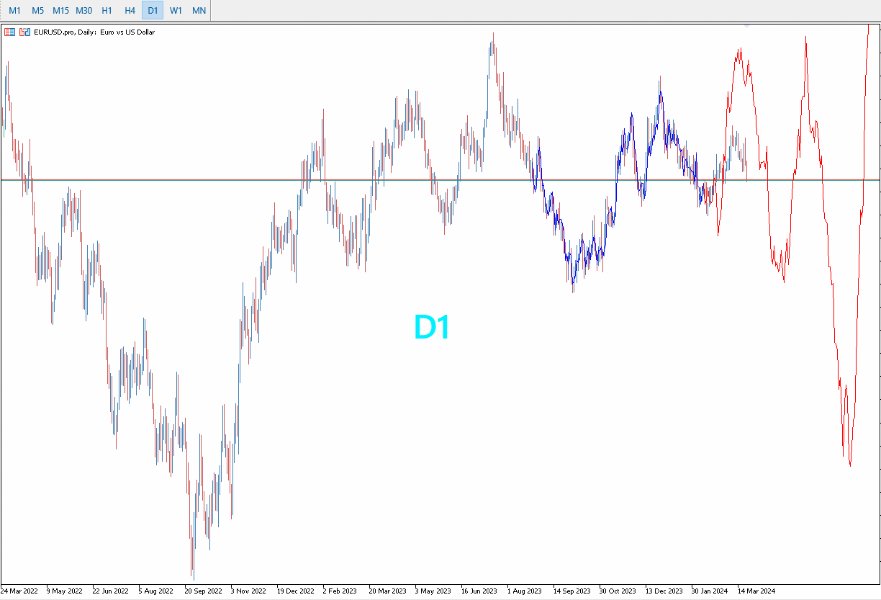
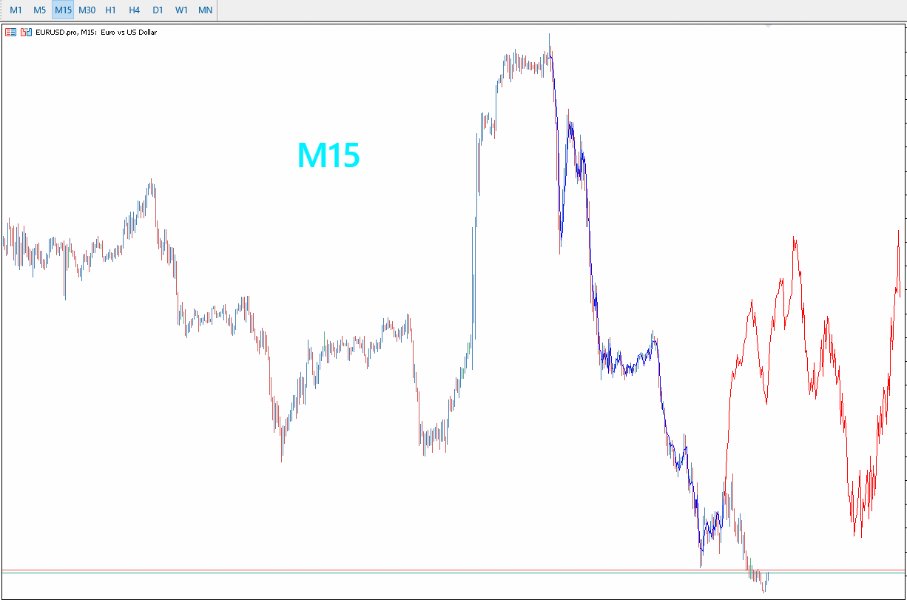
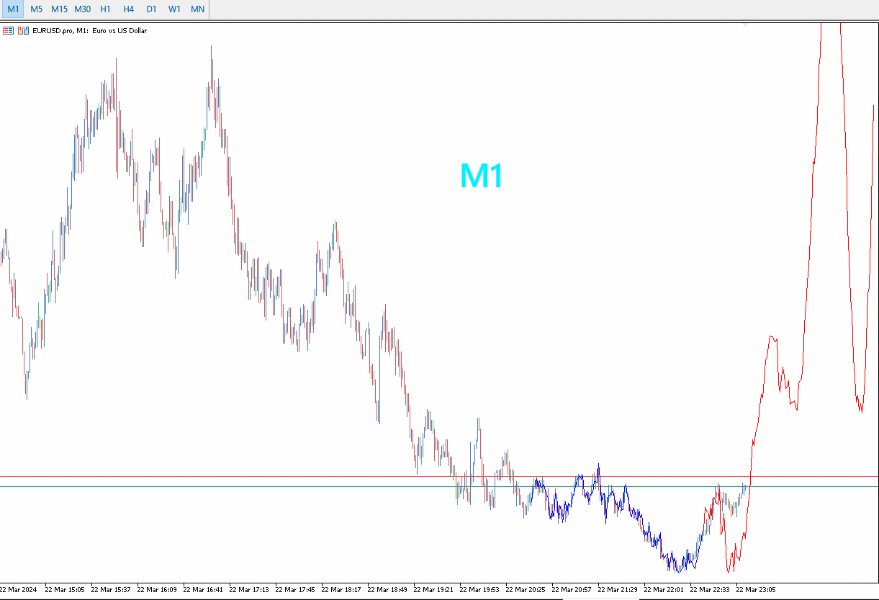
- Optimizado para Marcos Temporales Mayores: El PreCogniTrade brilla especialmente en marcos temporales más amplios, donde las predicciones son más estables y confiables.
- Visualización Dinámica: Dibuja el probable movimiento del precio con sus impulsos y retrocesos, permitiendo a los traders visualizar y planificar sus operaciones con mayor claridad.
- Fórmulas Complejas: De todos los indicadores en mi arsenal, el PreCogniTrade contiene las fórmulas más complejas, integrando una variedad de factores técnicos y cuantitativos para una predicción precisa.
La importancia del PreCogniTrade radica en su capacidad para proporcionar a los traders una visión profunda del comportamiento futuro del mercado, permitiéndoles tomar decisiones informadas y proactivas. Con este indicador, los traders pueden ajustar sus estrategias para alinearse con los movimientos anticipados del mercado, maximizando así sus oportunidades de éxito y minimizando los riesgos.
En resumen, el PreCogniTrade es una herramienta esencial que transforma la forma en que los traders interactúan con los mercados financieros, ofreciendo una perspectiva única que va más allá del análisis técnico tradicional. Su implementación en marcos temporales mayores asegura que los traders puedan confiar en sus señales para tomar decisiones de trading más inteligentes y rentables.
Métodos Usados en el Indicador
El método de extrapolación es una técnica estadística utilizada para estimar valores futuros o desconocidos basándose en datos conocidos. Es particularmente útil en análisis de series temporales y análisis geoespacial debido a su capacidad para considerar el impacto de factores temporales y espaciales en los datos.
¿Cómo funciona la extrapolación?
La extrapolación se realiza extendiendo una secuencia conocida de valores más allá del rango observado. Por ejemplo, si tienes datos de ventas de los últimos dos años, podrías usar la extrapolación para predecir las ventas del próximo año.
Métodos Comunes de Extrapolación:
- Extrapolación Lineal: Utiliza una ecuación lineal para predecir resultados futuros. Es adecuada para predicciones cercanas a los datos conocidos.
- Extrapolación Polinómica: Emplea una ecuación polinómica para hacer predicciones. Se utiliza cuando los puntos de datos muestran una tendencia no lineal y puede ofrecer predicciones más precisas.
Es importante tener en cuenta que la extrapolación conlleva incertidumbre y riesgos, ya que se basa en la suposición de que las tendencias pasadas continuarán en el futuro. Por lo tanto, los resultados deben ser interpretados con cautela y es recomendable utilizar la extrapolación junto con otras técnicas de análisis y consideraciones contextuales.
El método de autocorrelación es una técnica estadística que mide la correlación de una señal consigo misma a través de diferentes intervalos de tiempo. Es decir, evalúa la similitud entre observaciones de una variable en función del desfase temporal entre ellas.
¿Cómo funciona la autocorrelación? La autocorrelación compara una señal con una copia retrasada de sí misma para identificar patrones repetitivos o la presencia de una señal periódica que puede estar oculta por el ruido. También se utiliza para identificar la frecuencia fundamental que falta en una señal, implicada por sus frecuencias armónicas.
Aplicaciones de la Autocorrelación:
Análisis de Series Temporales: En el análisis de series temporales, la autocorrelación puede revelar patrones periódicos y tendencias en los datos.
Procesamiento de Señales: En el procesamiento de señales, se utiliza para analizar funciones o series de valores, como señales en el dominio del tiempo.
Modelos ARMA y ARIMA: En econometría, la autocorrelación es un componente clave de los modelos autoregresivos de media móvil (ARMA) y autoregresivos integrados de media móvil (ARIMA), que son utilizados para el análisis y la predicción de datos económicos.
La autocorrelación puede ser positiva o negativa y su valor varía entre -1 y 1. Una autocorrelación positiva indica que un aumento observado en un intervalo de tiempo tiende a ser seguido por un aumento en el intervalo de tiempo retrasado. Por otro lado, una autocorrelación negativa sugiere que un aumento es seguido por una disminución.
Es importante recordar que la autocorrelación es solo una herramienta de análisis y debe usarse junto con otros métodos para obtener una comprensión más completa de los datos.
El método Weighted Burg es una técnica avanzada en el análisis espectral, que forma parte de los métodos de estimación autoregresiva (AR). Esta técnica se utiliza para mejorar la estimación del espectro de una señal, especialmente cuando se trabaja con datos limitados o ruidosos.
Características del método Weighted Burg:
- Minimización de Errores Predictivos: Estima los coeficientes AR minimizando una medida ponderada de los errores predictivos lineales hacia adelante y hacia atrás.
- Ponderaciones Data-Adaptativas: Utiliza pesos que son proporcionales a la energía común de las realizaciones del proceso hacia adelante y hacia atrás, lo que resulta en una representación de filtro estable.
- Mejora del Rendimiento Espectral: Comparado con otras técnicas de Burg ponderadas, el método Weighted Burg demuestra mejoras en el sesgo de frecuencia y la resolución.
Este método es particularmente útil en campos como el procesamiento de señales y la econometría, donde se requiere una estimación precisa del espectro para analizar y predecir comportamientos futuros basados en datos históricos. Aunque es una herramienta poderosa, es importante utilizarla junto con otras técnicas de análisis para obtener resultados más robustos y confiables.
El método de Burg con funciones de ponderación de Helme-Nikkias es una variante avanzada del método de Burg tradicional, utilizado para la estimación espectral de potencia. Este enfoque combina el método de Burg, que es conocido por su alta resolución en registros de datos cortos y por producir siempre un modelo estable, con funciones de ponderación de Helme-Nikkias para mejorar la precisión de la estimación espectral.
El método de Burg tradicional ajusta un modelo autoregresivo (AR) a la señal minimizando los errores de predicción hacia adelante y hacia atrás en el sentido de mínimos cuadrados. Las funciones de ponderación de Helme-Nikkias se aplican para dar diferentes pesos a los datos en el proceso de ajuste del modelo AR, lo que puede ser particularmente útil cuando se trata con señales que tienen características no estacionarias o cuando se desea enfatizar ciertas partes de la señal sobre otras.
La combinación de estas técnicas permite obtener una estimación espectral más robusta y precisa, lo que es beneficioso en aplicaciones como el análisis de señales y el procesamiento de datos en tiempo real. Sin embargo, es importante tener en cuenta que, como con cualquier método de estimación, los resultados deben interpretarse con cuidado y en el contexto de la señal y el ruido presentes en los datos.
El método Itakura-Saito, también conocido como la distancia Itakura-Saito, es una técnica utilizada para medir la diferencia entre un espectro original y una aproximación de ese espectro. Aunque no es una medida perceptual, está diseñada para reflejar la (dis)similitud perceptual. Fue propuesto por Fumitada Itakura y Shuzo Saito en la década de 1960.
La distancia Itakura-Saito se define como una divergencia de Bregman generada por la función logarítmica negativa, pero no es una métrica verdadera ya que no es simétrica y no cumple con la desigualdad triangular. En el contexto de la factorización de matrices no negativas, la divergencia de Itakura-Saito se puede utilizar como una medida de la calidad de la factorización, lo que implica un modelo estadístico significativo de los componentes y puede resolverse a través de un método iterativo.
Este método es particularmente útil en el análisis espectral y ha sido ampliamente utilizado en aplicaciones como el procesamiento de señales y el análisis de datos en tiempo real. La elección de utilizar la distancia Itakura-Saito en lugar de otras medidas se basa en su capacidad para proporcionar una estimación más precisa del espectro, especialmente en situaciones donde los datos pueden ser limitados o estar contaminados con ruido.
El método de covarianza modificado es una técnica de estimación espectral que se utiliza para analizar la densidad espectral de potencia (PSD) de una señal. Este método ajusta un modelo autoregresivo (AR) a la señal minimizando los errores de predicción hacia adelante y hacia atrás en el sentido de mínimos cuadrados.
Características principales del método de covarianza modificado:
- Estimación AR: Ajusta un modelo autoregresivo al minimizar los errores de predicción.
- Minimización de Errores: Minimiza los errores de predicción hacia adelante y hacia atrás.
- Estabilidad del Modelo: Siempre produce un modelo estable, lo que es crucial para la fiabilidad de la estimación espectral.
- Alta Resolución: Ofrece una alta resolución para registros de datos cortos, lo que es beneficioso en situaciones donde los datos son limitados.
Este método es ampliamente utilizado en el procesamiento de señales y en el análisis de datos en tiempo real, proporcionando una herramienta robusta para la estimación espectral de potencia en diversas aplicaciones.