I can't get through the maze of code, but I would like to compare it.
Initial quote
We have the following smoothing variants:
Smoothing result
Regression equation:
eurusd = c(1)*eurusdsm(-1) + c(2)*trend + c(3)
Estimation of the regression equation
| Variable | Coefficient | Stand.osh. | t-statistic | probability |
| EURUSDSM(-1) | 0.759607 | 0.049127 | 15.46225 | 0.0000 |
| REND | 0.000207 | 5.79E-05 | 3.577804 | 0.0005 |
| C | 0.314884 | 0.065276 | 4.823886 | 0.0000 |
R-squared = 0.788273
Standard error of regression = 0.015172
From the figures obtained, we note:
all regression coefficients are significant (the probability of their equality to zero is equal to zero)
rather high (but not very high) R-square, which says that regression explains 78% of the variance
the standard error is 151 pips. That's a huge figure.
Can we trust the resulting numbers?
I wouldn't, since according to Jarque-Bera the probability that the smoothed series has a normal distribution is 31%.
Let's make a forecast:
The forecast error is not far behind the regression error and exceeds 100 pips
Let's look at the graph of the forecast error:
Well, this is a complete finish: the error is variable, which means that the future behaviour of the forecast is unknown!
To find out the reason, let's look at the correlation of the coefficients of the regression equation:
We can consider that the coefficients c(1) and c(3) are almost 100% correlated.
My conclusion is that we cannot use exponential smoothing for prediction.
Why do we have different results?
It is obvious to me that the optimal parameters you have found are nothing more than a trivial fitting. The regression itself is hopeless, its coefficients are correlated.
It is obvious to me that the optimal parameters you have found are nothing more than a trivial fitting. The regression itself is hopeless, the coefficients in it are correlated.
Thank you for your interest in the article.
Please clarify what you meant? What results do not converge and what are the optimal parameters?
Please clarify what you meant by that?
Pardon me, you say you can use it, but my conclusion is that you can't.
What to use and why?
In conclusion, it should be noted that exponential smoothing models in certain cases are able to provide forecasts that are as accurate as forecasts obtained using more complex models, thus once again confirming the fact that the most complex model is not always the best.
My conclusion is that exponential smoothing should not be used for forecasting.
What are your questions and why do you ask them?
My conclusion is that you can't use exponential smoothing for forecasting.
What are your questions about and what are they for?
I would love to try to answer something, but I need to know the question at least. Otherwise I will have to guess and fantasise.
I'll try to clarify again.
Exponential smoothing models cannot be used to forecast eurusd pair, any quotes or never at all?
P.S..
You have in your text: "Regression equation:eurusd = c(1)*eurusdsm(-1) + c(2)*trend + c(3)". Why regression, the article is about exponential smoothing models, and there is a different model, instead of c(3) there is a random variable with some distribution and dispersion?
In your text: "Regression equation:eurusd = c(1)*eurusdsm(-1) + c(2)*trend + c(3)". Why regression, the article is about exponential smoothing models, and there is a different model, there instead of c(3) is a random variable with some distribution and variance?
It doesn't work, talking blind man to deaf man. Let's postpone it.
Congratulations again on a good article.
It's not working, talking blind man to deaf man. Let's postpone it.
Congratulations again on a good article.
I am actually very curious about your point of view on forecasting using exponential smoothing. There are many things I just don't know and I am always happy to try to discover something new at every opportunity, that's why I am asking questions.
If it is not too much trouble, please explain why if the distribution of the original sequence (or smoothed original sequence) is not normal, the forecast cannot be trusted? Or did I misunderstand you?
Thanks for the congratulations.
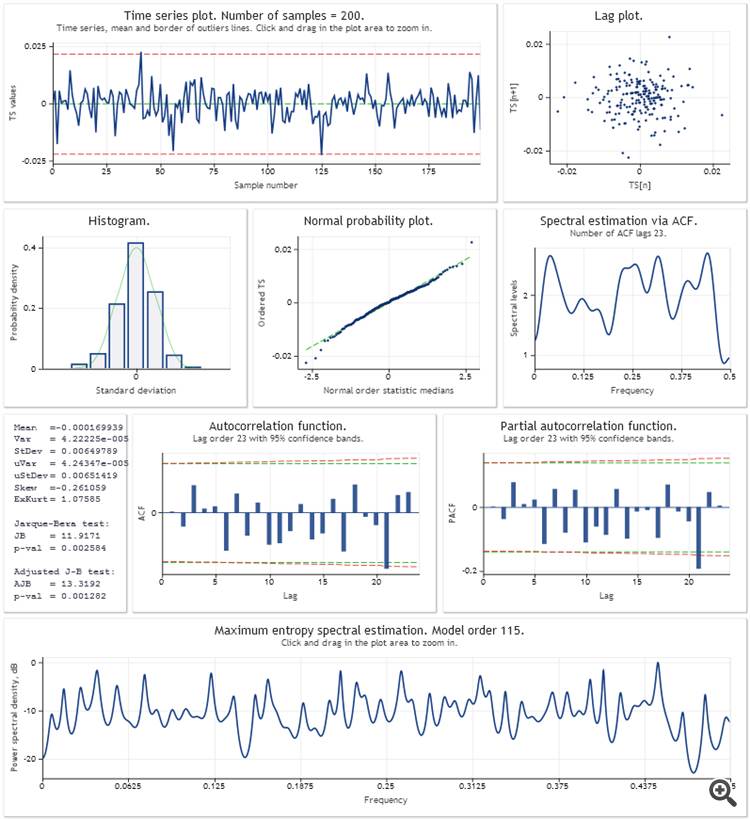
Here is a one step ahead prediction error analysis for the additive linear growth model with damping. The model parameters were optimised using a sample of the last 200 values of USDJPY,M1. In the same way as in the Optimisation_Test.mq5 script from the article.
https:// www.mql5.com/ru/articles/292
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
New article Time Series Forecasting Using Exponential Smoothing is published:
The article familiarizes the reader with exponential smoothing models used for short-term forecasting of time series. In addition, it touches upon the issues related to optimization and estimation of the forecast results and provides a few examples of scripts and indicators. This article will be useful as a first acquaintance with principles of forecasting on the basis of exponential smoothing models.
Author: Victor