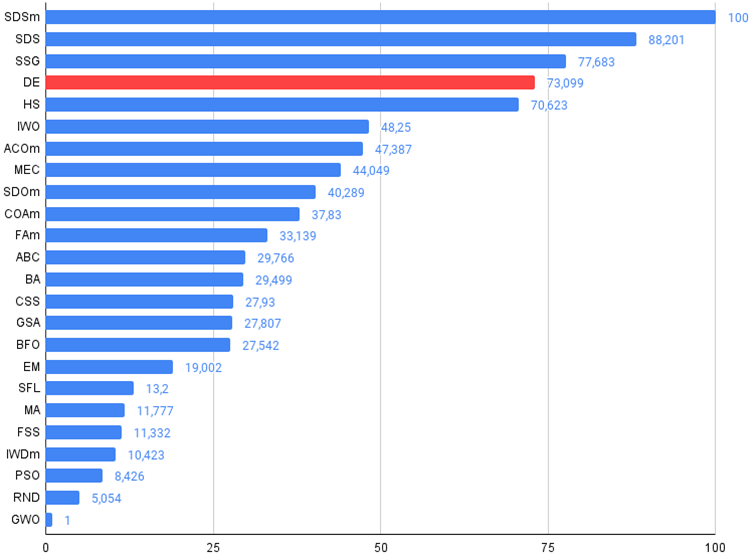
Please add links to the description of each algorithm in order as in the diagram.
Thanks again for sharing.
fxsaber #:
Please add links to the description of each algorithm in the order as in the diagram.
Thanks again for sharing.
Thanks for the suggestion.
It would be great if you could make the links directly on the bar chart, but unfortunately the article engine doesn't allow that.
Links can be added in the table, I think. I'll try to do it.
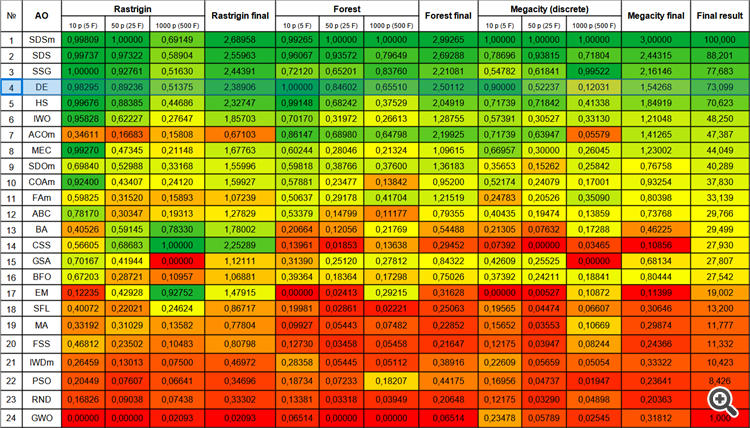
I made a mistake, the coloured table picture from the previous article, replaced it with the current one.
After checking the latest version of the article the new picture will be available. However, there is an actual coloured table in the archive and you can look at it.
Here it is:
You are missing trading opportunities:
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
Registration
Log in
You agree to website policy and terms of use
If you do not have an account, please register
Check out the new article: Population optimization algorithms: Differential Evolution (DE).
In this article, we will consider the algorithm that demonstrates the most controversial results of all those discussed previously - the differential evolution (DE) algorithm.
The idea of differential evolution is a combination of simplicity and efficiency. The differential evolution algorithm uses a population of vectors representing potential solutions. Each vector consists of components that represent the values of the optimization problem variables.
In DE, a vector takes the role of the search agent. The algorithm starts by creating a random population of vectors. An iterative process then occurs, in which each vector mutates and crosses with other vectors in the population. Mutation is accomplished by adding the difference between two randomly selected vectors from the population to a third vector. This creates a new vector that represents a potential solution to the problem.
After mutation, the mutated vector is crossed with the original vector. Crossing allows combining information from two vectors and creating new solutions. The obtained result is compared with the current best solution in the population. If the new vector is better, it replaces the old one and becomes part of the population. Mutation allows exploring the search space, while crossing allows combining information from different vectors and creating new solutions.
Mutation, crossbreeding and replacement are repeated over several iterations until a stop condition is reached, such as a given number of iterations or reaching the required solution accuracy (in our case, reaching 10,000 fitness function runs).
Author: Andrey Dik