A school warm-up exercise to occupy your time - page 7

New comment
 
Nikolai Semko:
Is it?
Not at the computer at the moment.
I think I've tried it. ME didn't recognise this function and didn't find it in help by F1
My understanding is that it is an AlgLib library

https://www.mql5.com/ru/docs/standardlibrary/mathematics/stat/mathsubfunctions/statmathsum

 
Aleksey Nikolayev:

https://www.mql5.com/ru/docs/standardlibrary/mathematics/stat/mathsubfunctions/statmathsum

Yeah. Implementation ...

It's a lib, it's supposed to go like this:

1. At zero array returns value initialized by default constructor (for primitives it's 0)

template<typename T>
T MathSum(const T &arr[]){
   T sum=T();
   for (int i=0,size=ArraySize(arr);i<size;sum+=arr[i++]);
   return sum;
}

2. At zero array, it crashes in runtime.

template<typename T>
T MathSum(const T &arr[]){
   T sum=arr[0];
   for (int i=1,size=ArraySize(arr);i<size;sum+=arr[i++]);
   return sum;
}

3. Returns a structure containing the result code and amount

template<typename T>
struct SRet{
   int retCode; //0 - Ок, -1 - Not initialized
   T res;
   SRet():retCode(-1){}
   SRet(uint code,const T &_res):retCode(code),res(_res){}
   SRet(const SRet<T> &other) {this=other;}
   bool operator !() const {return retCode!=0;}
};

template<typename T>
SRet<T> MathSum(const T &arr[]){
   int size=ArraySize(arr);
   if (!size) return SRet<T>();
   SRet<T> ret(0,arr[0]);
   for (int i=1,size=ArraySize(arr);i<size;ret.res+=arr[i++]);
   return ret;
}

The method is called "whatever you like")))

I wrote it by hand, so maybe I screwed up somewhere.

 
Aleksey Nikolayev:
Cramer's theorem is in this book (Appendix, page 102).

thank you! it turns out to be very easy to prove through the (complicated) circle theorem.

 
Vladimir Simakov:

Yeah. Implementation ...

It's a lib, it's supposed to go like this:

1. At zero array returns value initialized by default constructor (for primitives it's 0)

2. At zero array, it crashes in runtime.

3. Returns a structure containing the result code and amount

The method is called "whatever you like")))

I've written it by hand, so maybe I've screwed up somewhere.

Well, it was written: "we do it as in R but faster", as in C++ it was not promised.

 
Aleksey Nikolayev:

Well, it was written "do as in R, only faster", as in C++ is not promised.

Weak excuse.

Doing as in R... I don't know, R isn't in my stack.

Except, not using templates when writing a library in C++ (if it looks like C++, smells like C++ and even has UB, that's suggestive...) - it's somehow ...

 
Aleksey Nikolayev:

https://www.mql5.com/ru/docs/standardlibrary/mathematics/stat/mathsubfunctions/statmathsum

It's in the help, but the compiler doesn't see it.
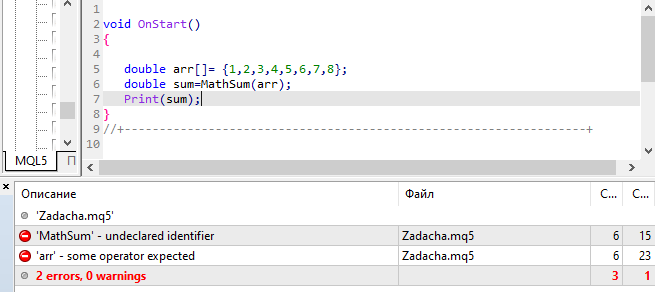
Is it just me?


I just saw that you have

#include <Math\Stat\Math.mqh>

So it must be an external library.
Once again, I don't see the point of burdening your program with additional libraries just to save a single line of code.

 
Nikolai Semko:


Once again, I don't see the point of burdening your programme with extra libraries to save a single line of code.

The program for the special case is - is. The quibbles about MathSum are insignificant

on the background of more essential problem: above noticed that this solution works only if the centre of the circumscribed circle gets inside the figure.

That is, we need another criterion of applicability. "for this one you're welcome, but for this one I can't".

Now the topic is directly related to optimizer optimization...

 
Maxim Kuznetsov:

the programme for the special case is there - it is there. The quibbles about MathSum are insignificant

on the background of more essential problem: above noticed that this solution works only if the centre of the circumscribed circle falls inside the figure.

That is, we need another criterion for applicability. "for this one you're welcome to get results, but for this one I can't".

Now the topic is directly related to optimizer optimization...

At first glance, only the equation for determining R will change.

1) In the case of the centre inside: A1+A2+...+An=2*Pi
2) In the case of the centre outside: A1-A2-...-An=0, where A1 is the angle for the longest side.

Hence, we only need to determine how to distinguish between the two cases.

PS. In general, you need to calculate the sum of angles Ai provided that the radius is equal to half of the maximum side. If it is less than 2*Pi, then the centre is outside the polygon and vice versa.

 
Maxim Kuznetsov:

the programme for the special case is there - it is there. The quibbles about MathSum are insignificant

on the background of more essential problem: above noticed that this solution works only if the centre of the circumscribed circle falls inside the figure.

That is, we need another criterion for applicability. "for this one you're welcome, but for this one I can't".

Now the subject is directly related to optimizer optimization...

Why can't I do it?
You just need time to spend, but for what purpose - is not clear.

I think Simakov already did it. True, I did not understand it.

All right, I'll try it my way. To make everything visually clear.

 

Files:
Zadacha3.mq5  9 kb
12345678
New comment