The St Petersburg phenomenon. The paradoxes of probability theory. - page 2

New comment
 
Vitalii Ananev:

:) The same scheme was used in the past by crooks, and it is likely to be used now by crooks of various stripes as well. The main thing for them is for the victim to hand over the money and they will never get it back.

And once I was at a car market in Yuzhny Port when they "took" a sucker for three cards...

It's pretty hard to tell. At one point I was sure the sucker was going to win...

After that, one day I was driving home late. There are very few people outside the underground... ...and there's some guys sitting around, and they're throwing these three cards around. I pick up and briefly tell them the story, followed by the question, "How do you do it?". Turns out it's simple. All the cards have one pinky swipe to bend a corner that the dealer didn't see... ...but in fact, he's turned the corner of another card, and the one that was turned, by a fake player, he un-turned.

  
//+------------------------------------------------------------------+
//|                                                          SPp.mq5 |
//|                        Copyright 2017, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2017, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
//--- input parameters
input int      bet=4;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart(){
   
   double me=0;
   double bank=0;
   
   while(!IsStopped()){
      
      
      double z=1.0;
      
      while(!IsStopped()){
         if(MathRand()/32768.0<0.5){
            // I win
            z=MathMin(bet,z);
            me+=z;
            bank+=(bet-z);
            break;
         }
         else{
            z*=2.0;
         }
      }
      
      Comment("Me: ",(string)me,", bank: ",(string)bank);
   
   }
   
   Comment("");

}

With a bet of 4, the game seems to be on a level playing field (if I understand the rules of the game correctly).

 
Alexey Viktorov:

And I once watched a sucker being "shopped" at a car market in South Port for three cards...

It's pretty hard to tell. At one point I was sure the sucker was going to win...

After that, one day I was driving home late. There are very few people outside the underground... ...and there's these guys sitting around throwing these three cards around. I pick up and briefly tell them the story, followed by the question, "How do you do it?". Turns out it's simple. All the cards have one pinky swipe to bend a corner that the dealer didn't see... ...but in fact, he's turned the corner of another card, and the one that was turned, by a fake player, he un-turned.

Actually, it's a lot simpler than that. Around the "gurney" always rubbing his assistants, aka the callers, they also play, sometimes win, sometimes lose. In general, they create the appearance of fair play. A random person who makes a bet in this game, even if he guesses, won't get money back. It is not important, that there are 3 cards or 3 glasses and a ball, as soon as a player opens a card or raises the glass, these helpers bend over allegedly to look closer thereby blocking the view of casual witnesses. If the player guessed, they simply challenge it saying no you didn't. If a "sucker" will be very indignant they may even kick him in the neck. The "katala" himself does not even have to try hard to confuse the player, his function is to get the bet.

 
Novaja:
The St Petersburg phenomenon
it's like the radio said to have been invented by Popov.

the usual martingale...
 
hartmann:
it's like the radio said to be invented by Popov.

a regular martingale...

unusual

 
Vitalii Ananev:

In reality, it's much simpler than that. Around the "gurney" there are always his assistants, aka the baiters, who also play, sometimes winning, sometimes losing. In general, they create the appearance of fair play. A random person who makes a bet in this game, even if he guesses, won't get his money back. It does not matter, that there are 3 cards or 3 glasses and a ball, as soon as a player opens a card or raises a glass, these helpers bend over allegedly to look closer thereby blocking the view of casual witnesses. If the player guesses, they simply challenge it by saying no, he doesn't. If a "sucker" will be very indignant they may even kick him in the neck. The "katala" himself does not even have to try hard to confuse the player, his function is to get the bet.

Have you personally seen a player make a guess but not give him the winnings? I've never seen anyone win, except their accomplices.

Those three cards or three thimbles, according to probability theory, are winnable for the organizers of the game, and then there's the sleight of hand.

 
hartmann:
it's like the radio said to have been invented by popov.

a regular martingale...

But what a chic MO, winning infinity!

 
Novaja:

But what a gorgeous MO, winning infinity!

Here, I've done the math.
for 100,000 games, the number is 8.32 roubles.
for a million games it's a number of 25.76 roubles.

The more games, the higher the number.
It's like martingale: the more you play, the more likely you are to lose.
Files:
5mro81.zip  3420 kb
 

The terms of the game are not fully described, as usual.

Is it possible to win more than your bet? If not, there is no point in playing.

Then it should be allowed to win from the pot. So it is enough to make the minimum bet, there will be a win.

Maybe the condition is that you can play 1 time, and here we have to decide on the bet, so that there would be the maximum probability of winning.

Like all "pradlocks" - from incomplete conditions.

Solution:

There's not even a question of betting. Bet 1. No more makes sense, the probability of winning doesn't depend on the size of the bet. So 1, just to start the game.

So what's the paradox? From the assumption that you have to place a bigger bet to increase your winnings? That might be it.

 
Novaja:

But what a gorgeous MO, winning infinity!

this is a non-linear function.
y=2^x.


and where does Y in a non-linear function tend if X tends to infinity? that's right, to infinity.



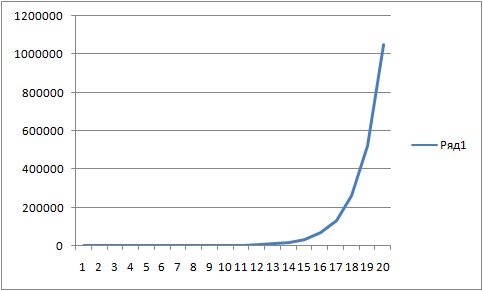
so if the number of games = infinity, then the average win = infinity.

And the problem is also set in such a way that his losses are a linear function (always 25 rubles each), and his winnings are a non-linear function.

You need to plot two functions. First the first graph will be higher than the second, then they will swap places.

Everything depends on the number of games.
123456789...25
New comment