I want to share an unexpected, simple and useful finding with programmers.
The rounding functions:
Have proven to be very slow. To speed up the rounding process by 4-5 times (according to my tests in MQL5), you can replace these functions with a simple alternative:
Since these functions are often used in large and nested loops, the performance gain can be quite significant.
Probably, the fact of calling a function is quite time-consuming (storing of different data, addresses, etc.). And in this case you can do without functions.
Script file with performance test attached.
Only I with this line
y=round(x); -> y=(int)(x+0.5);
I don't agree with this line. According to the rules of mathematics, if the fractional part is less than 0.5, rounding is done to the lower side. But if you add 0.5 to 45.27, it is rounded to the higher side.
Only I don't agree with that line.
I don't agree. According to the rules of mathematics, if the fractional part is less than 0.5, it is rounded down. But if you add 0.5 to 45.27, it is rounded to the higher side.
#define MUL(x) ((x)+(0.5)) //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { ulong t0,t1,t2,t3; int y0[],y1[],y2[]; ArrayResize(y0,10000000); ArrayResize(y1,10000000); ArrayResize(y2,10000000); double x=1.45; for(int i=0;i<10000000;i++) { if ((int)(x+0.5)!=(int)round(x)) Print("ой...",x); x+=0.27; y0[i]+=0; y1[i]+=0; y2[i]+=0; } Print("y0[]: ",y0[9999999]," / y1[]: ",y1[9999999]," / y2[]: ",y2[9999999]); x=1.45; t0=GetMicrosecondCount(); for(int i=0;i<10000000;i++) { y0[i]=(int)MathRound(x); x+=0.27; } t1=GetMicrosecondCount()-t0; Print("y0[]: ",y0[9999999]); x=1.45; t0=GetMicrosecondCount(); for(int i=0;i<10000000;i++) { y1[i]=(int)(x+0.5); x+=0.27; } t2=GetMicrosecondCount()-t0; Print("y1[]: ",y1[9999999]); x=1.45; t0=GetMicrosecondCount(); for(int i=0;i<10000000;i++) { y2[i]=(int)MUL(x); x+=0.27; } t3=GetMicrosecondCount()-t0; Print("y2[]: ",y2[9999999]); Print("Цикл округления 10 000 000 раз: (round) = ",IntegerToString(t1)," альтернатива с (int) = ",IntegerToString(t2)," альтернатива с (#define) = ",IntegerToString(t3)," микросекунд"); } //+------------------------------------------------------------------+
Only I don't agree with that line.
I don't agree. According to the rules of mathematics, if the fractional part is less than 0.5, it is rounded down. But if you add 0.5 to 45.27, it's rounded up to the higher side.
You're confused. I purposely put a check code in the example:
for(int i=0;i<10000000;i++) { if ((int)(x+0.5)!=(int)round(x)) Print("ой...",x); x+=0.27; }
If I was wrong, thePrint("oops...",x) operator would be executed;
Try it - it's OK.
I'm the only one with that line.
don't agree. According to the rules of mathematics, if the fractional part is less than 0.5, it is rounded down. But if you add 0.5 to 45.27, it's rounded to the higher side.
How about taking it and checking it out? ))) How would int(45.27 + 0.5) give 46? The same 45 will remain.
I wasn't talking about speed.
You must be confused. I purposely inserted a check code in the example:
if I was wrong, then thePrint("oops...",x) statement would be executed;
Try it - it's OK.
But it's still interesting that the speed changes if the array isnot filled with databeforehand
#define _round(x) (int)((x)+(0.5)) //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { ulong t0,t1,t2; int y0[],y1[]; ArrayResize(y0,10000000); double x=1.45; for(int i=0;i<10000000;i++) { if ((int)(x+0.5)!=(int)round(x)) Print("ой...",x); x+=0.27; y0[i]+=0; // !!!!!!!!!!!!!! } x=1.45; t0=GetMicrosecondCount(); for(int i=0;i<10000000;i++) { y0[i]=(int)(x+0.5); x+=0.27; } t1=GetMicrosecondCount()-t0; x=1.45; t0=GetMicrosecondCount(); for(int i=0;i<10000000;i++) { y0[i]=_round(x); x+=0.27; } t2=GetMicrosecondCount()-t0; Print("Цикл округления 10 000 000 раз: с (int) = ",IntegerToString(t1)," с (#define) = ",IntegerToString(t2)," микросекунд"); } //+------------------------------------------------------------------+
and filled
#define _round(x) (int)((x)+(0.5)) //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { ulong t0,t1,t2; int y0[],y1[]; ArrayResize(y0,10000000); double x=1.45; for(int i=1;i<10000000;i++) { if ((int)(x+0.5)!=(int)round(x)) Print("ой...",x); x+=0.27; y0[i]+=1; // !!!!!!!!!!!!!! } x=1.45; t0=GetMicrosecondCount(); for(int i=0;i<10000000;i++) { y0[i]=(int)(x+0.5); x+=0.27; } t1=GetMicrosecondCount()-t0; x=1.45; t0=GetMicrosecondCount(); for(int i=0;i<10000000;i++) { y0[i]=_round(x); x+=0.27; } t2=GetMicrosecondCount()-t0; Print("Цикл округления 10 000 000 раз: с (int) = ",IntegerToString(t1)," с (#define) = ",IntegerToString(t2)," микросекунд"); } //+------------------------------------------------------------------+
How about checking it out? ))) How would int(45.27 + 0.5) give 46? The same 45 will remain.
I agree, I lost my train of thought. I take it back...
But it is still interesting that the speed changes if the arrayis not filled with databeforehand
and fill it
y0[i]+=0; // !!!!!!!!!!!!!!I find "#define" more convenient
#define _floor(x) (int)((x)) #define _ceil(x) (int)((x)+(1)) #define _round(x) (int)((x)+(0.5))
Why don't you cast to the long? Although you can overflow it too, it's a lot easier to overflow an Int.
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use


I want to share an unexpected, simple and useful finding with programmers.
The rounding functions:
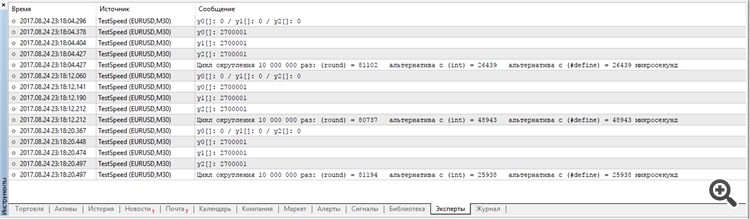
Have proven to be very slow. To speed up the rounding process by 4-5 times (according to my tests in MQL5), you can replace these functions with a simple alternative:
Since these functions are often used in large and nested loops, the performance gain can be quite significant.
Probably, the fact of calling a function is quite time-consuming (storing of different data, addresses, etc.). And in this case you can do without functions.
File of script with performance test attached.