Well, what if we say (just by eye) that it is a sine, with a constantly increasing period (depending on X), i.e. a formula like this:
General (where we're coming from):
Y=sin( K*X+T)
Now we say that the parameter K also depends on X. All the time it is increasing or decreasing. The question arises: is it linear? I would assume linearly to begin with. Then it is A*X+B (line formula). Substituted in the original formula, we get
Y=sin((A*X+B)*X+T)=sin(A*X^2+BX+T).
Here we have a starting point. Polynomial under the sine sign. Run regression.... etc. - I hope I explained it clearly. I'd like to make a program for you in Matlab, but I have no time, you'll have to do it yourself.
Let me explain a little bit about what this is for. I have an idea for TC based on a predicate. From those known to me and more or less available are Fourier and regression. Applied to Fourier. The underlying assumption is that the parameters are stationary. On a normal sine wave, everything looks fine
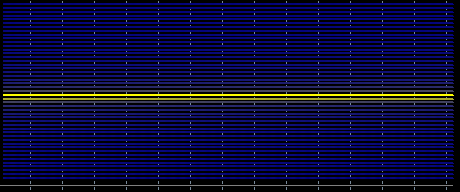
But if we take a smoothly varying period, the spectrum is smeared out
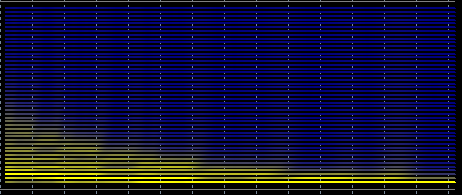
and therefore you can't get an adequate prediction.
I could not get anything good on regression either.
Therefore we need to look for other methods that are more "adaptive" or something like that. That is what I wanted to know about.
You have a smooth curve. Therefore, the methods of differential analysis are applicable to it. Even without knowing that it is a sine with a variable period, you can use a Taylor series expansion with retention of the first few terms. Further, you can use it to predict the value of a future reference by substituting a few previous terms into the formula. I can assure you the result will amaze you with its prediction accuracy. The error will be zero.
And it won't work for price series, because in decomposition in RF you will get PDF and you will not have to predict one count forward, but for the number of counts that fits into the PDF scale and that's where the prediction error will jump.
Nature cannot be fooled.
And all this will not work for price series, because when you decompose into RF you will get an FZ and you will have to predict not one count forward but the number of counts that fit on the scale of the FZ and it is at this distance that the prediction error will increase dramatically.
Nature cannot be fooled.
That's understandable. But it is possible to assume that the parameters do not change over a period of time. With the top picture I wanted to show that the result can be bad not only from non-stationarity, but also from an unsuitable method.
That is clear. But it is possible to assume that the parameters do not change for some time. With the top picture I wanted to show that the result can be bad not only from non-stationarity, but also from an unsuitable method.
The hypothesis of a stationary market has never been confirmed. Therefore, it cannot be assumed that the parameters will remain constant over any time horizon, however small.
Let me explain a little bit about what this is for. I have an idea for TC based on a predicate. From those known to me and more or less available are Fourier and regression. Applied to Fourier. The underlying assumption is that the parameters are stationary. On a normal sine wave, everything looks fine
But if we take a smoothly varying period, the spectrum is smeared out
and therefore you can't get an adequate prediction.
I could not get anything good on regression either.
Therefore we need to look for other methods that are more "adaptive" or something like that. That is what I wanted to know about.
what can a wavelet do?
ZS: I made a .dll with code from BaseGroup.ru for MT5, but I haven't found any practical use yet http://imglink.ru/pictures/18-01-12/4e3891b89673e8f79e194b5a86a25d41.jpg
The hypothesis of a stationary market has never been confirmed. Therefore, it cannot be assumed that the parameters remain constant over any time horizon, however small.
I am not talking about complete stationarity, but perhaps there are sections where the parameters are more or less stable. Otherwise, how else to explain that the strategies can work for some time. There is an approach where one makes several strategies and switches between them, the question is how to determine the moment of switching.
www.https://www.mql5.com/ru/forum/127297 There is indirect evidence of temporal predictability here.
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
There is a picture like this:
What methodology can extrapolate a series like this?
Could someone put this into a neural network for an experiment?