Pure maths, physics, logic (braingames.ru): non-trade-related brain games - page 125
You are missing trading opportunities:
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
Registration
Log in
You agree to website policy and terms of use
If you do not have an account, please register
It seems to fit all the options in 2 weighing
this drawing is something alien...
Weird, I thought it was clearer, I think the picture is more illustrative than words. OK, a few comments:
For the first weighing we put two balls on each cup of the scales, so that we have in each cup 1 ball of the chosen colour and one ball of some other colour different from the colours of the balls in the opposite basket. (In the picture it is a red ball with a green one and a red ball with a blue one). The results of 1 weighing may be different: option 1.1) the scales are balanced and option 2) the scales are unbalanced, one of the cups outweighs 2.1). That is, we have two branches of the solution.
If the first variant, we divide the balls into two homogeneous groups (group ' and group '), and then 1.2) we simply weigh both groups (3 balls per cup of the balance) and determine which one is heavy. That's it, the heavy balls are found.
The second option can happen for two (generalized) cases. When both coloured balls from the first weighing in each cup are either heavy or light. By (2.2) after marking the balls into groups (group ' and group ') we determine with a single weighing with a heavy ball, which of the groups belongs to the heavy group and which to the light one.
This is a picture from the internet....
OK, a few comments:
Now the pattern is clear.
The second option can happen for two (generalised) cases. When both the coloured balls from the first weighing in each cup are either heavy or light.
Weird, I thought it was clearer, I think the picture is more illustrative than words. OK, a few comments:
For the first weighing we put two balls on each cup of the scales, so that we have in each cup 1 ball of the chosen colour and one ball of some other colour different from the colours of the balls in the opposite basket. (In the picture it is a red ball with a green one and a red ball with a blue one). The results of 1 weighing may be different: option 1.1) the scales are balanced and option 2) the scales are unbalanced, one of the cups outweighs 2.1). That is, we have two branches of the solution.
If the first variant, we divide the balls into two homogeneous groups (group ' and group '), and then 1.2) we simply weigh both groups (3 balls per cup of the balance) and determine which one is heavy. That's it, the heavy balls are found.
The second option can happen for two (generalised) cases. When both coloured balls from the first weighing in each cup are either heavy or light. By (2.2) we determine with a single weighing (group ' and group '), which one is the heavy one and which one is the light one.
Keep your doubts to yourself. CensoredNo offence meant...
Option 1.1 I suggested in private. the beginning is wrong.
Thanks for the congratulations, guys, but the truth comes first!
In short: two or three?
If two, give me a diagram, as I know for three myself.
Right thanks, then the second branch of the solution diverges into three options (option c is added)
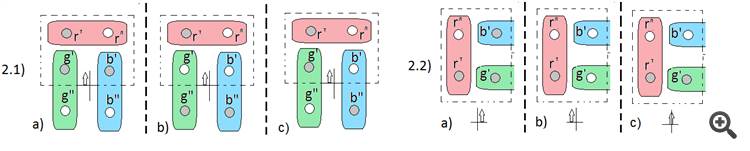
And the second weighing will be organised from the same balls as the first, but in a different arrangement. As a result, after the second weighing we will have one of the three answers, by which we can reconstruct the position of the balls in the first weighing, and knowing the heavy ball from the first weighing (the green heavy one) we can determine the weight of the others.Andrei, what's your solution for the three balls (just the initial lay-out for each weighing is enough)?
There is an opinion that there are several solutions.
Andrei, what's your solution for three balls (just the initial lay-out for each weighing is enough)?
I don't have an option :) the solution above seems to be correct.
______________
And happy birthday :) More interesting puzzle problems for you and to solve them all.
I don't have an option :) the solution above seems to be the right one.
______________
And happy birthday :) I wish you many interesting puzzle problems and that you solve them all.
Thanks, Andrew.
I'm afraid I'll have to post the ones I haven't solved more often. But solve them urgently (I don't like reading other people's solutions if I haven't solved them myself)!
P.S. Did you solve the 53 problem?