Otavio Barreto: can somebody help to make it show the inverse band?
- Your version is a repainting version — useless for trading.
- Until you can define concretely what you mean by "inverse band" no one can help you. The COG is x[1] + x[2]
2 + x[3]
3…
- Help you with what? You haven't stated a problem, you stated a want. Show us your attempt (using the CODE button)
and state the nature of your problem.
No free helpOr pay someone. Top of every page is the link Freelance.
Hiring to write script - General - MQL5 programming forum
Fitting a parabola - MQL4 programming forum Not John Ehlers' Center of Gravity oscillator.
You are missing trading opportunities:
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
Registration
Log in
You agree to website policy and terms of use
If you do not have an account, please register
this will give me this result
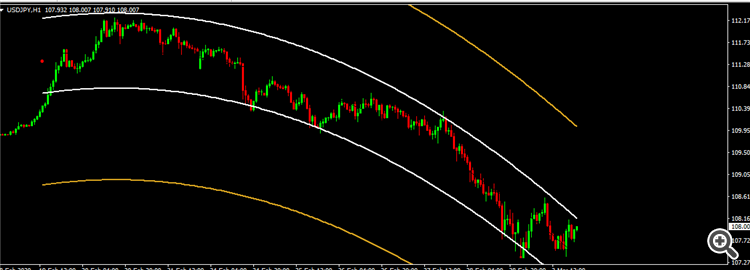
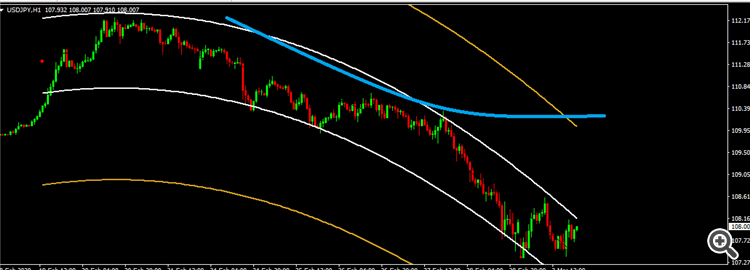
But I would like some help to make it looks like this:
The blue line is the inverse of the center of gravity, can somebody help to make it show the inverse band?