int n = 9; int a_array[][]; a_array[0][0] = 1; for(int i=1;i<=n;i++) { for(int k=0;k<=(2*i);k++) { a_array[i][k] = ((k-2)>=0)?a_array[i-1][k-2]:0 + ((k-1)>=0)?a_array[i-1][k-1]:0 + (k<=(2*i))?a_array[i-1][k]:0; }; };Perhaps I am getting closer. Am I?
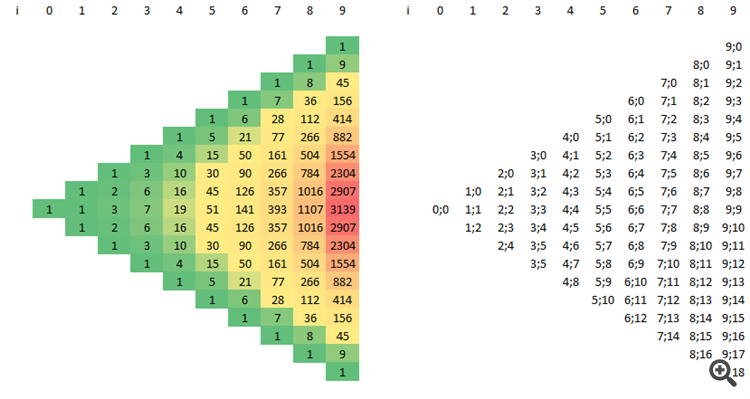
I saw another trader trading bimodal - multimodal distributions.But how do you trade the bimodal - multimodal distributions ?Do you evaluate your trading results on multimodal trinomial distribution criteria? Do you trade the multimodal trinomial distribution of price? etc..
When I google ''multimodal trinomial distribution criteria for trading'' I can only find few papers based on option pricing.
I saw another trader trading bimodal - multimodal distributions.But how do you trade the bimodal - multimodal distributions ?Do you evaluate your trading results on multimodal trinomial distribution criteria? Do you trade the multimodal trinomial distribution of price? etc..
When I google ''multimodal trinomial distribution criteria for trading'' I can only find few papers based on option pricing.
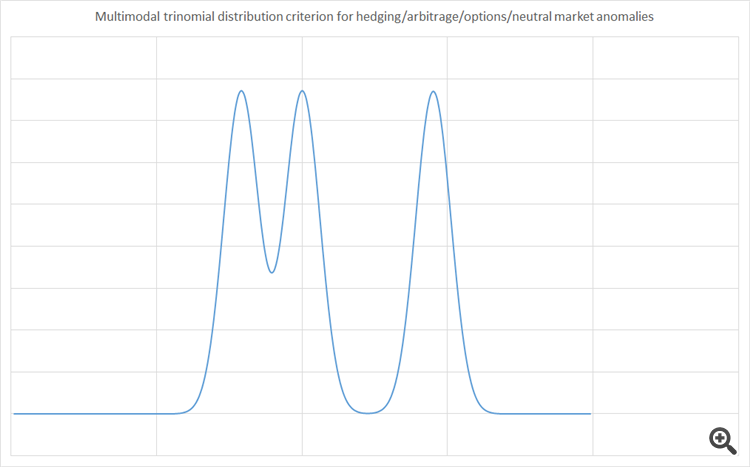
Take a close look at the following book and tell me if there is a support and resistance based on the volumes. Where will the price land?
If you want to do this in MQL the problem is the dynamic 2-dimensional array. As far as I know you can only resize one dimension but not two. Let's assume you know the maximum value of n, say MAX_N, that would make things easier.
What you want is the Trinomial Triangle as shown in #4, especially the values of the center row (1,1,3,7,19,...) and the sum thereof. From all what I've read in the article you have to compute the values recursively.
#define MAX_N 10 int Triangle[MAX_N+1][MAX_N+1]; void TriangleInit() { Triangle[0][0] = 1; for(int n=1;n<=MAX_N;n++) { for(int k=0;k<=n;k++) { Triangle[n][k] = (k-1>=0 ? Triangle[n-1][k-1] : Triangle[n-1][1]) + (n-1>=k ? Triangle[n-1][k] : 0) + (n-1>=k+1 ? Triangle[n-1][k+1] : 0); } } } int Trinomial(int n,int k) { if(k<0) k=-k; return (n>=0 && k<=n ? Triangle[n][k] : 0); }
The rows of the triangle are counted from 0 upwards that is n>=0, and the middle column is denoted by k=0. That means Trinomial(4,0) is expected to return 19 (row 4, middle column.)
The sum of all values above a center value at row n is built by summing up Trinomial(i,0) for i<n.
- en.wikipedia.org
Take a close look at the following book and tell me if there is a support and resistance based on the volumes. Where will the price land?
An order book means nothing. Virtual SL/TP, Iceberg orders, even fake
orders, volume that is not executed could mean anything. Why throw heavy computations against an order book?

- en.wikipedia.org
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
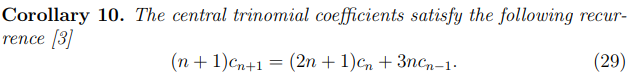

Let's take the following polynomial (which is closely related to the binomial expansion, and it is in fact a particular case of trinomial expansion):
It's expansion gives a series of coefficients, depending solely on n.
and so on...
The sum of the coefficients is simply n3.
The function, I believe, should look like this: