Diskussion zum Artikel "Leistungsfähige adaptive Indikatoren - Theorie und Umsetzung in MQL5"
Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich
Neuer Artikel Leistungsfähige adaptive Indikatoren - Theorie und Umsetzung in MQL5 :
Dieser Beitrag behandelt leistungsfähige adaptive Indikatoren und ihre Umsetzung in MQL5. Die Indikatoren Adaptive Cyber Cycle, Adaptive Center of Gravity und Adaptive RVI wurden alle ursprünglich von John F. Ehlers in „Kybernetische Analyse für Wertpapiere und Terminkontrakte“ (Cybernetic Analysis for Stocks and Futures) vorgestellt.
Der Phasenvektor
Bei dem auch als Phasor bezeichneten Phasenvektor handelt es sich um einen Vektor, der die Amplitude und die Phase eines periodischen Ablaufs (Zyklus) angibt. Gemäß der Eulerschen Formel kann eine komplexe Zahl (bestehend aus einem Real- und einem Imaginärteil) in einer Form abgebildet werden, in der ein Winkel als Argument in der Phase erscheint. Das ermöglicht die anschauliche Darstellung periodischer Abläufe (Zyklen). Die Abbildung unten beinhaltet eine Animation, die die Rotation des Phasenvektors der Sinuskurve abbildet.
Mag sein, dass sich beim ersten Anblick dieser Animation die Frage aufdrängt, in welcher Beziehung der Phasenvektor zum Ablauf steht. Zum Verständnis ist es besser, den periodischen Ablauf als den rechts abgebildeten rotierenden Phasenvektor zu betrachten und nicht in Form der üblichen Sinuskurve links.
Ich stelle mir das folgendermaßen vor: die volle Umdrehung des Phasenvektors um 360° (oder einen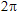
-Radian)
ist über den gesamten Zyklus identisch. Der jeweils aktuelle Winkel des
Phasenvektors zeigt an, in welchem Teil des Zyklus (welcher Phase) wir
uns befinden. Die y-Achse bildet die Amplitude des periodischen Ablaufs
ab.
Der Phasenvektor kann in zwei Bestandteile aufgegliedert werden: InPhase (Kosinus) und Quadratur (Sinus). Eine ausführliche Darstellung der Ermittlung dieser Bestandteile liefert Kapitel 6 „Die Hilbert-Transformationen“ in „Raketenwissenschaft für Börsenhändler“ (Rocket Science for Traders). Dieses Kapitel lege ich allen ans Herz, die sich eingehender damit befassen möchten.
Momentan kommt es für uns lediglich darauf an, dass wir zur Berechnung der adaptiven Indikatoren ein Signal (in Wellenform) in ein aus zwei Bestandteilen zusammengesetztes komplexes Signal umwandeln müssen. Wie erreichen wir das? Habe ich die Hilbert-Transformation bereits erwähnt? Ja tatsächlich. Genau das vermag die Hilbert-Transformation zu tun.
Autor: investeo