Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich
Nun zu seiner Nützlichkeit (Relevanz). Konstruktionsbedingt handelt es sich immer um eine alternierende Reihe. Was schlagen Sie vor, um in den Mustern zu suchen, das Verhältnis der Kagi-Zickzack-Seiten?
Auch die Muster selbst, denn.
Die RT ist eine Ableitung der Konstruktion kaga, die RT selbst ist nur eine Zahl N - 1 auf jedem N-langen kaga-Segment, habe ich das richtig verstanden?
Wenn ja, dann sollte auch der PT abwechselnd sein.
Wenn nein, erklären Sie dann, wie die korrekte Konstruktion einer Cagi es ermöglicht, mehrere PTs desselben Vorzeichens in einem Cagi-Segment zu erhalten?
Um genau zu sein, behandelt Pastukhov die Kagi-Muster
und Tabelle 3.1 spricht über Kagi-Muster
Ich schlage vor, die primären Daten - Kagi-Muster - zu verwenden und auf der Grundlage ihrer Eigenschaften PTs zu erstellen.
Ich denke also, dass es wichtig ist:
Die RT ist eine Ableitung der Konstruktionscagi, die RT selbst ist nur eine Zahl N - 1 auf jedem N-langen Cagi-Segment, verstehe ich das richtig?
Ja, das ist richtig.
Wenn ja, dann sollte die RT auch vorzeichenvariabel sein. Wenn nicht, erklären Sie, wie es möglich ist, mehrere RTs desselben Vorzeichens auf demselben Kagi-Segment zu erhalten, wenn die Kagi-Konstruktion korrekt ist?
Nein, diese Aussage ist nicht korrekt. Um sich davon zu überzeugen, genügt es, die notwendigen Konstruktionen einmal durchzuführen:
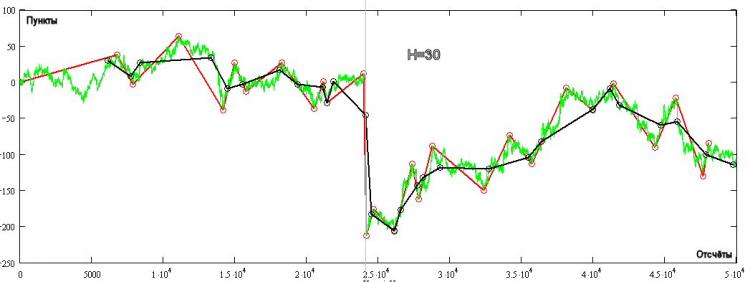
In der Abbildung zeigt das Grüne den Tick Quotire, das Rote ist die Kagi-Konstruktion (immer vorzeichenvariabel) für H=30 Pips, und das Schwarze ist der PT. Es gibt eine ganze Reihe von Bereichen, in denen PT nicht vorzeichenvariabel ist! Wie dies geschieht, ist aus dem Diagramm ersichtlich - der nächste TP-Wert ergibt sich, wenn sich der Kurs um mehr oder gleich H von der Spitze entfernt. Der TP ändert sich nicht, je nachdem, welche Strategie Sie verfolgen (H+ oder H-), er hängt nur von der Richtung der bei jedem TP-Wert eröffneten Position ab.
Ich schlage vor, Primärdaten - Cagi-Muster - zu verwenden und auf der Grundlage ihrer Eigenschaften PTs zu erstellen.
Deshalb halte ich sie für wichtig:
Ein Gegenvorschlag besteht darin, eine Einigung in wichtigen Fragen zu erzielen.
Versuchen Sie z. B., einen Konsens in der Frage möglicher kognitiver PTs zu erzielen, und dann, dass es für die weitere Diskussion ausreicht, nur PTs zu verwenden, ohne sich auf das ursprüngliche Kagi-Muster zu berufen. Und schließlich, dass es notwendig und ausreichend ist, die RT-Reihe der ersten Differenz für die Analyse zu verwenden (auch wenn Pastuchow dies nicht tut), was die Musteranalyse deutlich vereinfacht!
Wenn Sie, Michael, eine andere Vorstellung von der Lösung dieses Problems haben, würde ich mich freuen, die Ergebnisse Ihrer Forschung zu lesen.
Ein Gegenvorschlag ist, sich auf die wichtigsten Punkte zu einigen.
Um zum Beispiel einen Konsens über ein mögliches Kognat PT zu testen, müssen wir für die weitere Diskussion nur PT verwenden, ohne auf das ursprüngliche Kagi-Gebäude zurückzugreifen. Und schließlich, dass es notwendig und ausreichend ist, die RT-Reihe der ersten Differenz für die Analyse zu verwenden (auch wenn Pastuchow dies nicht tut), was die Musteranalyse deutlich vereinfacht!
Wenn Sie, Michael, eine andere Vorstellung von der Lösung dieses Problems haben, würde ich mich freuen, die Ergebnisse Ihrer Forschung zu lesen
Es zeigt sich ein Unterschied in der Definition von DH:
Lassen Sie uns Ihre Definition verstehen.
Wie unterscheidet sie sich von einer Renko-Serie?
Wenn nicht, dann stehen wir vor der Wahl zwischen Kagi und Renko als Musterbildungsmethode für die Vorhersage.
Auf den Seiten 82-85 bewertet Pastuchow die statistische Stabilität dieser beiden Reihen und kommt zu dem Schluss
Es ist nur logisch, die stabileren als Prädiktoren zu nehmen.
Was sind Ihre Argumente für die Wahl der Renko-Konstruktion als Prädiktor?
Ich spreche von Kagi-Konstruktionen.
Der Unterschied zwischen Renko und Kagi, so die These, besteht darin, dass bei Renko-Gebäuden der Abstand zwischen den Scheitelpunkten des Renko-Zickzack immer ein Vielfaches von H ist und immer größer oder gleich H ist. Bei Kagi kann dieser Abstand beliebig sein und ist immer größer oder gleich H.
Michael, schauen Sie sich das Bild oben an, für Kagi Konstruktionen (die in rot), kann die Segmentlänge 3.14H sein, Auf dem gleichen Abschnitt, Renko kann nur 3H sein. Das ist der Unterschied!
Und ich stimme Ihnen voll und ganz zu, dass Renko keine Konkurrenz ist und es keinen Sinn hat, diese Aufschlüsselung in Betracht zu ziehen.
Ich spreche von Kagi-Konstruktionen.
Der Unterschied zwischen Renko und Kagi, so die These, besteht darin, dass bei Renko-Gebäuden der Abstand zwischen den Scheitelpunkten des Renko-Zickzack immer ein Vielfaches von H ist und immer größer oder gleich H ist. Bei Kagi kann dieser Abstand beliebig sein und ist immer größer oder gleich H.
Michael, schauen Sie sich das Bild oben an, für Kagi Konstruktionen (die in rot), kann die Segmentlänge 3.14H sein, Auf dem gleichen Abschnitt, Renko kann nur 3H sein. Das ist der Unterschied!
Und ich stimme Ihnen voll und ganz zu, dass es keine Konkurrenz für Renko gibt und es keinen Sinn hat, diese Aufteilung in Betracht zu ziehen.
Lassen Sie uns noch einmal langsam und einfach vorgehen:
Ohne zu fragen: "Wie heißt die resultierende stückweise monotone PT-Funktion?"
Wir sollten uns die Fragen stellen:
Ich habe eine grobe Antwort auf die erste Frage: Es handelt sich um eine Art MA, d.h. um einen Versuch, eine Preiszeitreihe zu mitteln.
Ich hoffe, dass Sie dem zustimmen werden.
Die zweite Frage lautet dann: Warum ist er als Prädiktor besser als ein N-quantisierter MA?
ist eine Art MA, d. h. ein Versuch, die Preiszeitreihen zu mitteln.
Ich hoffe, Sie stimmen dem zu.
Ja, ich weiß.
Die zweite Frage lautet dann: Wie überlegen ist er als Prädiktor für denselben N-quantisierten MA?
Mashka wird unabhängig von den versteckten Mustern des geglätteten BP eine konstante FP haben. Wenn wir etwas Ähnliches wie FP für RT einführen, ist ein interessantes Phänomen zu beobachten: Je mehr sich BP von einem Wiener-Prozess unterscheidet, desto weniger hat FP RT. Das heißt, die maximale PT-Verzögerung wird bei einem integrierten Zufallsprozess beobachtet, und quantitativ weist der PT nicht die Eigenschaft der Vorzeichenvariabilität auf. Sobald der Markt jedoch arbitragefähig wird, weist der PT Vorzeichen-Varianz-Eigenschaften auf und sein "Lag" wird reduziert.
Mit anderen Worten, der "Glättungseffekt" für den PT wird nur bei einem solchen H beobachtet, bei dem der Markt arbitragefrei ist (der durchschnittliche Kagi-Segmentwert tendiert zu 2H), und dies kann als Signal dienen, um durch den Parameter H zu anderen Handelshorizonten überzugehen.
Erklären Sie mir das bitte, ich arbeite seit ich weiß nicht wie lange im Finanzwesen und der Begriff Transaktion wurde immer verwendet.
Und jetzt schaue ich auf wikipedia, angeblich ist es im Bankwesen eine Transaktion. Es ist sehr seltsam, eine Fettabsaugung...
Wer kann sich dazu äußern?
Korrigieren Sie es also selbst in dieser WikiPedia.
Ich denke, die Transaktion ist auch korrekter.
Mit anderen Worten, der "Glättungseffekt" für PT wird nur bei einem solchen H beobachtet, bei dem der Markt arbitragefrei ist (die durchschnittlichen Kagi-Segmente tendieren zu 2H), und dies kann als Signal dienen, mit dem Parameter H zu anderen Handelshorizonten zu wechseln.
Serge, ich werde vorerst auf Vergleiche mit anderen Konstruktionen und Ansätzen verzichten (ich muss das Thema zu Ende bringen),
Vielleicht kommen wir später darauf zurück. Doch nun zum Thema Kagi:
Da die H-Volatilität von der Wahl von H abhängt, sind für eine vollständige Kagi-Analyse zwei weitere Metriken erforderlich.
1) Ein Diagramm der H-Volatilität als Funktion von H. (Horizontale H, vertikale H-Volatilität)
2) Ein Diagramm der Volatilität der H-Volatilität selbst. Einfach ausgedrückt: ein Diagramm der H-Volatilität als Funktion von
Zeit (bei festem H). Sie können nicht ohne sie auskommen. Wenn die Krümmung zu stark ist, gibt es an diesen Stellen nichts zu fangen.
Warum versuchen Sie nicht, ein dreidimensionales Diagramm zu erstellen (x=t, y=H, z=HVol)?
2) Ein Volatilitätsdiagramm der H-Volatilität selbst. Einfacher ausgedrückt, ein Diagramm der H-Volatilität als Funktion von
Zeit (für ein festes H). Sie können nicht darauf verzichten. Wenn die Krümmung zu stark ist, gibt es an diesen Stellen nichts zu fangen.
Ich werde versuchen, mein Verständnis der Situation zu skizzieren.
Um die Handelsaussichten eines Instruments beurteilen zu können, müssen Sie eine quantitative Einschätzung der Vorhersagbarkeit haben
Mit anderen Worten - wir arbeiten mit
für ein bestimmtes Instrument, wenn (und solange) es mindestens ein H-Volatilitätszeichen gibt, für das die H-Volatilität
ist zum Zeitpunkt der Transaktion (tT) vorhersehbar, was wiederum von der Wahl von Н abhängt.
D.h. eine zweidimensionale Tabelle ist ohnehin erforderlich (die Werte in den Zellen sind die dritte Dimension). Die Ausbreitung spielt im Moment keine Rolle.
Wo wir gerade beim Thema Kagi sind:
Da die H-Volatilität von der Wahl von H abhängt, sind für eine vollständige Kagi-Analyse zwei weitere Metriken erforderlich.
1) Ein Diagramm der H-Volatilität als Funktion von H. (Horizontale H, vertikale H-Volatilität)
Hier ist sie:
Nachstehend habe ich eine Datei im Textformat mit Zeilen von Transaktionen beigefügt.
Das Format der Datei ist wie folgt: