Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich
Nein, das ist es nicht. Nach dieser Formel scheint es, dass der GVH korreliert ist. Die ganze Zeit über liegt r bei minus 0,5.
Hier ist der Testcode.
Ich habe es überprüft.
Sergei, lassen Sie uns einen Schritt nach dem anderen machen.
1. Wir arbeiten mit einem BP, der einem Angebot ähnelt. Eine solche Reihe erhält man durch Integration von CB mit Null MO. Beispiel einer Zentralbank mit null MO:
dX=rnorm(n+1,0,10), wobei n+1 die Anzahl der CB-Mitglieder ist, die eine Gaußsche Verteilung haben, 0 ist MO gleich Null in meinem Fall und 10 in Ihrem Beispiel, 10 ist die Breite dieser Verteilung in meinem Fall und 100 in Ihrem. Um den BP ähnlich wie den Preis zu konstruieren, müssen wir die ursprüngliche Reihe integrieren (ihre kommutative Summe finden):
So sehen die Verteilungen der Inkremente des integrierten CB aus (Abb. links) und die Inkremente selbst vor dem Hintergrund des BP (rote und blaue Linien in der rechten Abb.):
Sergej, wir untersuchen die Eigenschaften von BP (der blauen), während Sie in Ihrem Beitrag die allererste Differenz (dX in meiner Notation und X in Ihrer) in die Formel zur Berechnung des Korrelationskoeffizienten der ersten Differenz in der Reihe eingesetzt haben. Natürlich erhält man R=0,5, und es sollte keine weitere geben (das ist elementar bewiesen). Wenn Sie nun mit der von mir vorgeschlagenen Formel r für integrierte CB mit null MO (die blaue in der rechten Abbildung) berechnen, erhalten Sie die erwartete Null:
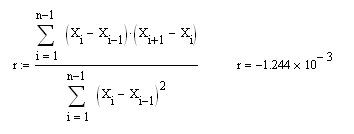
Und natürlich ist dies dasselbe wie r für eine Reihe von dX-Inkrementen (allerdings mit einer anderen Formel):
Ich hoffe, wir haben jetzt einen Konsens in diesem Punkt?
P.S. Sie können es auch so machen:
Also gut, lassen Sie uns das klarstellen.
Ich habe getan, was Sie gesagt haben, ich habe das CB mit MOJ=0 wieder integriert. Hier ist der gesamte Code.
Auf den ersten Blick sieht es gut aus. Doch es gibt einen Haken. Geben wir ein korreliertes Array in die Eingabe der Formel ein. Wie Trend + Rauschen. y=a*x+b+rnorm(). Dies kann einfach durch die Einstellung von 0,5 anstelle von MOJ=0 geschehen.
Aus der Abbildung ist ersichtlich, dass die Kurve (blau) eindeutig korreliert ist. Nach der Aufteilung in zwei Felder A und B berechnen wir den Korrelationskoeffizienten, der 0,993 beträgt. Nach Ihrer Formel sind es 0,225.
Das Problem ist, dass der Korrelationskoeffizient (CC) per Definition zwischen den beiden Feldern gezählt wird. Sie benutzen denselben. Sie können dies tun, indem Sie ein Array mit sich selbst vergleichen. Es wird ACF genannt, d.h. es werden zwei Arrays A gebildet - das erste und das zweite B, das relativ zu A zeitlich verschoben ist, und es wird ein Graph erstellt - die Abhängigkeit des Korrelationskoeffizienten von der Verschiebung. Wenn es keine Verschiebung gibt, ist der ACF natürlich = 1. Hier ist die ACF-Darstellung der letzten blauen Kurve.
Dies ist der Näherungswert. Ich bleibe also bei meiner Meinung, dass Sie nach dieser Formel rechnen, aber es ist nicht AC. Die Zahlen gehen nicht auf.
Aber wir haben uns verrannt. Wir müssen zunächst den Hurst-Wert korrekt berechnen und dann sehen, wie er sich vom QC-Wert unterscheidet.
Hier ist eine interessante Arbeit, die verschiedene Zeitreihen analysiert
unter Verwendung des Hearst-Index.
Die Abbildung zeigt, dass die Kurve (blau) deutlich korreliert ist. Die Aufteilung in zwei Felder A und B ergibt einen Korrelationskoeffizienten von 0,993. Ihre Formel ergibt 0,225.
Hier verstehe ich es nicht ganz.
In welche Bereiche haben Sie den Trend BP unterteilt? In ein gerades Y=a*X+b und eine Zufallskomponente mit Null MO, und dazwischen suchen Sie den Korrelationskoeffizienten?
Hier ist eine interessante Arbeit, die verschiedene Zeitreihen analysiert
unter Verwendung des Hearst-Indexes.
Ich habe hier nicht alles richtig verstanden.
Jetzt verstehe ich es.
Gesucht wird der Korrelationskoeffizient zwischen dem ursprünglichen Blutdruck (nicht seinen Inkrementen) und demselben Blutdruck, der um 500 Zähler nach rechts verschoben ist. Das heißt, Sie suchen nach dem Korrelationskoeffizienten zwischen zwei stets positiven Blutdruckwerten! Natürlich wird sie immer positiv und sehr groß (etwa 1) sein.
Sergej, ich verstehe dich nicht! Was zählen Sie, den Korrelationskoeffizienten zwischen dem ursprünglichen Blutdruck und dem gleichen, aber verschobenen Wert? Wozu zum Teufel brauchen wir das? Wir interessieren uns für den Korrelationskoeffizienten zwischen benachbarten Stichproben in der Reihe der ersten Differenz des ursprünglichen BP. Dieser Koeffizient zeigt die Abhängigkeit des erwarteten Zuwachses von den vorangegangenen Zuwächsen. Dieser Koeffizient ist identisch mit dem um 1/2 verschobenen Hurst-Koeffizienten.
>> Danke. >> Wir werden sehen.
Da scheint etwas Wahresdran zu sein.
Ich habe versucht, sie zu implementieren, aber ich kam sehr nahe an 1 für die Preise.
______________
Lesen Sie den Artikel noch einmal - ich glaube, ich stehe auf der falschen Seite der Medaille.
Bei Währungspaaren sollte der Hearst-Index für das Derivat berechnet werden, ich habe ihn für den Wechselkurs berechnet.
Lesen Sie den Artikel noch einmal - Sie sind sozusagen auf eine Harke getreten.
Ja:-)
Ich greife mir selbst vor.
So sieht die Reihe der integrierten SV- und EURGBP-Rate aus (Abb. links), und so sehen die Amplituden ihrer Inkremente auf verschiedenen TFs in doppelt logarithmischer Skala aus (Abb. rechts), wobei auf der Abszissenachse der Logarithmus der TF aufgetragen ist:
Hers, behauptet, dass der Tangens des Steigungswinkels dieser Linien gleich 1/2 für eine integrierte Zufallsvariable ist (es macht keinen Sinn, auf einem solchen Quotienten zu handeln), kleiner als 1/2 für einen Pullback-Markt und größer als 1/2 für einen Trendmarkt. Mal sehen, was dieser Winkel für NE bedeutet. Hier können wir, wie in dem Artikel empfohlen, eine ISC-Linie zeichnen und ihre Steigung ermitteln, aber ich werde diesen Wert lokal ermitteln - indem ich eine Linie durch alle zwei Punkte zeichne. Das Ergebnis ist der PC für jede TF:
Die Kreise zeigen hier den PC für die CB (rot) und blau für den EURGBP-Quotienten auf der Abszissenachse für die TF in min. Die Kreuze zeigen den Korrelationskoeffizienten zwischen benachbarten Messwerten für die erste Differenz der ursprünglichen Reihe mit einem Offset von 1/2. Der Korrelationskoeffizient wurde nach der in der ersten Meldung auf dieser Seite angegebenen Formel berechnet. Es zeigt sich, dass die Übereinstimmung zwischen diesen beiden Methoden zur Schätzung der Vorhersagbarkeit von BP zufriedenstellend ist, während die Formeln in meinem Fall viel kleiner sind (nur eine). Genau das musste ja auch gezeigt werden.
Außerdem ergab die Zufallsreihe PX=1/2 und r=0 (in der Abbildung ist eine Verzerrung zu sehen), wie aus der Definition hervorgeht. Beim Quotienten ist ein rollierender Trend (Antipersistenz) deutlich erkennbar, je größer, desto kleiner die TF.
Hier zeigen wir PCB für CB (rot) und in blau für EURGBP kotier auf der Abszissenachse ist die TF in min aufgetragen.
Die Zufallsreihe ergab PX=1/2 und r=0 (in der Abbildung ist eine Verzerrung zu sehen), wie aus der Definition hervorgeht. Beim Kotier ist eindeutig ein rollierender Trend (Antipersistenz) zu erkennen, je größer, desto kleiner die TF.
Das ist wahrscheinlich der Grund, warum die Pips das Euro-Pfund so sehr lieben
Das ist wohl der Grund, warum die Pipsmen das Euro-Pfund so sehr lieben.
Das ist offensichtlich!
Das ist offensichtlich!
Aus reiner Neugierde - ich würde gerne extrem ausdauernde Paare finden,
oder zumindest die Bedingungen, unter denen Persistenz auftritt):