MQL5における修正グリッドヘッジEA（第3部）：シンプルヘッジ戦略の最適化(I)

はじめに

連載「シンプルヘッジ戦略の最適化」の第3部へようこそ。このセグメントでは、まずこれまでの歩みを簡単に振り返ります。これまでのところ、シンプルヘッジEAとシンプルグリッドEAという2つの主要なコンポーネントを開発してきました。この記事では、シンプルヘッジEAをさらに改良することに焦点を当てます。私たちの目標は、数学的分析と総当り攻撃アプローチを組み合わせて、この取引戦略を実行する最も効果的な方法を見つけることによって、そのパフォーマンスを向上させることです。

このディスカッションでは、主にシンプルヘッジ戦略の数学的最適化に焦点を当てます。複雑で深い分析が必要なため、数学的最適化とそれに続くコードに基づく最適化の両方を1つの記事で取り上げるのは現実的ではありません。したがって、この記事では数学的な側面に焦点を当て、最適化プロセスの背後にある理論と計算を徹底的に探ります。次回以降の連載では、最適化のコーディングの側面に焦点を移し、ここで確立した理論的基礎に実践的なプログラミング技術を応用していきます。

今回取り上げる予定の内容は以下の通りです。

1. 最適化を深く掘り下げる：より詳しく
2. 数学的最適化
3. 結論

最適化を深く掘り下げる：より詳しく

最適化と言えば、何を思い浮かべるでしょうか。この言葉は広範であると同時に複雑でもあり、しばしば、最適化とはいったい何なのかという疑問を投げかけます。

詳しく見てみましょう。その核心において、最適化とは、デザイン、システム、意思決定など、何かを最高レベルの完成度、機能性、有効性まで洗練させる行為、プロセス、方法論を指します。しかし、現実を直視しましょう。絶対的な完璧さを達成することは、むしろ理想主義的な追求です。本当の目標は、今ある資源で可能なことの限界に挑戦し、可能な限り最高の結果を得るために努力することです。

より深く掘り下げると、最適化の領域は広大で、私たちが自由に使える方法は無数にあることがわかります。この議論の文脈では、「古典的なヘッジ戦略」に焦点を当てます。数ある最適化テクニックの中でも、2つの傑出したアプローチが私たちの探求の要となるでしょう。

1. 数学的最適化：このアプローチでは、数学の力を最大限に利用します。利益関数やドローダウン関数などを作成し、これらの構成要素を使用して、確かで定量化可能なデータに基づいて戦略を微調整できることを想像してみてください。これは、最適化努力の精度を高めるだけでなく、戦略の有効性を向上させるための明確で数学的な道筋を提供する方法です。

2. 総当たり攻撃アプローチ：もう一方にあるのは総当り攻撃アプローチです。これは単純ですが、その範囲は大変なものです。この方法では、考えられるあらゆる入力の組み合わせをテストし、それぞれをバックテストして、可能な限り最良の設定を見つけます。目標は、戦略的優先順位に応じて、利益を最大化するか、ドローダウンを最小化することです。ただし、部屋の中の象、つまり圧倒的な数の入力の組み合わせを認めることは重要です。この複雑さゆえに、可能性のあるすべてのシナリオをバックテストすることは、特にリソースと時間が限られている場合には、至難の業となります。
   

2つのアプローチを組み合わせることの素晴らしさがここで明らかになります。はじめに数学的最適化を適用することで、総当たり攻撃をおこなうケースを大幅に減らすことができます。これは、最も有望な構成に集中できるようにする戦略的な作戦であり、総当たり攻撃プロセスがより管理しやすく、時間効率的になります。

要するに、最適化の旅とは、理論的な正確さと現実的な実現可能性のバランスをとることです。数学的最適化から始めることで、膨大な可能性の海をフィルタし、舞台を整えます。そして、総当たり攻撃に移行することで、残りの選択肢を厳密にテストし、改良することができます。これらの手法を組み合わせることで、古典的なヘッジ戦略を最も効果的に最適化するための強力なコンビが完成します。

数学的最適化

数学的最適化の世界に足を踏み入れる場合、最初のステップは明確で実行可能な枠組みを確立することです。つまり、成果（この場合は利益）に大きな影響を与える変数を明確にすることです。利益関数を形成する上で重要な役割を果たす構成要素を解剖してみましょう。

1. 初期ポジション(IP)：バイナリ変数で、1は買い、0は売りを表します。この最初の選択によって、取引戦略の方向性が決まります。
2. 最初のロットサイズ(IL)：取引サイクル内の最初の注文の大きさで、取引規模の基礎を築きます。
3. 利食い買い(BTP)：買い注文に対してあらかじめ設定された利益基準値で、ポジションを決済して利益を確保するタイミングの目標となります。
4. 利食い売り(STP)：同様に、これは売り注文の利益目標であり、売りポジションが利益を実現するために決済される時点を示します。
5. 売買距離(D)：買い注文レベルと売り注文レベルの間隔を定義する空間パラメータで、取引のエントリポイントに影響します。
6. ロットサイズ乗数(M)：この係数は、取引サイクルの進行に基づく動的な調整を導入し、後続の注文のロットサイズが段階的に増大します。
7. 注文数(N)：サイクル内の注文の総数で、取引戦略の幅を表します。

わかりやすくするために、これらのパラメータは簡略化された形で示されていますが、方程式の中では、これらの変数のいくつかは添え字表記で参照されることは注目に値します。

これらのパラメータを基礎として、利益関数の定式化を進めることができます。この関数の本質は、これらの変数を変化させることによって、利益（または損失）がどのように影響を受けるかを数学的に表現することです。利益関数は私たちの最適化プロセスの基礎であり、異なるシナリオのもとで異なる取引戦略の結果を定量的に分析することを可能にします。

では、利益関数のパラメータを書いてみましょう。

つまり、最終的な利益関数は次のようになります。

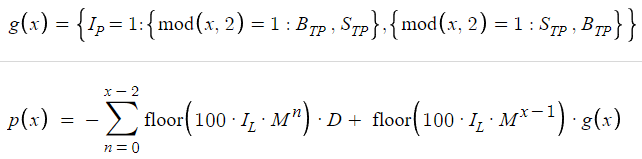
一見すると、利益関数は数式と記号で難解に見えるかもしれませんが、怖気づく必要はありません。方程式の各要素には特定の役割があり、それを分解することで、取引の枠組みの中でどのように利益が生み出されるかを包括的に理解することができます。

ここで、利益計算のダイナミクスを理解することが重要です。この理解の中心となるのは、p(x)で示される主な利益関数とそのコンポーネントであるg(x)の区別です。ここで、xは注文またはポジションの合計数を表します。この区別は、取引サイクルがxポジションにわたって完了したときにどのように利益が発生するかを理解するための基礎を築くものであり、極めて重要です。その本質を理解するために、この概念を体系的に分解してみましょう。

1つの注文で取引サイクルを終了することに決めたとします。このシナリオは次のように展開します。

この設定では、g(x)は注文数(N)と初期ポジション(IP)の間の相互作用に基づく値をとります。たとえば、初期ロットサイズ(IL)を0.01に設定し、この説明のためにNを1とし、初期ポジション(IP)が買いのアクション（すなわちIP = 1）を示すとすると、g(x)は利食い買い(BTP)の値をとります。その結果、利益関数p(x)は100×0.01×BTP＝BTPとなり、利益がBTPに等しいことを象徴的に示します。この図は重要な点を強調しています。私たちは利益を通貨ではなくpipsで計算しています。このアプローチは、異なる通貨間での利益計算を一般化し、口座タイプ（マイクロまたはスタンダード）に関係なく適用可能であることを保証し、全体的な計算を簡素化するために意図的に選択されています。ロットサイズを100倍にする根拠は単純です。これにより、ロットサイズを正確なpips値に変換することが容易になり、正確な利益計算に不可欠なステップとなります。

ここで、Nを2に増やし、新たな複雑さを導入するシナリオを考えてみましょう。

 

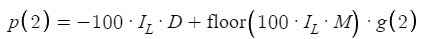
このわずかな調整で、利益計算が複雑になり、根本的な理由の深い探求を促します。これは例を通して最もよく説明されます。この複雑さの重要な要素はfloor関数の導入です。floorは学校で習う「最大整数関数(GIF)」を彷彿させる数学演算です。floor関数は特定の目的を果たします。任意の数値が与えられたとき、小数部を切り捨て、その前の最大の整数にするのです。正の値の場合、この操作は簡単で、floor(1.54) = 1、floor(4.52) = 4、といった具合です。このメカニズムは私たちの利益関数に不可欠であり、計算において整数値のみが考慮されることを保証するものです。これにより、正の値に焦点を当て続けることができ、このコンテキストで負の値を考慮する必要がなくなります。

この計算式の最初の部分は、インパクトレベル(IL)の-100倍としてfloorを計算することから始まります（ILが0.01の場合）。計算は-100×0.01、答えは-1となります。これを距離(D)と一緒にすると、式は取引戦略で説明したように、利益に結びつかなかった各取引のD pipsの損失を表します。次のステップは、100×IL×M（乗数）のfloorを、買いまたは売り注文の利食い(TP)値を表す関数g(x)に加算することです。ILとMの積が、その後の（2回目の）注文のロットサイズを決定し、この積に100を掛けることで、pipsの正確な計算が容易になります。

この方程式におけるfloor関数の必要性について、重要な疑問が生じます。明確にするために、ILが0.01、Mが2で、100×IL×M＝2が計算される例を考えてみましょう。この場合、2にfloor関数を適用すると2が得られるので、floor関数は冗長になるようです。ただし、floor関数の有用性は別のシナリオで明らかになります。ILが0.01のままでMが1.5に設定されている場合、ILとMの100倍の積は1.5に等しくなります。この時点で、証券会社は0.01の倍数のロットサイズを要求するため、結果として0.015のロットサイズが許されないことを理解することが重要です。この戦略によると、注文サイズは0.01に戻り、その後のロットサイズは証券会社の制限下で実行可能であることを保証するために制御された方法で増加します。例えば、0.01×1.5×1.5で計算される次のロットサイズは0.0225となり、実用上は事実上0.02に四捨五入されます。そのため、floor関数を使用して方程式をこの運用実態に合わせて調整し、0.01やそれに続く0.02のようなロットサイズが正確に表現されるようにします。この調整により、モデルは取引の実際的な制約を確実に反映し、戦略のガイドラインに基づくロットサイズの端数増加に対応するfloor機能の必要性を強調しています。最後に、この調整値に g(x)を掛けます。g(x)は買いのTPまたは売りのTPに対応し、取引戦略のパラメータを方程式の定式化にさらに統合します。この詳細な内訳は、方程式の各要素の背後にある論理的根拠を明確にし、その構成に内在する戦略的考察を強調するものです。

ここでNが3だとすると、利益が出ます。

Nを3に設定したシナリオでは、計算式は特定の条件下で利益が出る状況を示しており、その結果、Nで示される注文数に基づいて結果を計算する構造的なアプローチとなります。最初のセグメントは一貫性を保っており、最初の注文での損失を表します。2つ目のセグメントは、g(x)をDに置き換えることで、このアプローチを適応させています。3つ目のセグメントの違いはM^2の導入に伴い、乗数効果が指数関数的に増加することを示していますが、これは文脈を考えると簡単です。

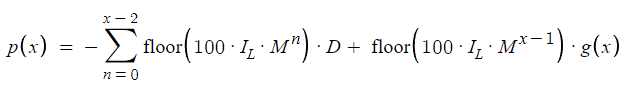
この枠組みをNの異なる値について拡張し、この取引戦略のダイナミクスを包括的に包含する一般化された方程式を提示します。この式は、Nの異なるインスタンスに適応可能であり、注文数の増加に伴う進行と潜在的な結果を理解するための基本モデルとして役立ちます。

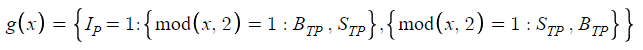
利食い買い(BTP)と利食い売り(STP)を交互に繰り返すg(x)の決定は、初期ポジション(IP)とNのパリティに依存します。この二者択一の決定プロセスは、結果がIPとNの数値特性(偶数か奇数かに重点を置く)の両方に影響される条件構造にエレガントに要約されます。このメカニズムにより、市場ポジションと注文順序に基づく戦略目標に沿ったg(x)値の論理的割り当てが保証されます。

グラフ作成ツールであるDesmosを使用することで、リアルタイムでパラメータを調整することができます。変化に対する即時フィードバックを通じて理解を深めることができるため、この方程式を容易にインタラクティブに探求できるようになります。整数特有の結果を表示するこのツールの機能は、注文数が本質的に離散的な変数である実践的な状況において特に価値があります。

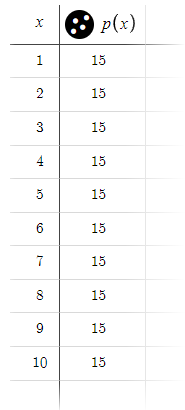
Desmosの事前定義されたパラメータによるデモは、標準的な条件下でのモデルの動作を示し、最大10注文の範囲にわたって15 pipsの一貫した利益が期待できることを明らかにしています。

注：分かりやすくするために、ここではスプレッドは無視しました。

結果を観察すると、この戦略に投資したいという欲求が生まれるかもしれませんが、慎重に行動し、決断を急がないことが肝要です。前に進む前に、まだ解決すべき多くの課題や問題が残っています。状況をより包括的に理解するためには、この表に追加の列を導入することが有益でしょう。その前に、この新しい列を支える方程式を少し考えてみましょう。この準備段階によって、データを分析するための明確で構造化されたアプローチが保証され、より多くの情報に基づいた意思決定プロセスが可能になります。

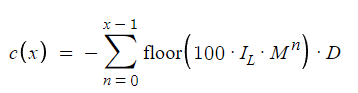
この式は、最大可能ドローダウンを示しています。明確にしておくと、10回目の注文でサイクルが終了した場合、最大ドローダウンは、10回目の注文が負けトレードになっていた場合の損失に極めて近い金額となります。これは、nが0からx-1まで進むという式で示されます。以前は、nが0からx-2まで進むと、利益が出る前に損失が発生していました。

この方程式は、潜在的な最大ドローダウンを定義するものであり、この戦略におけるリスクを理解する上で極めて重要な概念です。例えば、サイクルが10回目の注文で終了したとします。この文脈では、最大ドローダウンは、10回目の注文が損失をもたらした場合に発生する損失に近い金額と考えることができます。ドローダウンの計算は、0からx-1まで反復する変数nによって方程式内にカプセル化されます。このセクションでは、ドローダウンの計算に使用する範囲を指定します。これは、nが0からx-2までの範囲を通過し、その後に利益が続くという、以前の損失計算方法とは異なるものです。方程式のパラメータを調整することで、潜在的な利益が実現する前に起こりうる最大の損失シナリオを考慮することができ、戦略のリスクプロファイルをより正確に表現することができます。

デフォルトの入力パラメータを用いて可能な最大ドローダウンを決定するために、新しく導入した変数の値がxの変化によってどのように調整されるかを注意深く観察します。このステップは、xを変化させることが潜在的なドローダウンに与える直接的な影響を理解する上で極めて重要であり、私たちの戦略の下での様々なシナリオに関連するリスクについての洞察を提供します。

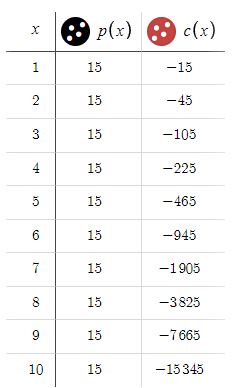
10回目の注文で勝ってサイクルを終了した場合、最大ドローダウンは15,345米ドルとなります。この数字は、特に15米ドルという比較的控えめな報酬と対比すると、かなり大きなものです。これらのダイナミクスを考慮して、BTPとSTPを15 pipsから50 pipsに増やしましょう、

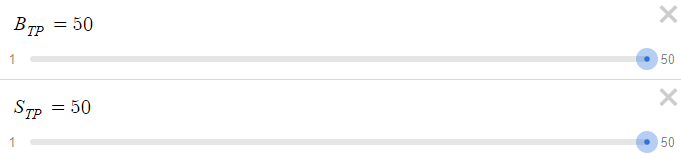
次に、それがどうなったか見てみましょう。

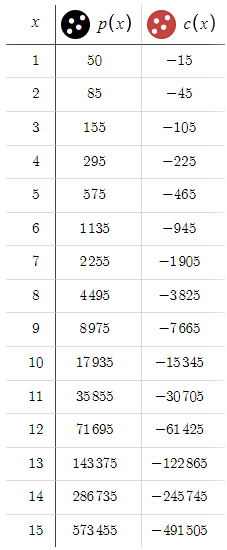
これは、損失が指数関数的に増加していた以前のシナリオからの大きな変化です。今、私たちは一貫して利益を上げており、非常に有利なリスクリワード比がハイライトされています。このような有望な結果を見ると、なぜ目標を50 pipsに限るのかという疑問が生じます。狙いを100 pipsまで広げる可能性を探ってみましょう。

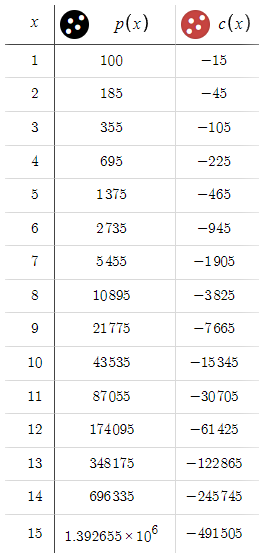
c(x)の値は変わりませんが、p(x)はすべてのxの値で増加しています。この格差は、潜在的な利益が損失を大きく上回っていることを考えれば、誰の目にも明らかでしょう。しかし、その根底にある罠には疑問を抱かざるを得ません。これを解明するために、BTPとSTPの両方を例えば10,000 pipsに設定した場合を考えてみましょう。このような状況では、価格が目標に到達するまでに永遠に時間がかかるでしょう。BTPとSTPが高ければ高いほど、サイクルを完了する可能性（つまりBTPかSTPのどちらかに到達する可能性）は低くなります。要するに、これは、xが与えられたときにサイクルが完了する確率を表す隠し要素「p」を導入したものです。BTPとSTPを無差別に増加させるとpが減少し、pが低いほどサイクルが完了する可能性が低くなります。したがって、利益の可能性にかかわらず、pが最小であれば、期待される利益は実現しない可能性があります。100 pipsの変動がすでに大きいEURUSDを主に扱っているため、BTP、STPともに50 pipsの仮制限を適用しています。この上限は直感に基づくもので、リスクとリターンのバランスを効果的にとるために必要に応じて調整することができます。

pを計算し、期待利益を算出するのは複雑な課題です。数学的最適化は構造化されたアプローチを提供しますが、それだけではp（サイクル完了の確率）を決定することはできません。より詳細に理解するにはチャート分析が必要です。pは本質的に不安定であり、確率変数として振る舞うため、さらに複雑な問題が生じます。pは確率値のベクトルを表し、各要素は一定の注文総数後にサイクルが終了する確率を示すことを認識することが重要です。例えば、ベクトルの最初の要素は、1つの注文だけでサイクルを完了する確率を表し、このロジックは、異なる注文の合計のための他の要素に拡張されます。この概念の包括的な検証、特にその応用と意味合いは、本連載で次回コードベースの最適化に移行する際の重要な焦点となります。

私たちの分析では、スプレッドという重要な要素を見落としていました。スプレッドは私たちの戦略において極めて重要な役割を果たし、利益と損失の両方に影響を与えます。これを考慮するため、p(x)とc(x)の両方からある項を引いて計算を調整し、スプレッドを分析に含めます。

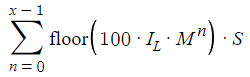
ここで重要なのは、調整がゼロからx-1までのすべての取引を考慮に入れていることであり、スプレッドは利益が出ているかどうかにかかわらず、すべての取引に影響を与えるということを認識していることです。分かりやすくするために、現在はスプレッド（Sと表記）を一定値として扱っています。これは、スプレッドの変動という付加的な変動要因によって数学的分析が複雑になるのを避けるための決定です。このように単純化することで、モデルの現実性は制限されるものの、過剰な複雑さに悩まされることなく、戦略の核心部分に集中することができます。

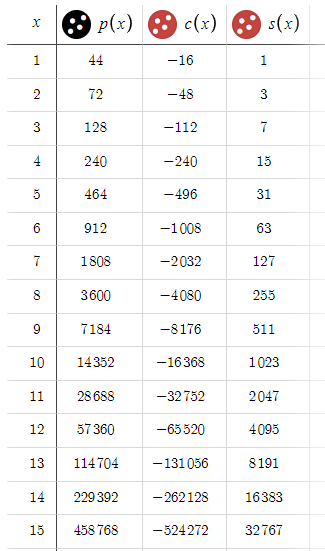
さて、s(x)を計算に導入したので、スプレッドが利益に与える実際の影響を定量化します。その影響はかなり大きく、xが大きくなるにつれてスプレッド関連の損失は段階的に増大し、最大32,000 pips、約3,200ドルに達する可能性があります。この調整によって、潜在的な利益がs(x)だけ減少するだけでなく、潜在的な損失も同じだけ増加し、リスクとリターンの比率が大きく変化します。この変化は、戦略的プランニングにおいてスプレッドを考慮することの重要性を浮き彫りにし、ヘッジ戦略を最適化する上でこの要素を注意深く管理する必要性を強調しています。

最後の課題である「総当り攻撃のケースを減らす」というのは、戦略にとって有益な結果が得られそうもない特定のパラメータの組み合わせを選択的に排除するプロセスを指しています。このステップは、私たちのアプローチを最適化する上で非常に重要です。特にコードベースの最適化を準備する際には、最も有望な構成の探索に計算資源を集中させることができるからです。

たとえば、BTP（買いトリガーポイント）、STP（売りトリガーポイント）、D（距離）のパラメータをすべて15に設定し、M（乗数）を1.5に設定したシナリオを考えてみましょう。

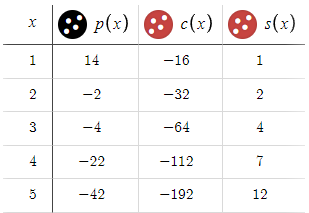
これらの設定の結果を分析すると、このようなパラメータでは満足のいく結果が得られないことがすぐにわかります。したがって、これらの具体的な値を戦略に取り入れたり、さらなる最適化を図ったりしても無駄であることは明らかです。

そこで問題になるのは、そのような効果のないパラメータの組み合わせをどのようにして事前に特定し、排除するかということです。私が最初にこれらのパラメータを発見したのは偶然でしたが、体系的にすべての最適でない入力を特定し、排除することは重要な課題です。そのためには、本格的な総当り攻撃最適化をおこなう前に、さまざまなパラメータセットの実現可能性を評価するための予備的分析を含む、方法論的アプローチが必要となります。こうすることで、最適化プロセスを合理化し、取引戦略の有効性を向上させることが期待できるパラメータの組み合わせのみを探索することに労力を費やすことができます。

最適化プロセスにおいて、最適でないパラメータの組み合わせを系統的に特定し、排除するという課題に取り組むことは複雑な作業です。本連載で次回以降に取り組むことになります。このアプローチにより、最も有望な戦略の集中的かつ効率的な探索が保証され、それによって取引手法の全体的な有効性が高まります。ということで、この話はここまでにして、次の部分に続きます。

結論

連載3回目となる今回は、シンプルヘッジ戦略の最適化について、数学的分析を中心に深く掘り下げ、次回おこなう総当り攻撃アプローチの基本的な考え方を得ることから始めました。

今後、本連載では、理論的な探求から実践的なコードベースの最適化へと移行し、これまでに得られた原理と洞察を実際の取引シナリオに適用していきます。このシフトは、リスクを効果的に管理しながらリターンを最大化しようとするトレーダーに、具体的な改善と実行可能な戦略を提供し、当社の戦略をより鮮明にすることを約束するものです。

本連載を通して、読者の皆さんの参加と意見は非常に貴重なものでした。私たちが前に進むにあたり、引き続きご意見やご提案をぜひ共有してください。共に、単に取引戦略を最適化するだけでなく、市場のボラティリティや不確実性の試練に耐えうる、より多くの情報に基づいた効果的な取引判断への道を切り開いていきます。

ハッピーコーディング！ハッピートレーディング！