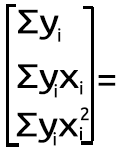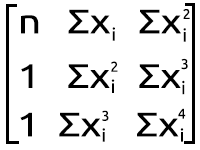
データサイエンスと機械学習（第07回）：:多項式回帰

目次：

• はじめに
• 多項式の復習
• 多項式の次数
• 多項式回帰
• 使用に適している場合
• ベイジアン情報量基準
• モデルの係数を見つける
• 最適なモデルを見つける
• 機能のスケーリング
• 多項式回帰の長所と短所
• 最後に

はじめに

回帰モデルはまだ終わっていません。少しの間戻ります。連載の最初の記事で述べたように、基本的な線形回帰は多くの機械学習モデルの基盤として機能します。今日は、多項式回帰として知られる、線形回帰とは少し異なるものについて説明します。

機械学習は多くの点で私たちの世界を大きく変えました。線形回帰、ロジスティック回帰、サポートベクターマシン、多項式回帰、およびその他の多くの手法など、分類および回帰問題の訓練データを学習するさまざまな方法があります。多項式回帰やサポートベクターマシンなどのいくつかのパラメトリック手法は、用途が広いことで際立っています。

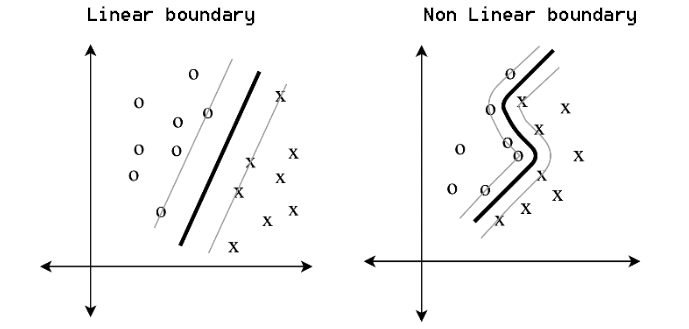
単純な問題では単純な境界、複雑な問題では非線形の境界が作成されます。

多項式の復習

多項式は、次のような数式です。

多項式01:

データxがあり、べき乗が増加し、データのスケーリングに使用されるいくつかの係数があります。

多項式回帰の別の例を次に示します。

多項式 02

5はa0、-7はa1、4はa2、11.3はa3に対応します。 

多項式では、必ずしもすべてのx項をここに含める必要はありません。この方程式を見てみましょう。

多項式03

それは次として考えることができます。

多項式の次数 

多項式には次数と呼ばれる別の概念があります。多項式の次数はnで表されます。これは、たとえば次のような数式で最も高い係数です。

1. 上記の多項式01は、n次多項式回帰です。
2. 上記の多項式02は、3次/次多項式回帰です。
3. 上記の多項式03は、3次/次多項式回帰でもあります。

2番目の方程式ではxを掛けた3つの変数があり、それらの係数は1、2、3の昇順であるのに対し、2番目の方程式では2つの変数しかないため、混乱する人もいます。多項式の次数は、主に式の最大係数によって決まります。

多項式回帰

多項式回帰は、予測をおこなうために使用される機械学習アルゴリズムの1つです。COVID-19やその他の感染症の蔓延率を予測するために広く使用されていると聞きました。このアルゴリズムが何で構成されているか見てみましょう。
単純な線形回帰モデルを見てみましょう。

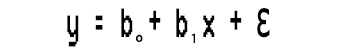
何か気づかれたでしょうか。

この単純な線形回帰は、一次多項式回帰に他なりません。多項式回帰に変数を追加できる順序によって異なります。たとえば、二次多項式回帰は次のようになります。

この式の位数はより高くできます。

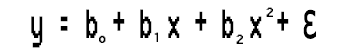
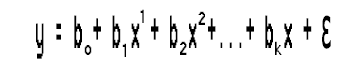
これはk次の多項式回帰です。ちょっと待ってください、これはまだ線形回帰ですか?線形モデルに何が起こったのでしょう。

線形性はどうなったのでしょうか。

以前の記事で、回帰は線形モデルに関するものだと言ったと思います。これらの二乗項係数がある場合、この多項式回帰を直線性に適合させるにはどうすればよいでしょうか。すべては、線形である必要があるものと非線形である必要があるものに帰着します。係数/ベータはすべて線形であり、より高いべき乗になるのはデータ自体だけです。

多項式回帰はいつ使用する必要があるのでしょうか。

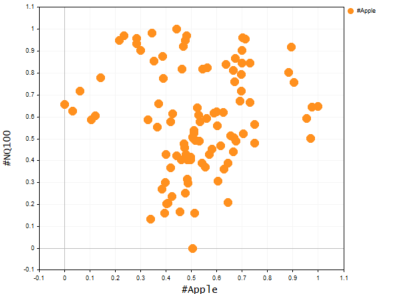
基本的な線形モデルが少し複雑なデータ(非線形)を適合したり、データセット内の複雑な関係を把握したりするのに適していないことは誰もが知っています。多項式回帰は、その問題を解決するためにここにあります。APPLEの株価を使用してNASDAQの価格を予測しようとすることを想像してみてください。AppleはNASDAQの価格の背後にある最大のインフルエンサーの1つであり、その関係はまだ線形ではないため、線形モデルは、将来の予測決定をおこなうために信頼できるまでにデータセットを適合させることができない可能性があります。価格値を表す散布図を作成して、これら2つの銘柄のグラフが同じ軸上でどのように見えるかを見てみましょう。

以下は、CGraphicsのおかげでターミナル上で散布図を作成する機能です(この記事を書いている瞬間まで、このようなことが可能であることを知りませんでした)。

bool ScatterPlot(
                 string obj_name,
                 vector &x,
                 vector &y,
                 string legend,
                 string x_axis_label = "x-axis",
                 string y_axis_label = "y-axis", 
                 color  clr = clrDodgerBlue,
                 bool   points_fill = true                 
                )
 { 
   if (!graph.Create(0,obj_name,0,30,70,440,320))
     {
       printf("Failed to Create graphical object on the Main chart Err = %d",GetLastError());
       return(false);
     }
   
   ChartSetInteger(0,CHART_SHOW,ChartShow);
   
   double x_arr[], y_arr[]; 
   
   pol_reg.vectortoArray(x,x_arr);
   pol_reg.vectortoArray(y,y_arr);
   
   CCurve *curve = graph.CurveAdd(x_arr,y_arr,clr,CURVE_POINTS);
   curve.PointsSize(10);
   curve.PointsFill(points_fill); 
   curve.Name(legend);
   graph.XAxis().Name(x_axis_label);
   graph.XAxis().NameSize(10);
   graph.YAxis().Name(y_axis_label);
   graph.YAxis().NameSize(10);
   graph.FontSet("Lucida Console",10);
   graph.CurvePlotAll();
   graph.Update();
 
   delete(curve);
   
   return(true);
 }

   string plot_name = "x vs y"; 
   
   ObjectDelete(0,plot_name);    
   ScatterPlot(plot_name,x_v,y_v,X_symbol,X_symbol,Y_symol,clrOrange); 

出力

Nasdaq対Appleのグラフ

この種の問題では線形モデルがうまく機能しないという事実を否定することはできないので、多項式回帰を試してみましょう。これによって、多項式モデルを作成するためにどの次数を使用すべきかという問題が提起されます。

モデル式

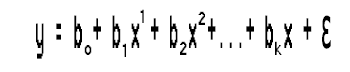
を見ると、独立変数は1つしかないので、累乗を任意にすることができます。またですが、この1つの独立変数をどの累乗にする必要があるかはどのように知ることができるのでしょうか。これを理解するには、まずBICと呼ばれるベイジアン情報量基準と呼ばれるものを理解するべきです。

ベイジアン情報量基準

式は次のとおりです。

BIC =  n log(SSE) + k log (n)

 n = データポイント数 

 k = パラメータの数

ただし、最適なモデルを見つける前に、基本的な多項式回帰を作成し、何がそれを動かしているのかを見てみましょう。そこから最適な次数を見つけることができます。

モデルの係数を見つける：

式

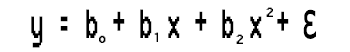
で、b0、b1、b2の値を見つけて、この2次多項式回帰タスクを解決しましょう。

次の連立方程式を使用します。

n = データポイント数

値を計算するには、この単純なデータセットを使用しましょう。

X	y
3	2.5
4	3.2
5	3.8
6	6.5
7	11.5

これで、問題に対する連立方程式のセットと、その上に構築するための単純なデータセットができました。値を簡単に入れて、関数電卓やMicrosoft Excelなどの好みのもので係数を見つけることができます。値;

• b0 = 12.4285714
• b1 = -5.5128571
• b2 = 0.7642857

が得られますが、MQL5ではこれはおこないません。上記の連立方程式のセットからメタエディタでこの結果を達成する方法を見つけて、行列形式に変換しましょう。

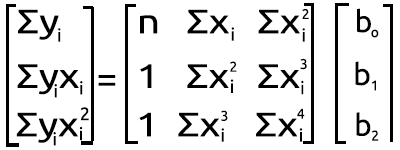多項式行列図

この乗算の結果は、連立方程式に戻るので、数学的に正しいことがわかります。

次に、コードを書いてみましょう。

多項式回帰クラス:

class CPolynomialRegression
  {
   private:
                        ulong  m_degree; //depends on independent vars
                        int    n;   //number of samples in the dataset
                        vector x;
                        vector y;
                        matrix PolyNomialsXMatrix; //x matrix 
                        matrix PolynomialsYMatrix; //y matrix 
                        matrix Betas;
                        double Betas_A[];  //coefficients of the model stored in Array

                        void   Poly_model(vector &Predictions,ulong degree);
                        
   public:
                        CPolynomialRegression(vector& x_vector,vector &y_vector,int degree=2);
                       ~CPolynomialRegression(void);
                        
                        double RSS(vector &Pred);               //sum of squared residuals
                        void   BIC(ulong k, vector &bic,int &best_degree);      //Bayessian information Criterion
                        void   PolynomialRegressionfx(ulong degree, vector &Pred);
                        double r_squared(vector &y,vector &y_predicted); 
                        
                        void   matrixtoArray(matrix &mat, double &Array[]);
                        void   vectortoArray(vector &v, double &Arr[]);
                        void   MinMaxScaler(vector &v);
  };

私たちのクラスは主にシンプルで、読むのに複雑なコードはありません。最初に変更が加えられた場合、コードは以下に添付されたファイルで更新されます。

上の多項式行列イメージ図の行列式から、各データポイントに独自の指数で発生した多くの合計があることがわかります。この計算は、右側の最初の配列のほぼすべての要素に対してオンデマンドでおこなわれるためです。-等号の側、以下はそれをおこなう方法の短いコード例です。

    vector c;
    vector x_pow;
    
    for (ulong i=0; i<PolynomialsYMatrix.Rows(); i++)
       for (ulong j=0; j<PolynomialsYMatrix.Cols(); j++) 
         {
            if (i+j == 0)  PolynomialsYMatrix[i][j] = y.Sum(); 
            else         
               {
                   x_pow = MathPow(x,i);       c = y*x_pow; //x vector elements are raised to the power i then the resulting vector is  
                                                                //Then multiplied to the vector of y values the output is stored in a vector c
                   PolynomialsYMatrix[i][j] =  c.Sum();     //Finally the sum of all the elements in a vector c is stored in the matrix of polynomials
               }
         }

上の多項式行列イメージ図の右側の行列を見ると、関数ΣxyとΣxy^2があることがわかります。これは少し異なるアプローチなので、その方法に関するコードも見てみましょう。

  
   double pow = 0;
   ZeroMemory(x_pow);
   
    for (ulong i=0,index = 0; i<PolyNomialsXMatrix.Rows(); i++)
       for (ulong j=0; j<PolyNomialsXMatrix.Cols(); j++, index++)
          {
             pow = (double)i+j; //The power corresponds to the access index of rows and cols i+j
             if (pow == 0) PolyNomialsXMatrix[i][j] = n;
             else          
                 {
                   x_pow = MathPow(x,pow); //x_pow is a vector to store the x vector raised to a certain power
                   
                   PolyNomialsXMatrix[i][j] =  x_pow.Sum(); //find the sum of the power vector
                 }
          }
    

多項式回帰にとって非常に重要であることが証明されたコードのこれらの合計行が得られたので、多項式行列図イメージの2番目の行列のように、これらの値を運ぶ行列を作成することから始めましょう。

等号の左側の行列から始めます。

    ulong order_size = degree+1;
    PolyNomialsXMatrix.Resize(order_size,order_size);
    
    PolynomialsYMatrix.Resize(order_size,1);
    
    vector c;
    vector x_pow;
    
    for (ulong i=0; i<PolynomialsYMatrix.Rows(); i++)
       for (ulong j=0; j<PolynomialsYMatrix.Cols(); j++) 
         {
            if (i+j == 0)  PolynomialsYMatrix[i][j] = y.Sum(); 
            else         
               {
                   x_pow = MathPow(x,i);       c = y*x_pow;
                   PolynomialsYMatrix[i][j] =  c.Sum(); 
               }
         }
    
   if (debug) Print("Polynomials y vector \n",PolynomialsYMatrix);

行列内の要素がどのように配置されているかを見るだけで、最初の要素だけがxの値に乗算されないことがわかります。残りはすべて、xの値に乗算され、それらが行列に配置される場所のインデックスで累乗されます。

方程式の焦点で配列を切り替えます

最初に分かるのは、このMatrix配列のサイズが、先ほど計算した左側のY行列/Matrixの2乗のサイズに等しいことです。また、x項の累乗は、行と列を見て、要素が行列内のどこに配置されているかに基づいています。この行列は2乗行列であるため、その列をそれぞれ2つのループで2回ループして構築する必要があります。以下のコードを参照してください。

    ulong order_size = degree+1;
    PolyNomialsXMatrix.Resize(order_size,order_size);
    
    PolynomialsYMatrix.Resize(order_size,1);
     
    vector x_pow;
    
//---
   
   PolyNomialsXMatrix.Resize(order_size, order_size);
   
   double pow = 0;
   ZeroMemory(x_pow);
   //x_pow.Copy(x);
   
    for (ulong i=0,index = 0; i<PolyNomialsXMatrix.Rows(); i++)
       for (ulong j=0; j<PolyNomialsXMatrix.Cols(); j++, index++)
          {
             pow = (double)i+j;
             if (pow == 0) PolyNomialsXMatrix[i][j] = n;
             else          
                 {
                   x_pow = MathPow(x,pow);
                   
                   PolyNomialsXMatrix[i][j] =  x_pow.Sum();
                 }
          }
  //---

   if (debug) Print("Polynomial x matrix\n",PolyNomialsXMatrix);
   

以下は、上記のコードスニペットの出力です。

CS      0       02:10:15.429    polynomialReg test (#SP500,D1)  Polynomials y vector 
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)  [[27.5]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)   [158.8]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)   [966.2]]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)  Polynomial x matrix
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)  [[5,25,135]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)   [25,135,775]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)   [135,775,4659]]

すばらしいです。さて、ここからがややこしいところです。ベータ値の未知の行列の値を見つけるには、行列に関するいくつかの数学を調べる必要があります。

乗算された行列の未知の値を見つける：

上記で値を取得したばかりの行列に対して、同じ手順に従います。

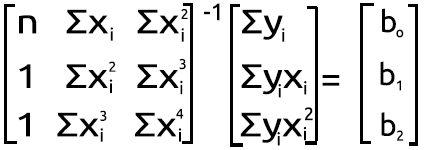
逆行列を見つけるプロセスは比較的単純で、行列の標準ライブラリを使用して1行ではないにしても2行のコードが必要です。

    PolyNomialsXMatrix = PolyNomialsXMatrix.Inv(); //find the inverse of the matrix then assign it to the original matrix 

最後に、モデルの係数を見つけるには、y値を合計した行列に逆行列を乗算する必要があります。

    Betas = PolyNomialsXMatrix.MatMul(PolynomialsYMatrix);

では、ベータ行列を印刷して、このプロセスから何が得られたかを確認します。

CS      0       02:10:15.429    polynomialReg test (#SP500,D1)  Betas 
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)  [[12.42857142857065]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)   [-5.512857142857115]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)   [0.7642857142856911]]

2次多項式回帰の係数が得られたので、それらに基づいてモデルを構築してみましょう。

void CPolynomialRegression::Poly_model(vector &Predictions, ulong degree)
 {
   ulong order_size = degree+1;
   Predictions.Resize(n);
   
   matrixtoArray(Betas,Betas_A); 
   
    for (ulong i=0; i<(ulong)n; i++)
     {
      double sum = 0;
       for (ulong j=0; j<order_size; j++) 
         {
           if (j == 0) sum += Betas_A[j];
           else        sum += Betas_A[j] * MathPow(x[i],j);
         }
       Predictions[i] = sum;
     }
 }

モデルのコードは単純に見えるかもしれませんが、少なくとも今のところは、必要なだけ多くの次数を処理できます。 x値とy値の同じ軸にモデル予測をプロットしてみましょう

   ObjectDelete(0,plot_name);
   plot_name = "x vs y";   
   ScatterCurvePlots(plot_name,x_v,y_v,Predictions,"Predictions","x","y",clrDeepPink);

bool ScatterCurvePlots(
                       string obj_name,
                       vector &x,
                       vector &y,
                       vector &curveVector, 
                       string legend,
                       string x_axis_label = "x-axis",
                       string y_axis_label = "y-axis", 
                       color  clr = clrDodgerBlue,
                       bool   points_fill = true                 
                      )
 {
 
   if (!graph.Create(0,obj_name,0,30,70,440,320))
     {
       printf("Failed to Create graphical object on the Main chart Err = %d",GetLastError());
       return(false);
     }
   
   ChartSetInteger(0,CHART_SHOW,ChartShow);
   
   
//--- additional curves

   double x_arr[], y_arr[]; 
   
   pol_reg.vectortoArray(x,x_arr);
   pol_reg.vectortoArray(y,y_arr);

   double curveArray[]; //curve matrix array
   
   pol_reg.vectortoArray(curveVector,curveArray);
   
   graph.CurveAdd(x_arr,y_arr,clrBlack,CURVE_POINTS,y_axis_label);
   graph.CurveAdd(x_arr,curveArray,clr,CURVE_POINTS_AND_LINES,legend);
    
//---

   graph.XAxis().Name(x_axis_label);
   graph.XAxis().NameSize(10);
   graph.YAxis().Name(y_axis_label);
   graph.YAxis().NameSize(10);
   graph.FontSet("Lucida Console",10);
   graph.CurvePlotAll();
   graph.Update();
   
   return(true);
 } 

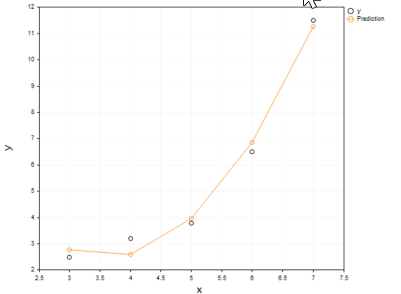
出力

多項式モデルが私たちのデータにうまく適合できたことは否定できません。この場合、データの適合において線形モデルよりも優れている可能性があります。

最適な多項式の次数を見つける

前に述べたようにベイジアン情報量基準は、最適なモデルを見つけるために使用するアルゴリズムです。数式をコードに変換しましょう。BICによれば、BICの値が最小のモデルが最良のモデルです。そのモデルは、残差/誤差の合計が最小のモデルだからです。

void  CPolynomialRegression::BIC(ulong k, vector &bic,int &best_degree)
 {
   vector Pred;
   
   bic.Resize(k-2); 
   best_degree = 0;
   
    for (ulong i=2, counter = 0; i<k; i++)
      {         
         PolynomialRegressionfx(i,Pred);         
         bic[counter] = ( n * log(RSS(Pred)) ) + (i * log(n));  
         
         counter++;
      }
      
//--- 

   bool positive = false;
   for (ulong i=0; i<bic.Size(); i++)
      if (bic[i] > 0) { positive = true; break; }
   
  
   double low_bic = DBL_MAX;
   
   if (positive == true) 
    for (ulong i=0; i<bic.Size(); i++) 
     {
      if (bic[i] < low_bic && bic[i] > 0) low_bic = bic[i];
     }
   else  low_bic = bic.Min(); //bic[ best_degree = ArrayMinimum(bic) ];
      
   printf("Best Polynomial Degree(s) is = %d with BIC = %.5f",best_degree = best_degree+2,low_bic);

 }

コードから、関数RSSは平方和の残差です。この関数は、二乗残差の合計を求めます。

double CPolynomialRegression::RSS(vector &Pred)
 {
  if (Pred.Size() != y.Size()) Print(__FUNCTION__," Predictions Array and Y matrix doesn't have the same size");
 
   double sum =0;
    for (int i=0; i<(int)y.Size(); i++)
      sum += MathPow(y[i] - Pred[i],2);
      
    return(sum);
 }

この関数を実行して、10次の中から最適な多項式を見つけます。

   vector bic_; //A vector to store the model BIC values for visualization purposes only
   
   int best_order; //A variable to store the best model order 
   
   pol_reg.BIC(polynomia_degrees,bic_,best_order);

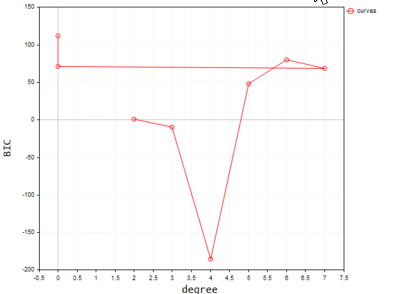
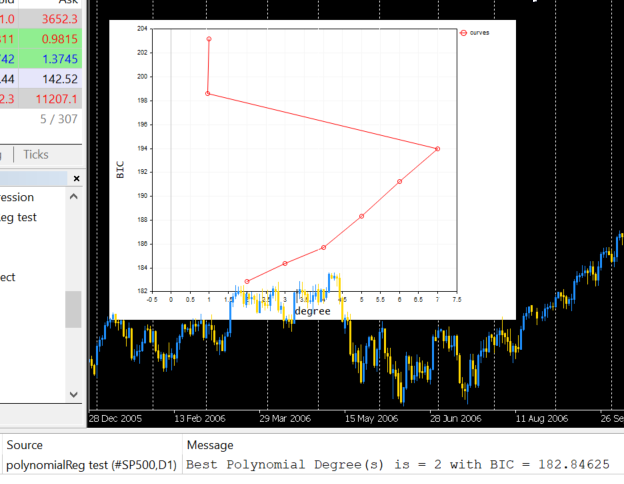
以下は、ターミナルにプロットしたときの出力です。

コードによると、最適なモデルの多項式次数は2です。次数2のモデルが、この単純なデータセットに最適であることは否定できません。

2022.09.22 20:58:21.540 polynomialReg test (#NQ100,D1)  Best Polynomial Degree(s) is = 2 with BIC = 0.93358

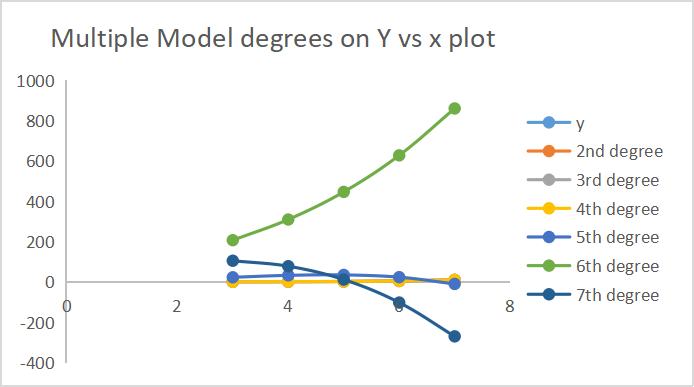
以下は、各モデルがどのように予測をおこなったかの出力です。

次数出力の7つが同じ軸にプロットされています。

機能のスケーリングは不可欠

多項式回帰では、任意のべき乗にできる独立変数が1つしかないため、最初に機能をスケーリングする必要があります。独立変数がこれらの機能の100-1000の範囲、2次で10000-1000,000の範囲で、3次で10^6-10^9の範囲になる場合、これは非常に重要になります。これは多量です。

データセットをスケーリングする方法とアルゴリズムは多数ありますが、最小-最大スケーラー関数を使用してベクトルをスケーリングします。このプロセスは、データセットを操作する前に実行する必要があることに注意してください。以下は、データセットからベクトルをスケーリングするために使用される関数のコードです。

void MinMaxScaler(vector &v)
 {
   //Normalizing vector using Min-max scaler
   
   double min, max, mean;
   min = v.Min();
   max = v.Max();
   mean = v.Mean();
   
   for (int i=0; i<(int)v.Size(); i++)
     v[i] = (v[i] - min) / (max - min);  
   
 } 

必要なものがすべて揃ったので、ライブ市場データに基づいてモデルを構築する時が来ました。上記のNasdaqとAppleのグラフを参照してください。結果を得るには、いくつかの手順を踏む必要があります。

市場価格データの抽出とスケーリング：

   if (!SymbolSelect(X_symbol,true))   printf("%s not found on Market watch Err = %d",X_symbol,GetLastError());  
   if (!SymbolSelect(Y_symol,true))    printf("%s not found on Market watch Err = %d",Y_symol,GetLastError());  
  
   matrix rates(bars, 2);
   vector price_close;

//---

   vector x_v, y_v;

   price_close.CopyRates(X_symbol,PERIOD_H1,COPY_RATES_CLOSE,1,bars); //extracting prices
   
   rates.Col(price_close,0);
   
   x_v.Copy(price_close);

//---
   
   price_close.CopyRates(Y_symol,PERIOD_H1,COPY_RATES_CLOSE,1,bars);
   
   y_v.Copy(price_close);
    
   rates.Col(price_close,1);
   
//---

   MinMaxScaler(x_v); //scalling all the close prices
   MinMaxScaler(y_v); //scalling all the close prices

//---

以下は、散布図に表示された出力です。

02：Bic関数を使用して最適なモデルを見つける

//--- FINDING BEST MODEL USING BIC
   
   vector bic_; //A vector to store the model BIC values for visualization purposes only
   
   int best_order; //A variable to store the best model order 
   
   pol_reg.BIC(polynomia_degrees,bic_,best_order);
   
   ulong bic_cols = polynomia_degrees-2; //2 is the first in the polynomial order 
   
//--- Plot BIc vs model degrees

   vector x_bic;
   x_bic.Resize(bic_cols);  
   for (ulong i=2,counter =0; i<bic_cols; i++)  {   x_bic[counter] = (double)i;   counter++;   }     
    
   ObjectDelete(0,plot_name);
   plot_name = "curves";
   ScatterCurvePlots(plot_name,x_bic,y_v,bic_,"curves","degree","BIC",clrBlue);
   Sleep(10000);

以下は出力です。

最後に 

これで、最適なモデルの次数は2であることがわかりました。2度のモデルを作成し、それを使用して値を予測し、最後にグラフに値をプロットします。

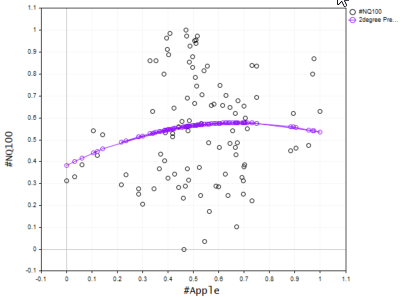
   vector Predictions;
   pol_reg.PolynomialRegressionfx(best_order,Predictions); //Create model with the best order then use it to predict
   
   ObjectDelete(0,plot_name);
   plot_name = "Actual vs predictions";   
   ScatterCurvePlots(plot_name,x_v,y_v,Predictions,string(best_order)+"degree Predictons",X_symbol,Y_symol,clrDeepPink);

結果のプロットを以下に示します

モデル精度の確認

モデルに最適な次数を見つけたにもかかわらず、予測精度を確認して、そのモデルがデータセット内の関係をどのように理解できるかを知る必要があります。

   Print("Model Accuracy = ",DoubleToString(pol_reg.r_squared(y,Predictions)*100,2),"%");

出力

2022.09.30 16:19:31.735 polynomialReg test (#SP500,D1)  Model Accuracy = 2.36%

悪いニュースは、最悪のモデルの中で悪いモデルを手に入れたということです。多項式回帰を使用して特定のタスクを解決することを決定する前に、多項式回帰にはその基礎として線形モデルがあるため、常に相関するデータがあることを覚えておいてください。線形相関である必要はありませんが、約50%の相関がある可能性があります。理想的には、NASDAQとAPPLEのデータセットを振り返ってその相関関係を確認すると、1%未満の相関係数が得られました。これがおそらく、このデータセットから適切なモデルを取得できなかった理由です。 

   Print("correlation coefficient ",x_v.CorrCoef(y_v));

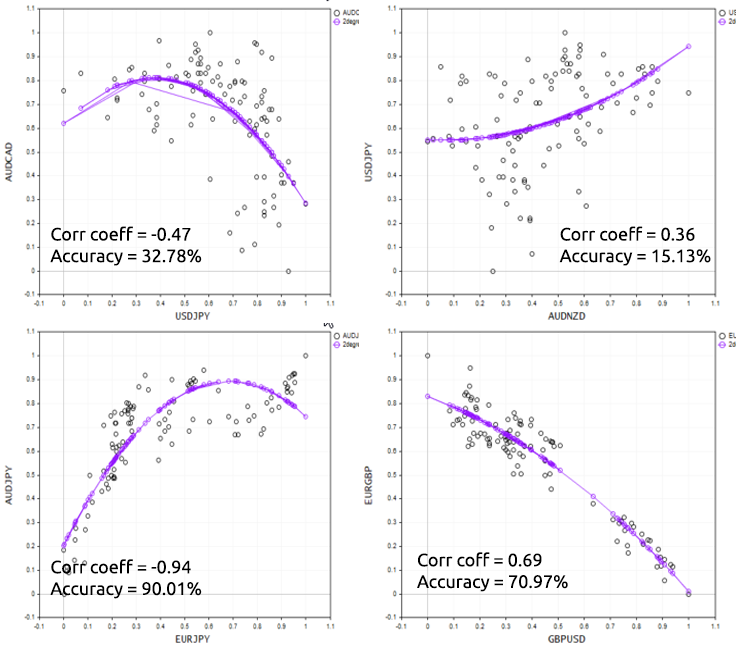
この点をうまく説明するために、さまざまな外国為替商品でスクリプトを試してみましょう。

多項式回帰の長所と短所

長所：

• 変数間の非線形関係をモデル化できる
• 適合に使える機能が豊富
• 探索目的に適している。さまざまな多項式の次数/次数をテストして、所有しているデータセットに最適なものを確認できる
• コード化して結果を解釈するのが簡単かつ強力

短所：

• 外れ値が結果を著しく台無しにする可能性がある 
• 多項式回帰モデルは過剰適合しがち（疑いなし）
• 過剰適合の結果として、モデルが外部データで機能しない可能性がある

最後に

独立変数と従属変数の間の関係が線形であるとは想定されていないため、多項式回帰は多くの場合に役立つ機械学習手法です。さまざまなデータセットを操作する際の自由度が高まり、線形モデルができるギャップを埋めるのに役立ちます。この手法は、線形モデルがデータに適合していない場合に適しています。このパラメトリックモデルは非常に柔軟であるため、訓練されていないデータ/テストデータではパフォーマンスが非常に悪い可能性があるため、過剰適合に注意することが重要であると言われています。モデルの次数を最も低くして、モデルにミスの余地を与えることをお勧めします。 

ご精読ありがとうございました。

配列形式の行列に関する詳細情報>>行列とベクトル

参考文献|書籍

• パターン認識のためのニューラルネットワーク（計量経済学の高度なテキスト）
• ニューラルネットワーク：取引の秘訣（コンピュータサイエンスの講義ノート、7700）
• 深層学習（適応計算と機械学習シリーズ）

記事の参照

• データサイエンスと機械学習（第01回）： 線形回帰
• データサイエンスと機械学習（第02回）：ロジスティック回帰 
• データサイエンスと機械学習（第03回）：行列回帰
• データサイエンスと機械学習（第06回）：勾配降下法