Комбинаторика и теория вероятностей для трейдинга (Часть I): Основы

Содержание

• Введение
• Чем может быть полезна теория вероятностей при анализе рынка?
• Нюансы прикладной теории вероятностей для ручной и автоматической торговли
• Деревья вероятностей и гипотезы
• О фракталах
• Схема Бернулли
• Создаем первый фрактал
• Выводы
• Заключение

Введение

На мой взгляд, язык теории вероятностей как никакой другой способен открыть перед трейдером совсем иной уровень понимания происходящих процессов внутри рынка. Овладев тонкостями и нюансами теории вероятностей, вы в первую очередь начнете мыслить совсем другими категориями. "Кажется" или "кто-то сказал, что надо вот так" уже не будут вызывать в вашем мозге какие-то ложные рефлексы или желание сломя голову торговать на реальном счету. С другой стороны, я понимаю, что для многих данный подход чужд, в первую очередь потому, что многие живут совсем в иной парадигме, которая им комфортна. Хочу немного растрясти вас и показать настоящий и правильный подход к торговле. Во главе всего должны быть цифры и только, и никаких "может быть", "если", "мне кажется" и "что если".

Чем может быть полезна теория вероятностей при анализе рынка?

Стоит отметить, что я достаточно большой промежуток времени в своей жизни очень тесно занимался техническими науками, и теория вероятностей давалась труднее всего. Причиной тому служило то, что я не понимал, насколько широки ее возможности. Неоспоримым плюсом является безграничная широта ее возможностей, которая зависит лишь от вашей смекалки и усердия, ну и интеллекта, конечно же. Хочу отметить, что спустя годы изучения технических дисциплин я понял, что интеллект не состоит в быстродействии выполнения однотипных операций или внимательности, а как раз показывает гибкость вашего ума. Если взять, к примеру, дифференциальную математику, теорию векторных и скалярных полей, да даже школьную алгебру, там везде есть некоторый набор правил или рекомендаций, следуя которым можно решить практически любую задачу. Как только задача начинает выходить за рамки стандартных, наш мозг встает в ступор и не понимает, что делать. В теории вероятностей таких моментов максимум, но как раз благодаря этому решение многих задач может быть обеспечено только совершенно разными подходами. Иными словами, интеллект можно развить только усердием и несгибаемой волей к решению поставленной задачи, и теория вероятностей поможет вам в этом.

В рамках теории вероятностей описываются такие краеугольные понятия торговли, как математическое ожидание, всевозможные вероятности различных событий, различные усредненные величины, а также проценты и многое-многое другое. Теория вероятностей учит нас, что не существует идеальной торговой системы, и каждая система имеет свои риски. В наших силах лишь подобрать ту торговую систему, риски которой у нас не будут вызывать дискомфорт. Но самое главное — правильно интерпретировать данные риски. Иными словами, мы уходим от неточного языка ощущений или визуальных приблизительных оценок к четким количественным критериям. Визуальные, конечно, тоже нужны, но они лучше работают в тандеме с количественными показателями. Все тонкости и нюансы невозможно описать в одной статье, но кое-что интересное я вам покажу в данной статье. Уверен, даже те, кто не чужд математике, найдут что-то для себя.

Нюансы прикладной теории вероятностей для ручной и автоматической торговли

Для того чтобы правильно использовать теорию вероятностей для анализа рынка, нужно в первую очередь познакомиться с событиями и их вероятностями. Событие представляет собой набор исходов, которые удовлетворяют каким-либо критериям, либо группируются по какому-либо признаку в обособленный набор. Исходом называется некий элементарный элемент, который равноправен всем остальным в данной группе. Группой называют все возможные исходы какого-либо процесса. Не так важно, что это за процесс, какова его физика или как долго этот процесс протекает, самое главное, что при полном протекании процесса мы получим какой-то результат или что-то, чего не было до того, как процесс еще не был завершен. Те исходы, которые относятся к нашему событию, по сути и являются нашим событием, просто мы для удобства восприятия объединяем их в некий единый объект. Можно условно изобразить сказанное на рисунке:

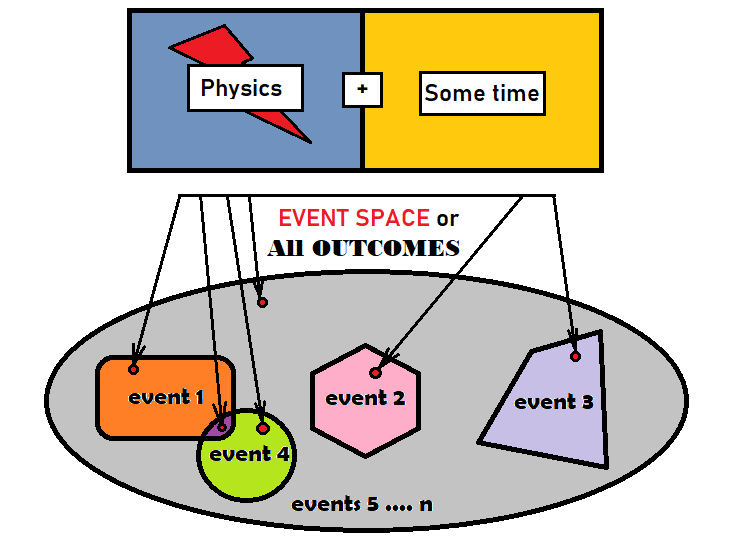
Серый эллипс здесь играет роль всех исходов и его в математике принято называть "пространством событий". Это не значит, что пространство событий имеет геометрическую форму, просто для описания данных понятий вполне подходит плоскость. Я изобразил внутри эллипса 4 разных события. Как видно из рисунка, внутри каждого события есть по одной небольшой красной точке. На самом деле этих точек может быть как ограниченное количество, так и бесконечное, все зависит от того, какой процесс мы рассматриваем. Также на рисунке есть два события, которые пересекаются. Такие события называются "совместными". Они так называются, потому что есть такие исходы, которые принадлежат обоим событиям. Остальные события являются "несовместными", поскольку они находятся в разных частях эллипса и не пересекаются геометрически. Всю остальную область серого цвета можно считать последним событием, либо также можно разбивать на более мелкие части до тех пор, пока серых зон не останется.

У каждого события обязательно есть как минимум одно соответствующее ему число, которое принято называть "вероятностью". Вероятность означает, насколько часто появляется выбранное событие в процессе повторения одного и того же процесса, если бы мы могли производить один и тот же опыт бесконечно. Есть два вида пространства событий:

1. С конечным числом возможных исходов
2. С бесконечным числом возможных исходов

В случае конечного числа возможных исходов вероятность можно посчитать так:

• P = S/N , S — количество исходов, которое попадает под критерии события, N — общее количество всех исходов пространства событий

В некоторых случаях, когда количество исходов в конкретном пространстве событий бесконечно, можно также определить данную вероятность например, с помощью интегралов. Конкретно, в случае нашего рисунка, величины "S" и "N" можно заменить на площади их геометрических фигур.

Не всегда получается явно определить, что из себя представляет пространство событий, как и не всегда получается явно определить, сколько в нем исходов и что за физику они описывают. Данные графические представления лишь призваны помочь провести аналогии нашему мозгу, чтобы он начал работать уже не какой-то геометрией и не пытался понять, что и зачем, а свыкся с мыслью, что работаем мы исключительно с вероятностями и дополнительными числами, которые соответствуют этим вероятностям. Еще события можно назвать "состояниями". Если использовать логику состояний, то получается, что вероятность есть не что иное, как частота появления определенного состояния в результате повторения одинаковых опытов. 

Если продолжить логику площадей фигур, то выходит, что сумма площадей всех фигур входящих в эллипс, в точности равна площади этого эллипса. Если уже переходить на язык математики, то площадь — это количество исходов, которые туда попадают. Вот и выходит что:

• N = S[1] + S[2] + ... + S[n]
  
• S — количество исходов конкретного события
• N — все исходы пространства событий

Если разделить обе части равенства на величину "N", то мы получим интересное и очень важное соотношение, которое лежит в основе всей теории вероятностей:

• 1 = S[1]/N   +   S[2]/N   +   ...   +S[n]/N

Хочу только уточнить, что данное соотношение работает только для тех событий, которые несовместны, потому что если события совместны, то площади фигур уже начинают накладываться друг на друга, и их суммарная площадь уже будет больше, чем площадь исходного эллипса. Все мы собирали паззл в детстве, так вот понятно, что площадь всех ячеек пазла в точности равна площади той картинки, что у нас получается в итоге. В данном случае кусочек пазла олицетворяет одно из событий. Двигаясь дальше, понятно, что все эти дроби не что иное, как вероятности конкретных событий:

• 1  = P[1]   +   P[2]   +   ...   +P[n]

От этого соотношения и произрастает термин "полная группа событий". Полной группой событий называется совокупность всех несовместных событий, которые образуют некоторое пространство событий. В случае пазла полной группой являются все кусочки пазла. Суммарная вероятность всех этих событий должна быть обязательно равна единице, что означает, что обязательно в результате опыта должно произойти какое-то из этих событий. Мы не знаем какое именно, но узнаем по результатам опыта.

Если хорошенько подумать, то можно понять, что в качестве события может выступать любой набор исходов из выбранного пространства событий. Это означает, что полную группу можно собрать всеми возможными способами и комбинациями. В случае конечного числа исходов таких комбинаций может быть ограниченное количество, а в случае бесконечного числа — бесконечное количество. Если известно, что количество исходов равно бесконечности, то математики переходят к рассмотрению такого понятия, как "случайная величина". В некоторых случаях даже удобно оперировать случайными величинами, потому что задача позволяет это сделать. Случайная величина — это уже немного другой способ описания пространства событий. В данном случае исходом является четкий набор из одного или более чисел, можно сказать что это вектор. В рамках данной модели рассмотрения вводится понятие "плотности вероятности". 

Я думаю, что стоит хотя бы поверхностно рассмотреть данные понятия, поскольку они нам понадобятся в дальнейшем при рассмотрении остального материала и для какого-то понимания с нашей стороны. Плотность вероятности — это функция, которая описывает сразу все пространство событий. Размерность этой функции в точности равна количеству чисел, которые необходимы для описания каждого исхода в данном пространстве событий. Например, если мы рассматриваем задачу стрельбы по мишени в тире, то размерность данной функции будет равна двум, потому что мишень плоская и олицетворяет собой двумерное пространство. В данном случае характеристиками конкретного исхода будут координаты X,Y. Данные числа и являются нашими случайными величинами и теперь мы можем записать:

• R = R(X,Y)
• R — плотность вероятности попадания пули в точку с координатами (X,Y)

Свойства данной функции таковы, что полный интеграл от минус до плюс бесконечности по всем переменным этой функции будет равен единице, что по сути отражает то же самое тождество, что было выше. Вероятности здесь определяются только интегралами по той области, где представлена функция и никак иначе. Из кусочно интегрированных областей можно составлять различные события, и при желании можно описать столько событий, сколько нам нужно, ведь их число равно бесконечности. В рамках данной статьи нам хватит и этого определения для понимания дальнейших мыслей, и я думаю, не стоит погружаться дальше, ведь там уже пойдут гораздо более серьезные вещи, которые в рамках наших задач абсолютно бесполезны.

Хочу еще немного рассказать про совместные события. Данные события тоже очень важны для общего понимания картины в целом. Понятно, что с несовместными событиями все должно быть достаточно просто, а вот с совместными все сложнее. В рамках теории вероятностей приходится сталкиваться с такими вещами, как объединение или дробление событий, но нам ведь не нужно знать, как будет выглядеть данное дробление или объединение, нас интересуют только вероятности, которые получатся в результате данных преобразований. Для этого вводится понятие суммы, и произведения событий, а так же операция инвертирования. Данные операции означают не одно и то же, что в обычной математике, а кроме того они призваны оперировать только вероятностями. Вероятности совместных событий нельзя складывать, потому что в этом случае нарушается целостность группы. В целом эти 3 операции над исходными событиями способны описать все возможные события, которые можно составить из кусков исходных событий. На примере двух совместных событий могу показать как это будет выглядеть на плоскости:

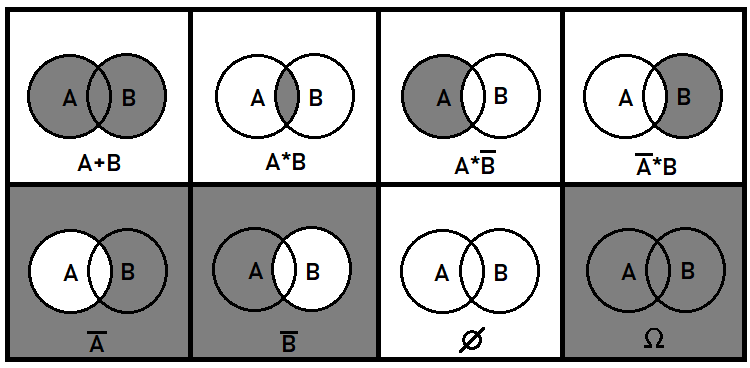
На самом деле можно придумать дополнительные алгебраические операции, но они могут быть составлены из уже представленных. Например, булево деление эквивалентно третьей и четвертой ситуации на рисунке, так как деление эквивалентно умножению на событие обратное выбранному. Вообще, строго говоря, для описания всех возможных событий, которые можно сконструировать из частей исходных событий, вполне достаточно первых двух случаев. В случае, когда совместны более двух событий, все становится гораздо сложнее. В этой статье мы пока что не будем оперировать совместными событиями, а только несовместными.

Математика рынка в первую очередь строится на таком понятии как "случайное блуждание". После того, как мы рассмотрим данное понятие, можно будет обобщить эти данные на случаи наличия закономерностей. Начнем с того, что предположим, мы открываем позицию с равноудаленными стоп-лоссом и тейк-профитом от цены открытия, и, если не учитывать спреды, комиссии и свопы этих позиций, если представить что позиция открывается бесплатно, то, думаю, всем очевидно, что, если случайно торговать в разных направлениях и в разных точках графика, то соотношение прибыль/убыток примет значение, равное единице. Иначе говоря, при бесконечной торговле количество прибыльных позиций будет в точности равно количеству убыточных. Из данного факта следует, что мы получаем нулевую прибыль, сколь угодно долго бы мы не торговали, а когда мы еще вычтем убытки от спредов, комиссий и свопов, то выйдет, что мы сливаем.

Многие могут подумать, а зачем мне знать что такое случайное блуждание и зачем мне вообще математика этого процесса, если я знаю что я в минусе как не крути? Случайное блуждание может помочь посчитать вероятности различных событий. Таких, как закрытие по асимметричным стопам или среднюю цену, которую пройдет график в определенном коридоре цен. Также и посчитать время жизни позиции и иные полезные показатели, которые, если и не дают ответ на вопрос, где войти  и где выйти, так однозначно вам помогут в оценке рисков или в вопросах максимизации или минимизации таких величин, как прибыль и убыток.

Деревья вероятностей и гипотезы

Очень полезным примером для развития ваших лобных долей будет такая штука, как деревья событий, или деревья вероятностей, кому как угодно. Данная тема берет начало из "cхемы Бернулли", потому что в основе всех вероятностных деревьев лежит именно она. Данная схема рассматривает цепочки несовместных событий, которые следуют друг за другом. Но перед тем как рассмотреть ее, мы рассмотрим "формулу полной вероятности". Именно изучая эту важнейшую конструкцию, можно придти к схеме Бернулли, а уже от схемы к вероятностным деревьям. Данная формула выглядит так:

• P(A) = Сумма(0 ... i .... n) [ P(H[i]) * P(A|H[i]) ] - вероятность события А
• P(H[i]) — вероятность возникновения гипотезы "H[i]"
  
• P(A|H[i]) — вероятность того что событие A произошло в рамках гипотезы "H[i]"

Отдельно хочу сказать, что когда мы имеем дело с вероятностями, лучше придерживаться правила писать их в стиле гипотез. К примеру, вот такая запись "P(H[k]|H[i]) " будет означать следующее:

1. Вероятность события "H[k]", вычисленная относительно пространства "H[i]"

Так сразу становится понятно, какое событие мы считаем пространством, а какое событие является вложенным. Все дело в том, что, по сути, каждое событие является другим более маленьким пространством событий, и внутри него могут быть другие события, которые вложены в него, и так далее. А, например, вот эту запись "P(H[i])"  можно, исходя из этой логики, записать вот так:

• P(H[i]|O) — потому что данная вероятность считается относительно "O".
  

Теперь разберем формулу полной вероятности на части для того, чтобы понять, что же в ней сокрыто. Довольно сложно сразу понять, что тут творится в этой формуле, но, я думаю, скоро все станет понятно. Начну с того, что перепишу данную формулу немного в ином виде:

• P(A) = (S[0] + ... + S[i] + ... + S[n]) / O   =   S[0]/O + ... + S[i]/O + ... + S[n]/O  =  (S[0]/N[0]) * ( N[0]/O ) + ... + (S[i]/N[i]) * ( N[i]/O ) + ... + (S[n]/N[n]) * ( N[n]/O )
• S[i] — площадь конкретного сегмента пересечения гипотезы H[i]
• N[i]  — площадь всей гипотезы H[i] (включая S[i])
• O  — все исходы или площадь всего эллипса

После небольших преобразований, которые заключались в том, чтобы домножить числитель и знаменатель дробей на величину  "N[i]", мы можем увидеть в ней те вероятности, которые присутствуют в оригинале формулы:

• S[i]/N[i] ----> P(A|H[i])
• N[i]/O ----> P(H[i])

Графически, для более хорошего усвоения, это все можно изобразить вот так:

 

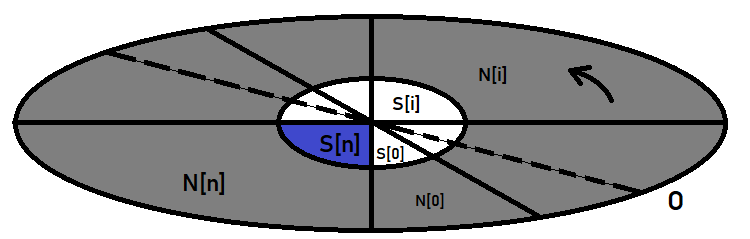
Внешний эллипс здесь исполняет роль пространства событий, а центральный  — роль нашего события, вероятность которого мы ищем. Если представить, что это часы то, проведя диаметр эллипса и вращая его против часовой стрелки, будем нарезать наш эллипс на сегменты, которые и являются гипотезами. Гипотеза  — это просто такое специальное название событиям, но по сути это те же события, которые ничем не отличаются от того, вероятность которого мы ищем.

У этой формулы есть частный случай, который поможет нам с построением схемы Бернулли. Представьте, что центральный эллипс полностью находится внутри одной из таких гипотез. Тогда выходит, что все слагаемые данной суммы, которые имеют отношение к остальным гипотезам, автоматически обнуляются, в связи с тем, что вероятность возникновения события "A" в рамках данных гипотез невозможна или равна нулю, что то же самое, что и приводит к обнулению этих слагаемых. В итоге получается что:

• P(A) = P(H) * P(A|H)
• H  — вероятность именно той гипотезы, внутри которой находится выбранное событие, полностью.

Если пойти дальше, то можно предположить, а что если событие "А" также назвать гипотезой? А почему нет, гипотеза это  — событие, значит любое событие  — гипотеза. Теперь предположим, что есть еще одно событие "B", которое находится уже внутри "A", тогда получается, что "A" является гипотезой по отношению к "B", и к этим двум событиям тогда становится применима предыдущая формула:

• P(B) = P(A) * P(B|A) = P(H) *  P(A|H) *  P(B|A)

Подставив туда вместо  "P(A)" предыдущее соотношение, уже видна некая закономерность построения общей формулы для любого количества вложенных друг в друга гипотез или событий. И зачем нам это, спросите вы? А я отвечу, что это прямой прообраз формулы Бернулли, которую мы разберем чуть ниже, а пока что разберем кое-что очень любопытное.

О фракталах

Если придерживаться логики, которая была выше, то выходит что, если P(A) + P(B) = 1, то это полная группа событий, и выходит, что полная группа может быть собрана из двух произвольных цепочек гипотез, которые вложены друг в друга. Но данные гипотезы могут быть совместными, а если потребовать, что все возможные вложенные друг в друга гипотезы были бы несовместными с гипотезами других цепочек, то тогда это будет автоматически приводить к тому, что все цепочки будут несовместными с другими цепочками в данном пространстве событий. Если внимательно подумать, как это будет выглядеть графически, то получим очень интересное образование:

Данное образование называется "Фракталом", а все потому, что невозможно построить такую структуру до конца, ее можно строить до бесконечности. На моем рисунке она построена всего на 3 уровня вглубь. Синие прямоугольники здесь олицетворяют конец отдельной цепочки вероятностей. Самое интересное то, что если просуммировать вероятности всех этих цепочек, то они будут образовывать полную группу событий.

Для описания таких фракталов, как оказалось, очень хорошо подходят "сочетания". Сочетания строятся на основе такого понятия как "факториал". Существует еще такое понятие, как "перестановка", по иерархии данное понятие лежит между факториалом и сочетанием. Из формулы факториала выводится формула перестановок, а уже из формулы перестановок вытекает такое понятие как сочетание. Я приведу эти формулы:

• n! - факториал числа "n"
• P(n,k) = n! / ( n - k )!  — перестановки из "N" элементов по "К" элементам
• С(n,k) = n! / ( k! * ( n - k )! )  — сочетания из "N" элементов по "К" элементам

Думаю, что ни для кого не секрет, что факториал  — это произведение всех натуральных чисел начиная с "1" и заканчивая числом "n", при этом "0! = 1". То есть факториал нуля равен единице, в данном случае это просто исключение из правил, но на самом деле, я не видел ни одного случая, где данное исключение мешало вычислениям или усложняло бы алгоритмы, скорее наоборот.

Перестановки  — это уже кое что посложнее. Представьте, что у вас есть колода карт и в данной колоде есть какое-то количество карт, и мы придумали простой опыт: мы должны перемешать колоду и вынуть из нее совершенно произвольным образом несколько карт и разложить их на столе в том порядке, в котором мы их вынимали из колоды. Так вот, перестановки это как раз количество всех возможных исходов данного опыта, при этом порядок следования карт тоже считается уникальным идентификатором конкретного исхода. Понятно, что это применимо не только для опытов с картами, а к чему угодно, да хоть к камням или к карандашам.

Первую карту можно вынуть из колоды "n" способами, вторую "n-1" способами, так как той карты, которую вынули первой из колоды, ее уже нет в колоде, и так далее до "n-k-1". Получается, чтобы получить количество всех возможных перестановок, нужно перемножить все эти числа от "n-k-1" до "n". Понятно, что это очень напоминает нам факториал. Если мы возьмем "n!" и разделим его на последние "n-k" множителей, то получим как раз то произведение, которое было изначально, а это произведение в точности равно "(n-k)!". Вот так и получаем знаменитую формулу перестановок.

Формула сочетаний чуть сложнее, но тоже очень легко выводится. Теперь немножко подумаем, если мы набрали все возможные перестановки, но теперь порядок следования ее элементов не имеет для нас никакого значения, а имеет значение только, какие карты выпали в данном наборе. Теперь нам требуется найти количество всех таких случаев, где мы получили немного другой набор карт отличный от всех других. По сути, каждая перестановка уже содержит в себе какой-то один из этих уникальных наборов, но все нам они не нужны. Теперь немного изменим логику размышлений, мы попробуем набрать все перестановки из всех возможных сочетаний: тогда выходит, что если мы берем одно какое-то сочетание, то как бы мы не переставляли элементы в нем, то каждая такая перестановка будет уникальной. Более того, если взять все такие уникальные сочетания и произвести в них все возможные перестановки элементов, то мы как раз и получим все возможные перестановки, и получается что:

• P(n,k) = C(n,k) * P(k,k)

Kоличество всех уникальных перестановок внутри одного сочетания как раз равно "P(k,k)", потому что нам нужно набрать из "k" вариантов все возможные перестановки по этим же "k" вариантам. Отсюда видно, что разделив обе части уравнения на "P(k,k)", мы можем получить ту искомую формулу сочетаний:

• C(n,k) = P(n,k)/P(k,k) = n! / ( k! * ( n - k )! )
  

Как перестановки, так и сочетания, повсеместно используются в различных задачах по теории вероятности, но если говорить о практическом применении в трейдинге, нам будут исключительно полезны именно сочетания. С помощью них как раз строятся фрактальные функции для множества целей. Возможно, более правильно будет их назвать рекуррентными, но я почему-то такие функции называю фрактальными, наверное потому что они действительно фрактальные, в них уже не просто рекурсия, а целое дерево вызовов.

Схема Бернулли

Прежде чем мы начнем рассмотрение таких фрактальных функций, мы должны рассмотреть именно эту знаменитую формулу. Представим, что у нас есть цепочка одинаковых опытов, которую мы должны повторить несколько раз. В результате опыта  с определенной вероятностью должно появиться или не появиться некое событие. Далее предположим, что нам захотелось найти вероятность того, что в цепочке из "n" опытов наше событие появится ровно "k" раз. Формула Бернулли может ответить на этот вопрос:

• P = C(n,k)*Pow(p,k)*Pow(q,n-k)   — формула Бернулли
  
• p  — вероятность выпадения события в результате единичного опыта
• q = 1 - p   — вероятность того, что событие не произойдет в результате опыта

Вспоминая формулу, выведенную нами для вероятностных цепочек, расширим ее для случая сколь угодно большой длины цепи:

• P(n) = P(H[1]|O) *  P(H[2]|H[1]) *  P(H[3]|H[2]) * ... * P(H[k]|H[k-1]) * ... *P(H[n]|H[n-1])
• n  — количество сегментов цепи
• O  — все множество исходов, можно так же обозначить как H[0]

Эта формула считает вероятность того, что произойдет именно та цепочка гипотез, которая нам нужна. Визуально можно эту формулу изобразить так:

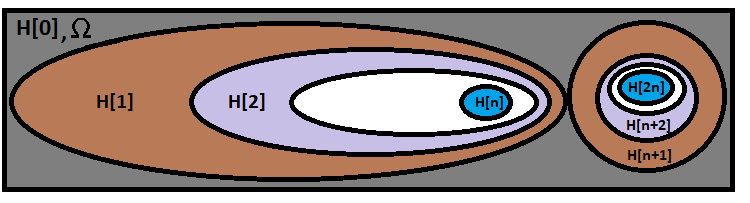
В первом и самом большом эллипсе наша формула, а другая цепочка, которая нарисована рядом, несовместна с нашей цепочкой, она и символизирует какую-то другую ветку из другого сочетания. Таких веток ровно столько, сколько вариантов вычисления сочетаний в нашей формуле. Только не путайте сами сочетания с вариантами вычисления сочетаний. Количество вариантов вычисления сочетаний равно:

• n+1 ( потому что сочетания из "0" успешных исходов тоже считаются )
• n  — количество независимых испытаний в цепочке опытов

А теперь представим, что вероятности всех этих гипотез равны или "p" или "q". Тогда формула упрощается:

• P(n) = Pow(p,k)*Pow(q,n-k)
• k  — сколько множителей равных "p" присутствует в произведении
• n-k  — сколько множителей равных "q" присутствует в произведении

Уже видно сходство с формулой Бернулли, не хватает только сочетания. Но если хорошенько подумать, то станет понятно, что вариантов цепей со схожей вероятностью и количеством "k" и "n-k" как раз в точности равно "C(n,k)". А так как все эти цепочки вероятностей несовместны друг с другом, то выходит, что вероятность того, что мы получим какую-то из данных цепочек, будет равно сумме вероятностей всех таких цепочек. А так как эти вероятности одинаковы, то можно просто умножить вероятность одной цепочки на их количество, вот и получаем нашу формулу Бернулли:

• P = C(n,k)*Pow(p,k)*Pow(q,n-k)

Интересно, что и эту формулу можно расширить, например на те случаи, когда требуется найти вероятность не четко фиксированного сочетания появления, а выпадение события "k" и более раз, "k" и менее раз, а так же все возможные вариации на эту тему. В данном случае будет сумма вероятностей для нужных нам сочетаний. Например, вероятность того, что событие выпадет больше чем "k" раз будет считаться так:

• P = Summ(k+1 ... i ... n)[C(n,i)*Pow(p,i)*Pow(q,n-i)]

Очень важно так же понимать что:

• P = Summ(0 ... i ... n)[C(n,i)*Pow(p,i)*Pow(q,n-i) ] = 1

Иначе говоря, все возможные цепочки и образуют полную группу несовместных событий. А так же очень важным тождеством является:

• Summ(0 ... i ... n)[C(n,i)] = Pow(2,n)
  

Я думаю, это логично, учитывая, что у каждого сегмента вероятностной цепочки всего два состояния  — "событие произошло" и "событие не произошло". Состояние, когда событие не произошло  — это точно такое же событие, просто оно заключается в том, что произошло что-то другое.

Так же у сочетаний есть очень интересное свойство:

• C(n,k) =  C(n,n-k)
  

Прийти к нему можно, посчитав чему равно "C(n,n-k)" и сравнив с "C(n,k)". После небольших преобразований будет видно, что оба выражения идентичны. Я набросал небольшую программку на основе MathCad 15 для того чтобы проверить все вышесказанные утверждения: 

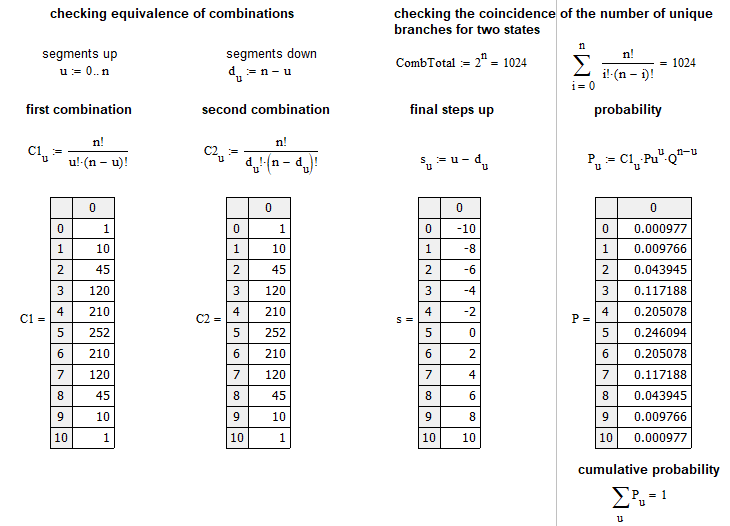
Данный пример я сделал приближенным к рынку, и он вычисляет вероятность того, что из "n" шагов рынок пройдет "u" шагов вверх. Шагом считается движение цены на некоторое количество пунктов вниз или вверх, относительно предыдущего шага. Графически массив вероятностей для каждого "u" можно изобразить вот так:

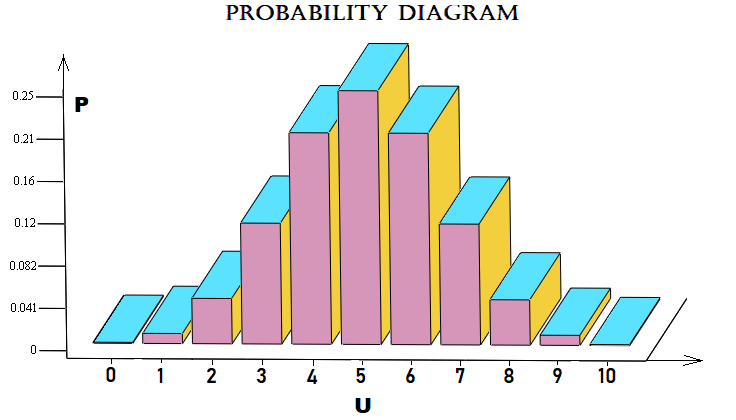
В данном случае для простоты я использовал схему Бернулли с "10" шагами. Файл будет приложен к статье и желающие смогут поиграться с ним. Не обязательно применять эту схему к ценообразованию, она так же применима и к ордерам, и к чему угодно.

Создаем первый фрактал

Отдельной проработки требуют вопросы касающиеся стоп лоссов и тейк профитов сделок. Я думаю, всем интересно, как посчитать вероятность закрытия сделки по стоп лоссу или по тейк профиту, когда известны величины этих стоп лоссов и тейк профитов в пунктах (расстояние от текущей цены). Данную величину можно вычислить в любой точке, даже если это уже не цена открытия, так как это все находится в прямой зависимости от механизмов ценообразования. На данном примере я хочу продемонстрировать доказательство формулы с применением фракталов. В случае случайного блуждания посчитать данную вероятность можно так:

• P(TP) = SL / ( TP + SL ) - вероятность срабатывания тейк-профита
• P(SL) = TP / ( TP + SL ) - вероятность срабатывания стоп-лосса
• SL  — расстояние в пунктах до стоп-лосса
  
• TP  — расстояние в пунктах до тейк профита

Думаю всем понятно, что эти две вероятности образуют полную группу:

• P(TP) + P(SL) = 1
  

Из этой формулы автоматически вытекает, что при случайной торговле математическое ожидание всех таких стратегий будет нулевым, если не учитывать спред, комиссию, своп:

• M =  P(TP) * TP - P(SL) * SL = 0

Это простейший случай, когда мы открываемся фиксированными стопами, но это все при желании можно обобщить на случай абсолютно любой стратегии, а сейчас мы займемся тем, что докажем эту формулу, используя тот же MathCad 15. Я уже давно работаю с этой программой и она позволяет проводить вычисления практически любой сложности, даже с применением программирования. На данном примере мы не только докажем формулы, которые я написал выше, но и увидим первый пример построения фрактальной функции. Начнем с того, что изобразим схематично наш процесс движения цены так, как мы его представляем. Мы не можем здесь использовать непрерывные функции, а лишь дискретные. Для этого условно возьмем наш ордер и отложим наши расстояния (стопы) вверх и вниз, после чего разделим эти сегменты на части с равным шагом, так чтобы в каждом сегменте укладывалось целое количество шагов, и представим, что цена движется по этим шагам. В данном случае очевидно, что так как шаги все одинаковые, то вероятность шага в любом из двух направлений в точности равна "0.5". Для реализации соответствующего фрактала нам потребуется графическая иллюстрация:

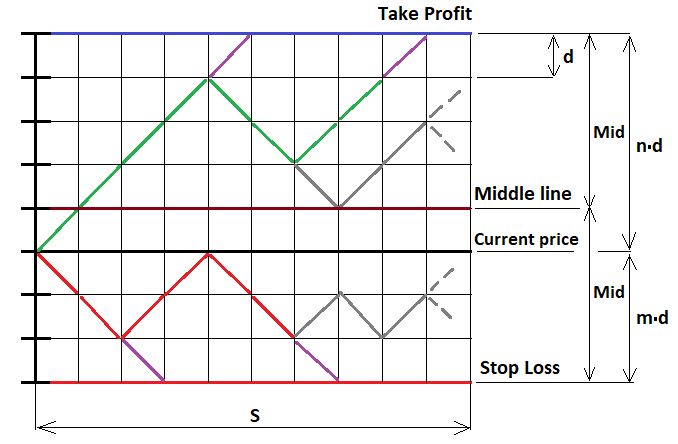
Для того чтобы решить данную задачу, мы должны рассмотреть три возможных случая продолжения фрактала:

1. Мы выше средней линии  ( U > MiddleLine )
2. Мы ниже средней линии  ( U < MiddleLine )
3. Мы сейчас находимся на уровне средней линии ( U = MiddleLine )

В роли "U" здесь выступает итоговое количество шагов "u-d" вверх, относительно цены открытия, если точка, из которой мы собираемся продолжить построение фрактала, находится ниже этой цены, то данная величина принимает отрицательные значения в соответствии с формулой. В случае если мы на средней линии, то количество шагов, которое мы имеем право сделать, не опасаясь пересечения линии, ровно на единицу меньше чем "Mid". Но прежде чем приступать к построению, мы обязательно должны ограничить построение фрактала количеством шагов которое цена или ордера имеют право сделать. Если количество шагов превысит требуемое, то мы обязаны прервать дальнейшее его построение. В противном случае мы получим бесконечную рекурсию, из которой невозможно будет выйти, и время ее вычисления будет равно бесконечности.

На рисунке я нарисовал несколько пурпурных шагов, в этих точках мы собираем вероятности и суммируем в общую переменную, а после этого должны развернуть нашу цепочку вверх или вниз, в зависимости от того, в какую границу уперлась наша цепь, чтобы она могла продолжить движение дальше и построение новых вложенных фрактальных уровней. В остальных точках мы можем свободно строить полные фрактальные уровни на основе схемы Бернулли, которую мы рассмотрели выше.

В случае, когда мы имеем право строить дерево на основе схемы Бернулли, мы должны в первую очередь определить количество шагов, которое мы вправе сделать, учитывая экстремальные случаи, когда все шаги будут исключительно вверх или исключительно вниз. Для всех трех случаев данная величина принимает значения:

• (n - 1) - U  — когда наша цепь уже выше средней линии ( так как увеличение U влечет за собой уменьшение расстояния до верхней границы )
• (m - 1) + U  — когда наша цепь уже ниже средней линии ( так как уменьшение U влечет за собой уменьшение расстояния до нижней границы )
• (floor(Mid)-1)  — когда наша цепь ровно на средней линии
• n  — количество верхних сегментов
• m  — количество нижних сегментов
• floor  — функция отбрасывает дробную часть числа ( возможно это и не нужно пока пусть так )

При этом предварительно нужно посчитать две вспомогательные величины:

• Mid = (m+n)/2  — половина ширины коридора ( в шагах )
• Middle = (m+n)/2 - m   — значение "U" для серединной линии ( в шагах )

Данные величины пригодятся в дальнейшем для описания логики ветвления фрактала. Только фрактал мы будем строить пока что только для случаев "n>=m". Но этих данных пока еще недостаточно для корректного построения фрактала. Для того чтобы иметь возможность построения дальнейших более глубоких уровней фрактала, необходимо переопределять "U" для каждого нового сочетания из схемы Бернулли и передать его в новый фрактальный уровень. Кроме того, необходимо правильно инкрементировать количество произведенных шагов и так же правильно передавать их дальше. Точно так же придется собирать вероятность всей цепочки с помощью множителей очередного фрактального уровня и передавать вероятность промежуточной цепи дальше в следующий уровень, пока этот процесс не завершится успешным пересечением нужной границы. Для лучшего понимания я создал иллюстрацию для всех трех вариантов:

  

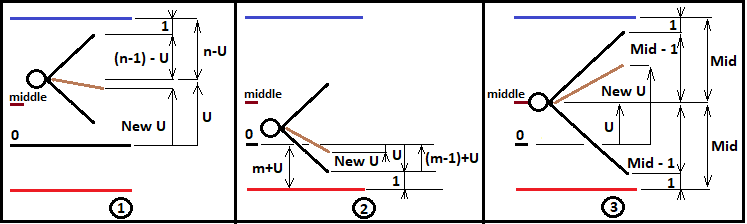
Руководствуясь данной диаграммой, можно теперь написать чему будут равны величины "NewU" и иные вспомогательные величины для каждого случая из всех представленных, мы рассмотрим это на примере построения фрактала для вычисления вероятности пересечения верхней границы:

Для случая 1:

Разберем верхнюю картинку и опишем математически то, что там происходит. На данной картинке выжимка из моей программы в MathCad 15. Я не стал приводить весь листинг, желающие смогут с ним ознакомиться в приложении к статье, но самые важные моменты я вынес, потому что как раз на них и стоит весь фрактал. Еще нужно помнить, что первый прямоугольник находится в цикле и итерируется по "i" для описания всех возможных сочетаний. Данную логику при желании можно повторить в среде разработки MetaEditor. Начнем с первой иллюстрации на диаграмме. Для того чтобы определить "NewU", нам сначала необходимо определить некоторые основополагающие формулы, которые нам помогут в этом:

• ( n - 1 ) - U = f — данная величина в данном случае является количеством шагов будущего дерева сочетаний (размер обусловлен расстоянием до ближайшей границы коридора фрактала)
• u + d = f  — та же самая величина, только выраженная через количество растущих и падающих сегментов
• s = u - d  — количество итоговых шагов вверх, выраженная через падающие и растущие сегменты
• u = i  — потому что у меня в программе итерируется именно по "i" ( просто это надо помнить )

Для того чтобы вычислить все необходимые величины, нам требуется выразить "s" через "U" и "i", займемся этим. Для этого нам просто нужно исключить переменную "d". Сначала выразим ее, после чего подставим в выражение для "s":

1. d = f - u = f - i = ( n - 1 ) - U - i
2. s = i -( n - 1 ) + U + i = -( n - 1 ) + 2*i + U

Далее, используя найденное выражение для "s", найдем "NewU" и все величины, которые нам нужны для передачи в следующий фрактальный уровень:

• NewU = s + U = -( n - 1 ) + 2*i + 2*U   - наше новое "U" для передачи в следующий фрактальный уровень
• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) = P * C( ( n - 1 ) - U ,i) * Pow(p,i) * Pow(1-p,( n - 1 ) - U -i)  — наша новая вероятность цепочки "P" для передачи в следующий фрактальный уровень (получаем домножением на вероятность нового сегмента цепи) 
• NewS = S + f = S + ( n - 1 ) - U  — наше новое "S" для передачи в следующий фрактальный уровень

Теперь рассмотрим нижний прямоугольник. В нем мы обрабатываем случаи, когда цепочка шагов дошла до верхней границы коридора. Нам нужно обработать здесь два случая:

1. Сбор вероятности цепочки которая пересекается с границей ( данное действие подчеркнуто красным )
2. Аналогичные действия по инкременту новых значений которые мы передадим в следующий фрактальный уровень

Данный случай очень прост, потому что возможно всего два случая:

1. Касание границы
2. Разворот от границы

На каждое из этих действий не понадобится схема Бернулли, ведь в данном случае происходит всего по одному шагу. Кстати, вероятность разворота домножается именно на "(1-p)", потому что вероятность пересечения "p", а эти два события должны образовывать полную группу, как нам уже должно быть понятно из предыдущих выкладок. Естественно, шаги мы инкрементируем на "1", а "U" уменьшаем на "1", потому что отражение вниз, и нужно эту величину уменьшать. Вот и все что нам понадобится для правильного построения данного случая. Эти правила будут практически идентичны для построения основных фракталов, которые нам понадобятся для совершенно разных целей.

Для случая 2:

Для данного случая вычисление происходит практически идентично, разница только в том, что "f" уже принимает другое значение:

• ( m - 1 ) + U = f

Точно так же выразим "s" через "U" и "i", используя те же формулы, что в предыдущем случае:

1. d = f - u = f - i = ( m - 1 ) + U - i
2. s = i -( m - 1 ) - U + i = -( m - 1 ) + 2*i - U

Точно так же находим все величины, которые нам нужны для передачи в следующий фрактальный уровень:

• NewU = s + U = -( m - 1 ) + 2*i  - наше новое "U" для передачи в следующий фрактальный уровень
• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) = P * C( ( m - 1 ) + U ,i) * Pow(p,i) * Pow(1-p,( m - 1 ) + U -i)  — наша новая вероятность цепочки "P" для передачи в следующий фрактальный уровень
• NewS = S + f = S + ( m - 1 ) + U  — наше новое "S" для передачи в следующий фрактальный уровень

Нижний прямоугольник тут практически идентичен предыдущему случаю, за исключением того, что "U" мы увеличиваем на единицу, так как отражение идет вверх, и это означает увеличение "U". Стоит еще отметить, что в данном случае не происходит сбора вероятностей, потому что в данном фрактале нас не интересуют случаи пересечения с нижней границей. Осталось только разобрать самый последний случай, когда цепь попала на среднюю линию коридора.

Для случая 3:

Определим "f":

• floor(Mid) - 1 = f

Найдем "s":

1. d = f - i =  floor(Mid) - 1 - i
2. s = i - d = -(floor(Mid) - 1) + 2*i

Наконец, найдем величины для передачи в следующий фрактальный уровень:

• NewU = s + U = -(floor(Mid) - 1) + 2*i + U
  
• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) = P * C( floor(Mid) - 1 ,i) * Pow(p,i) * Pow(1-p,floor(Mid) - 1 - i)  — наша новая вероятность цепочки "P" для передачи в следующий фрактальный уровень
• NewS = S + f = S + (floor(Mid) - 1) — наше новое "S" для передачи в следующий фрактальный уровень

Отличительной особенностью данного случая является то, что в данном блоке не происходит сбора вероятностей, потому что данный сбор возможен только на приграничных значениях "U", где также происходит отражение вероятностных цепочек обратно внутрь коридора для того, чтобы они имели возможность распространяться дальше. Построение фрактала для вычисления вероятности пересечения с верхней границей будет идентично, за тем лишь отличием, что сбор вероятностей будет происходить не в первом случае, а во втором.

Интересной особенностью построения подобных фракталов является обязательное наличие в таких функциях формулы Бернулли. Сочетания выделены розовым, а произведения вероятностей желтым. Вместе эти два множителя как раз и образуют формулу Бернулли.

Теперь мы одновременно проверим как правильность построения всего фрактала, так и предположение о том, что математическое ожидание прибыли зависит только от предсказательной способности. Шаги можно представлять как пункты и как сделки, в последнем случае пункты просто нужно будет умножить на соответствующий коэффициент пропорциональности, который зависит от лотов и размера тика, но в данном случае мы посмотрим, как это будет выглядеть для пунктов, потому что такое представление является универсальным:

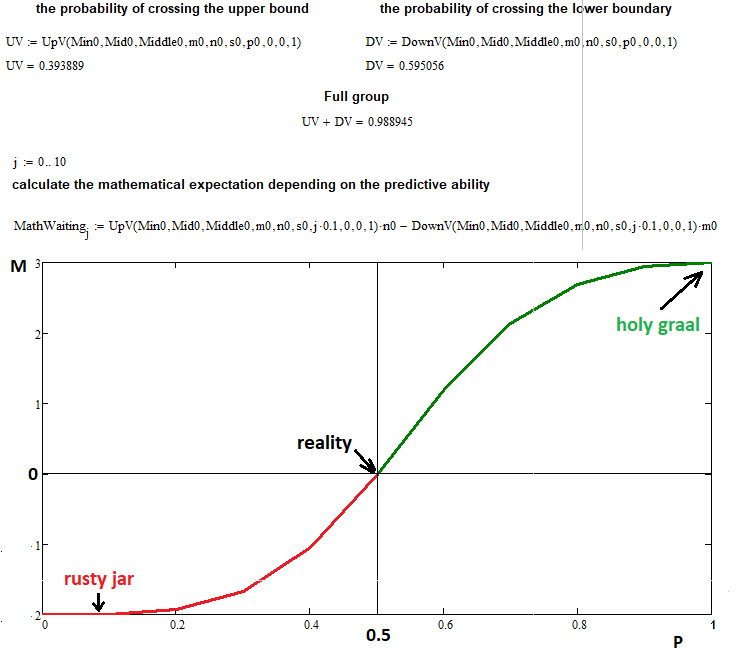
В данном примере я взял следующие входные данные для построения графика зависимости математического ожидания от вероятности шага вверх:

• n = 3 — количество верхних сегментов
• m = 2  — количество нижних сегментов
• s = 22  — количество допустимых шагов для цепной реакции фрактальной функции ( если его увеличивать компьютеру становится очень тяжело, но и этого количества шагов хватает для достаточной точности )
• 0 ... 0.1 ... 0.2 ...... 1.0   — разделил диапазон вероятностей шага вверх на "10" частей с шагом равным "0.1"

Как видно, при вероятности равной "0.5" математическое ожидание наших сделок в точности равно нулю, как и было предсказано формулой, которую мы доказывали с помощью данного фрактала. В экстремальных точках "0" и "1" можно увидеть, что значение функции стремится к "n" и "-m", что полностью согласуется с нашими предположениями. Фрактал успешно выполнил свою задачу, хоть и обнаружился вполне предсказуемый недостаток: лавинообразное возрастание сложности и времени вычисления. Если возникнет потребность, я думаю подождать час-другой, да даже сутки не так уж и сложно, учитывая, что это единственный способ решения многих задач.

Хочется еще сказать, что данный фрактал будет работать только для случаев когда "n >= m", иными словами, когда удаление верхней границы от точки старта больше, чем удаление нижней границы, но нам вовсе не нужно во фрактале предусматривать подобные вещи. Данная конструкция зеркальна в том плане, что если  вдруг  "n < m", то мы можем просто вычислить этот фрактал передав в него "m" вместо "n" и "n" вместо "m", и после этого так же поменять вероятности местами и получим простое перетусовывание двух значений, все это делается очень легко. Подобные фракталы могут быть использованы не только для доказательства каких-то формул, а также для обратного процесса. Некоторые формулы могут быть получены только как результат применения фракталов.

Выводы

Если внимательно изучить данный материал, то я считаю, что в нем были сделаны следующие очень важные умозаключения:

• Теория вероятностей в тандеме с программированием может дать нам теоретическую базу для описания многих процессов на рынке.
• Доказано что фракталы в тандеме с основными положениями теории вероятностей могут дать ответы на самые сложные вопросы.
• Полностью разобран пример построения довольно сложного фрактала.
• Вся теория была проверена на практике с использованием программирования в среде MathCad 15.
• Доказано, что схема Бернулли дает возможности для построения любых фракталов с двумя состояниями шага.

Заключение

Я надеюсь, читатель из данного материала смог увидеть для себя что-то новое и полезное для практического применения в трейдинге. Занимаясь разработкой этой статьи, я старался передать всю мощь дискретной математики и теории вероятностей, для того чтобы подготовить вас к такому непростому занятию, как описание рыночных процессов используя фрактально-вероятностные цепочки. Я старался соединить все основные положения теории вероятностей в монолит, который поможет нам в решении самых сложных задач для практического применения в трейдинге, также старался отбросить то лишнее, что может внести неразбериху в наши мозги. В следующей статье вы увидите новые примеры практического применения фракталов и ответы на другие не менее важные вопросы.