Нестационарные процессы и ложная регрессия

Содержание:

• Введение
• Исследование проблемы нестационарности в регрессионном анализе
• Проверка статистических гипотез о параметрах модели регрессии
• Неправильная спецификация регрессионной модели
• Заключение

Введение

Регрессионный анализ, как один из разделов прикладной математической статистики, является одним из самых распространенных методов обработки эмпирических данных при изучении зависимостей между случайными величинами. В то время как корреляционный анализ позволяет выяснить связаны ли две случайные величины между собой, регрессионный анализ дает представление о том, какой формы может быть эта связь. В регрессионном анализе различают парную и множественную регрессию. В данном исследовании для простоты изложения я буду использовать хорошо всем известную модель парной линейной регрессии:

                                                Yt = b0 + b1Xt + et                                 (1)

• Yt - зависимая переменная (отклик);
• Xt - независимая переменная (или объясняющая переменная);
• b0, b1 параметры модели; t - время (0,1,2,...n) n - количество наблюдаемых данных;
• et - случайная компонента, как правило, гауссовский белый шум.

Здесь индекс t указан для того, чтобы подчеркнуть тот факт, что мы имеем дело с временным рядом, что для нас важна последовательность в которой расположены случайные величины.

Задача регрессионного анализа состоит:

• в оценке параметров выбранной модели регрессии (в линейном случае с помощью обычного метода наименьших квадратов)
• проверке статистических гипотез о параметрах модели
• построении доверительных интервалов для полученных оценок параметров

Если в ходе анализа модель признается статистически значимой, тогда считается, что ее можно использовать для прогноза зависимой переменной. Но при применении регрессионного анализа, особенно к анализу временных рядов, всегда нужно помнить об ограничении которое связано с требованием стационарности налагаемым на исследуемые случайные последовательности. Требование стационарности предполагает неизменность функции распределения случайной величины с течением времени и, следовательно, неизменность математического ожидания и дисперсии этой случайной величины. Попытки применить регрессионный анализ к нестационарным процессам могут привести к ложным выводам о наличии значимой взаимосвязи между исследуемыми величинами. В этом случае стандартные статистические тесты такие как F-статистика, t-статистика перестают работать и риск принять ложную зависимость за истинную многократно возрастает.

Исследование проблемы нестационарности в регрессионном анализе

В данной статье я хочу показать с помощью моделирования по методу Монте-Карло как возникает ложная регрессия, если нарушена предпосылка стационарности, а так же если допущена неправильная спецификация модели регрессии в стационарном случае. Для этого я воспользуюсь стандартной библиотекой MQL5, а именно "Статистической библиотекой" для генерирования случайных чисел и расчета критических значений нормального распределения и распределения Стьюдента, а также  графической библиотекой Научные графики для отрисовки полученных результатов. Для расчета параметров регрессионной модели очень удобно воспользоваться методами матричной алгебры, с их помощью все расчеты значительно упрощаются. Например, формула для нахождения параметров регрессионной модели по методу наименьших квадратов в матричном виде записывается как:

(2) 

• X матрица значений независимых переменных;
• Y - вектор-столбец зависимой переменной;
• b - вектор-столбец неизвестных параметров, которые следует оценить по выборке.

В MQL5  вектор b (в нашем случае парной линейной регрессии он будет состоять из двух элементов - b0 и b1) можно найти вычислив псевдообратную матрицу PInv() от матрицы X и умножив ее на вектор Y:

pinv = x.PInv(); 
Coeff = pinv.MatMul(Y);  // вектор параметров линейной регрессии по МНК

Это сокращенный вариант расчета. Можно считать пошагово как указано в формуле:

xt = x.Transpose();
xtm = xt.MatMul(x);
inv = xtm.Inv();      
invt = inv.MatMul(xt);
Coeff_B = invt.MatMul(Y); // вектор параметров регрессии по МНК

Результат будет один и тот же.

Для целей моделирования нам понадобится модель случайного блуждания как пример нестационарного процесса. Мы построим эту модель как для зависимой переменной Y так и для независимой переменной X. После чего построим регрессию Y на X и оценим такой показатель как R-квадрат(коэффициент детерминации), посчитаем t-статистику и проанализируем остатки регрессионной модели на корреляционную зависимость.                                            

 Yt = Yt-1 + zt                           (3)

  Xt = Xt-1 + vt                           (4)

zt и vt  - два независимо сгенерированных процесса гауссовского "белого шума" c нулевым математическим ожиданием и единичной дисперсией N(0,1);

Две возможные траектории такого процесса изображены на рис. (1)

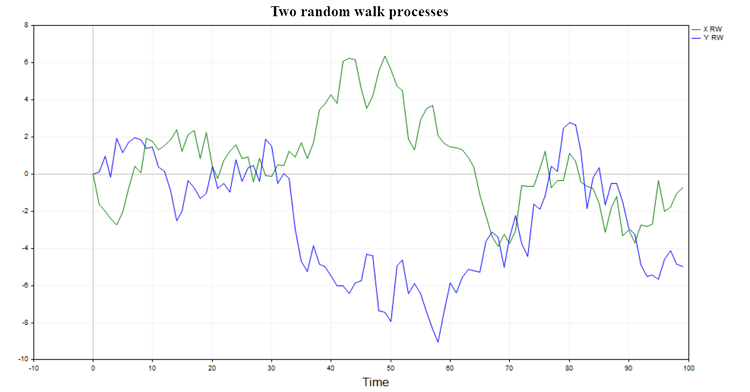
Рис.1.  Два процесса случайного блуждания

У таких процессов нет памяти и они никак не связаны между собой, поэтому естественно ожидать что регрессия одного случайного блуждания на другое не должна давать значимых результатов и гипотеза о наличии связи между двумя случайными блужданиями будет, как правило, отвергаться(за исключением небольшого процента случаев обусловленных выбранным уровнем значимости).

Пример одной из возможных регрессий показан на рис.(2):

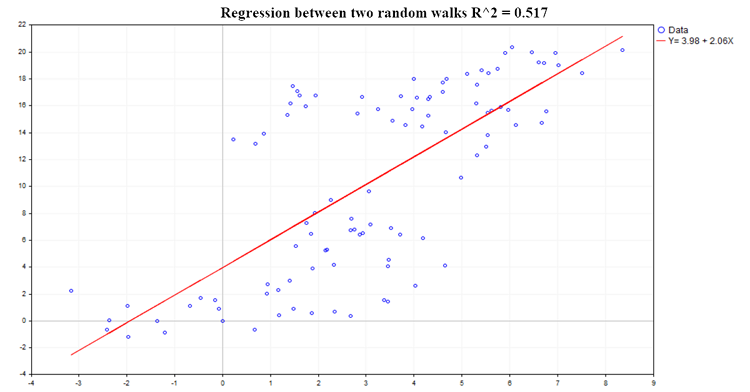
Рис.2. Регрессия между двумя случайными блужданиями, R2=0.517

Такая характеристика исследуемой регрессионной зависимости как коэффициент детерминации (R^2) рассчитывается по формуле: 

R^2 = 1 - SSE/TSS                              (5)

• SSE - сумма квадратов остатков (Sum of squared estimate of errors);
• RSS - объясненная сумма квадратов (Sum of squares due to regression);
• TSS - полная сумма квадратов (Total Sum of Squares =  RSS+SSE);

Код для расчета всех основных характеристик регрессии:

      pinv = x.PInv();
      Coeff = pinv.MatMul(Y);  // вектор параметров линейной регрессии по МНК
      yRegression = x.MatMul(Coeff);  // регрессия y
      res = Y-yRegression;   //  остатки регрессии, y - регрессия y
      yMean = Y.Mean();
      reg_yMean = yRegression-yMean;  // регрессия y - среднее y
      reg_yMeanT = reg_yMean.Transpose();
      RSS = reg_yMeanT.MatMul(reg_yMean);  // Сумма( регрессия y - y среднее )^2 , Объясненная сумма квадратов
      resT = res.Transpose();
      SSE = resT.MatMul(res);  // Сумма(y - регрессия y)^2
      TSS = RSS[0,0]+SSE[0,0];  // Общая сумма квадратов
      RSquare = 1-SSE[0,0]/TSS;  // Коэффициент детерминации R-квадрат
      R2_data[s] = RSquare;

      Vres = SSE[0,0]/(T-2);           // оценка дисперсии остатков
      SEb1 = MathSqrt(Vres/SX);        // оценка стандартного отклонения коэффициента b1 регрессии Y = b0 + b1*X;
      t_stat[s] = (Coeff[1,0]-0)/SEb1; // находим t-статистику для коэффициента b1 при гипотезе, что b1 = 0;

Значения R^2 лежат в диапазоне от 0 до 1. В случае парной линейной регрессии R^2 равен квадрату обычного коэффициента корреляции между X и Y. Когда X не влияет на Y, тогда R^2 близок нулю, а когда зависимая переменная Y объясняется зависимой переменной X то R^2 стремиться к единице. В нашем случае регрессии двух независимых случайных блужданий логично было бы ожидать, что он будет распределен около нуля.  Для того, что бы это проверить, построим распределение R^2 смоделировав методом Монте-Карло 1000 пар случайных блужданий по 100 наблюдений в каждом, с последующим расчетом коэффициента R^2 для каждой пары. В итоге получим следующее распределение рис.(3):

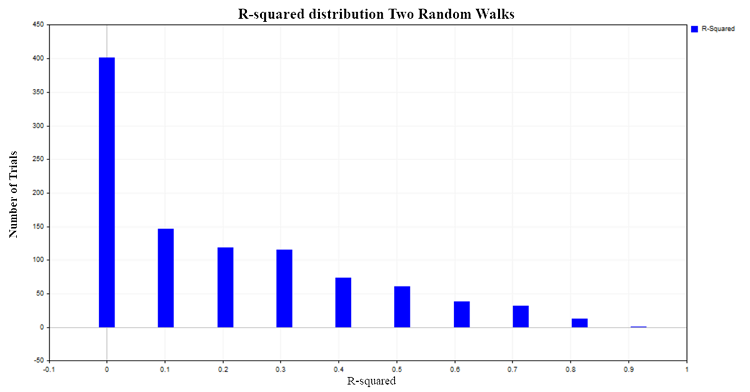
Рис.3.  Распределение R2 для двух случайных блужданий

Приблизительно в 50% случаев коэффициент детерминации демонстрирует значения больше  0.2 указывая на наличие связи между величинами, которые на самом деле никак между собой не связаны. Для сравнения получим распределение R^2  для двух независимых, но уже стационарных процессов. В качестве такого процесса подойдет модель гауссовского белого шума.

                    Yt =  et                                   (6) 

 et  -  гауссовский  белый шум N(0,1)

Сгенерируем 1000 пар стационарных случайных процессов по 100 наблюдений в каждом. В итоге получим вполне ожидаемое распределение R^2 около нуля рис.(4):

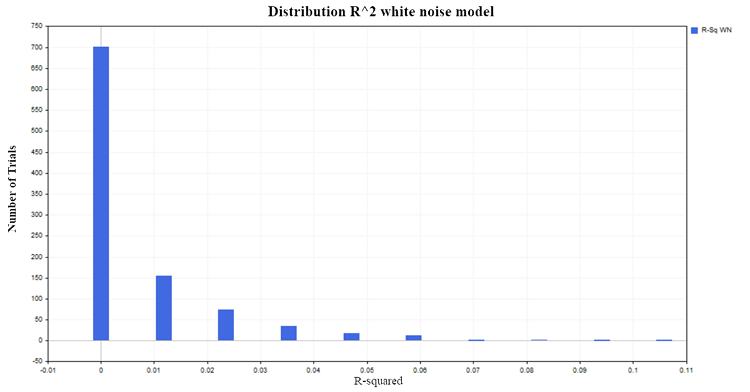
Рис.4. Распределение R2, модель белого шума

Вернемся к случаю двух случайных блужданий и посмотрим теперь как себя ведет  t-статистика, которая рассчитывается для оценки значимости параметров в нашей модели линейной регрессии.

Проверка статистических гипотез о параметрах модели регрессии

Коэффициенты регрессии вычисленные по выборке, сами являются случайными величинами и поэтому возникает необходимость проверки значимости этих выборочных характеристик. При проверке значимости параметра регрессии b1 выдвигается нулевая гипотеза(H0) о том, что объясняющая переменная X  не  влияет на зависимую переменную Y.  То есть H0(i) : b1 = 0 и параметр b1 не значимо отличается от нуля. Альтернативная гипотеза(H1) утверждает, что параметр b1 значимо отличается от нуля. То есть H1(i) :b1 ≠ 0 и тем самым предиктор X  оказывает влияние на зависимую переменную Y.

Для проверки данной гипотезы используется t-статистика:

                                               t = bi /SEi                                      (7)

SEi - стандартное отклонение оцениваемого параметра bi 

Эта статистика имеет распределение Стьюдента ta/2 (n-p)  с (n-p) степенями свободы.

• n - количество данных используемых для расчета в модели регрессии (в нашем случае 100);
• p - количество оцениваемых параметров (в нашем случае парной регрессии их 2);
• a - уровень значимости (1,5,10%).

Для нашего эксперимента я выбрал 5% уровень значимости. Тогда если значения t-статистики по модулю превысят критическое значения распределения Стьюдента {|t| > t0,025 (98) =1,9844}, то можно сделать вывод об отличии от нуля параметра регрессии b1 и как следствие о наличии связи между объясняющей переменной X и зависимой переменной Y. Так как я выбрал 5% уровень значимости, то мы должны ожидать только приблизительно 5% ложных отклонений нулевой гипотезы от общего количества проведенных испытаний. Но по результатам моделирования t-статистика отклоняет нулевую гипотезу слишком часто (ложно, ведь зависимости нет), приблизительно в 75% случаев, рис (5):

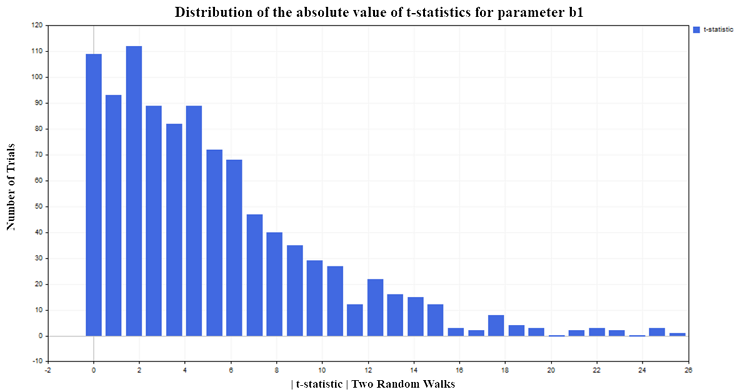
Рис.5. Распределение абсолютного значения t-статистики для параметра b1

Также хочется отметить следующую тенденцию. Чем больше наблюдений в выборке, тем больше становится процент отклонения нулевой гипотезы. Возникает на первый взгляд парадоксальная ситуация, что чем больше выборка, тем больше предиктор X влияет на независимую переменную Y и тем сильнее связь между переменными. На самом деле конечно же никакого парадокса здесь нет, а есть просто приложение регрессионного анализа к тем процессам, к которым он не применим. Видно, что стандартная t-статистика терпит неудачу, когда регрессия применяется к анализу нестационарных временных рядов. Такая ситуация называется ложной регрессией.

Неправильная спецификация регрессионной модели

Но нестационарность — это только одна из причин почему стандартные статистические критерии перестают работать. Они могут вводить в заблуждение даже если два ряда являются стационарными, но при этом нарушена спецификация модели регрессии. То есть если выбрана неверная форма функциональной зависимости между переменными (линейная вместо нелинейной). Или если в модели пропущена независимая переменная X, от которой действительно зависит переменная Y, а вместо нее ошибочно используется абсолютно не значимая переменная. Что бы пояснить это построим два независимых стационарных процесса X и Y. В качестве примера я буду использовать модель авторегрессии первого порядка AR(1):

Yt = A*Yt-1 + zt                           (8)

 Xt = B*Xt-1 + vt                          (9)

• zt и vt   два независимо сгенерированных процесса гауссовского "белого шума" с нулевым математическим ожиданием и единичной дисперсией N(0,1);
• A и B параметры модели AR(1) которые должны быть строго меньше 1 по модулю для соблюдения условия стационарности.

Опять построим регрессию Y на X (для примера, с параметрами AR(1)  A=0.5, B=0.5) при тех же условиях, как и для модели двух случайных блужданий(100 данных в каждом процессе, количество испытаний 1000). В итоге получим следующее распределение t-статистики для параметра регрессии b1 рис(6):

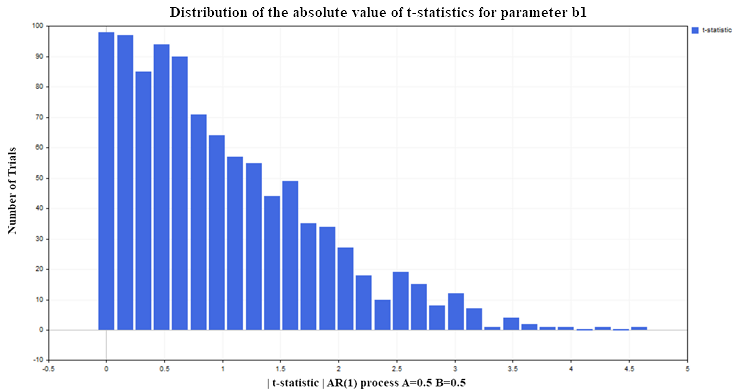
Рис. 6. Распределение абсолютного значения t-статистики для параметра b1

Как видим, здесь ситуация с отклонением нулевой гипотезы обстоит гораздо лучше, чем в нестационарном случае. Всего около 12-13%  ложных отклонений при допустимом уровне в 5%(напомню, что критическое значение распределения Стьюдента для 98 степеней свободы = 1.9844)  Для стационарных процессов этот процент не растет с увеличением объема выборки, а остается на том же уровне. На этот раз t-статистика дает сбой не потому, что переменные нестационарны, с этим как раз все хорошо, а из-за неверной спецификации модели регрессии.  Хотя форма зависимости была выбрана верной(линейная), но мы предположили, что переменная Y зависит не от лаговых значений этой же переменной, а от значений переменной X, которая никакого отношения к переменной Y не имеет. Если мы оставим в модели регрессии переменную X и добавим к ней лаговые значения Y тогда статистические свойства параметров регрессии улучшатся и t-statistica перестанет давать ложные выводы чаще чем установленный уровень значимости (5% в нашем случае). На практике, для того чтобы понять, что модель регрессии ложная или специфицирована не верно, нужно обратиться к анализу остатков 

                                         Residuals =  Yt - Yreg_t                       (10)

• Yt - фактические значения зависимой переменной Y;
• Yreg_t  - расчетные значения регрессии

Если в остатках модели присутствует значимая автокорреляция это является сигналом к тому, чтобы считать данную модель регрессии неправильно специфицированной или ложной. 

Код расчета автокорреляционной функции (ACF) и 99% доверительных интервалов

////////////////////////// расчет ACF /////////////////////////////////////////

   avgres = res.Mean();  // среднее остатков
   ArrayResize(acov,K);
   ArrayResize(acf,K);
   ArrayResize(se,K);
   ArrayResize(se2,K);

   for(i=0; i<K; i++)
     {
      ArrayResize(c,T-i);
      for(j=0; j<T-i; j++)
        {
         c[j] = (res[j,0]-avgres)*(res[j+i,0]-avgres);
        }
      acov[i] = double(MathSum(c)/T);  // Автоковариация
      acf [i] = acov [i]/acov [0];  // Автокорреляция
      se[i] =   MathQuantileNormal(0.995,0,1,err)/MathSqrt(T);    // 99% доверительные интервалы для АКФ //
      se2[i] = -MathQuantileNormal(0.995,0,1,err)/MathSqrt(T);
     }

На рис. (7) показан график автокорреляционной функции (АСF) остатков регрессии для модели двух случайных блужданий.  Так же указаны границы 99% доверительной области для ACF  рассчитанные по формуле  SE = MathQuantileNormal(0.995,0,1,err)/MathSqrt(T); T - количество наблюдений в модели регрессии.

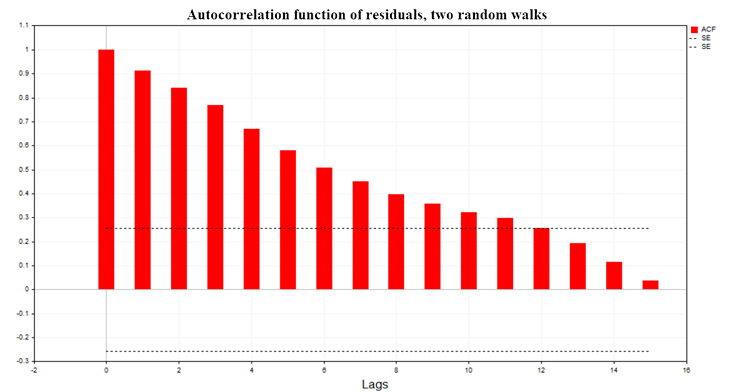
Рис. 7. Автокорреляционная функция остатков, два случаных блуждания

На рис. (8) показан график ACF остатков регрессии для модели двух AR(1) процессов с параметрами (А=0.5, В=0.5)

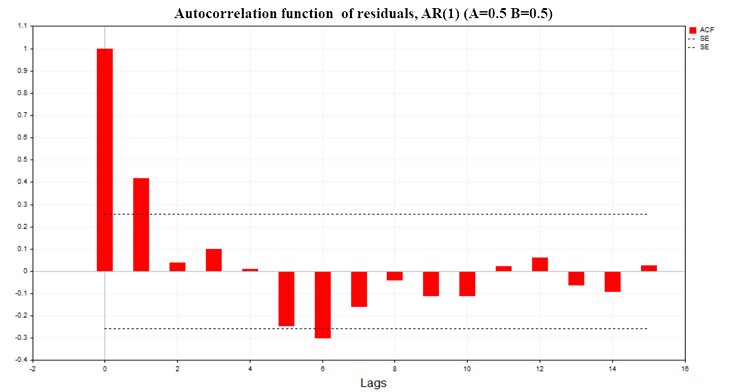
Рис. 8. Автокорреляционная функция остатков, AR(1)  A=0.5  B=0.5

Как видно из графиков, в остатках регрессионных моделей присутствует значимая автокорреляция, следовательно, мы имеем дело с неправильно определенной моделью регрессии или вообще с ложной регрессией. На основе автокорреляционной функции остатков построен также критерий Дарбина-Уотсона (DW-критерий). Он используется для тестирования автокорреляции остатков регрессионной модели  с лагом равным 1. 

                                            DW = 2*(1-ACF(1))                         (11)

При ложной регрессии эта статистика находится около нуля.

Заключение

Основная проблема, которую я хотел затронуть в этой статье заключается в осознании границ применимости статистических методов, в частности методов регрессионного анализа. А также демонстрации тех последствий когда эти границы нарушаются. Очень просто формально провести расчеты, увидеть "значимую" статистику и сделать ошибочный вывод о наличии связи между двумя случайными процессами.

Вывод, который можно сделать из всего вышеизложенного: 

• Перед тем как строить модель регрессии необходимо прежде всего протестировать на стационарность все переменные в этой модели.
• Если какая-то переменная нестационарна, ее нужно привести к стационарному виду (как правило, с помощью взятия первых разностей) и уже дальше пытаться строить модель с этой модифицированной переменной.
• После построения модели нужно обязательно исследовать остатки на автокорреляционную зависимость.
• Если значения автокорреляционной функции остатков не выходят за границы 99% доверительной области, тогда можно переходить к оценке значимости параметров регрессионной модели используя t-статистику.
• Если она окажется значимой, тогда уже можно приступать к прогнозированию зависимой переменной Y по построенной модели.

Для воспроизведения всех вышеизложенных результатов в начале скрипта выбирайте значения переменной M = 1, 0 или 0.5, в зависимости от того, результаты по какой модели вы хотите получить. После чего в самом низу скрипта нужно раскомментировать тот блок кода, который отвечает за отображение той или иной статистики для каждой конкретной модели. Так же во включаемом файле Math.mqh нужно закомментировать две строчки кода для функции которая рассчитывает эмпирическую функцию плотности вероятности (MathProbabilityDensityEmpirical) для отображения частот на графике

 5432  //  for(int i=0; i<count; i++)
 5433 //    pdf[i]*=coef;