母集団最適化アルゴリズム：スマート頭足類（SC、Smart Cephalopod）を使用した変化する形状、確率分布の変化とテスト

内容

1.はじめに
2. 分布確認用テストベンチ
3.必要な分布法則を持つ乱数の構築
4.最適化アルゴリズムテンプレート： スマート頭足類（SC、Smart Cephalopod）アルゴリズム
5.終わりに

1.はじめに

確率論は、無作為な現象を研究し、その発生の可能性を決定する数学理論です。無作為な過程を記述し、分析することができます。確率論の基本概念は、確率、確率変数、確率分布、数学的期待値、分散です。

確率とは、ある事象が発生する可能性を示す数値特性です。

確率変数とは、無作為な実験の各結果を特定の数値に関連付ける関数です。

確率分布とは、確率変数の可能な値のそれぞれの尤度を決定する関数です。

数学的期待値とは、実験を何度も繰り返すことによって得られる確率変数の平均値のことです。

分散とは、数学的期待値に対する確率変数の値の分布の尺度です。

モーメントは、確率変数の分布を表す数値特性です。モーメントは、分布の中心（期待値）とその広がり（分散と標準偏差）を決定し、分布の形状（歪度と尖度）を分析するために使用されます。1次のモーメント(n=1)は数学的期待値であり、確率変数分布の中心を決定します。2次のモーメント（n=2）は分散で、その数学的期待値に対する確率変数の広がりを記述します。3次のモーメント（n=3）は分布の歪度（ひずみ度）の尺度であり、4次のモーメント（n=4）は分布の尖度（凸度）の尺度です。

確率分布は、無作為な現象のモデル化やデータ分析、パラメータの推定や仮説の検定などの統計学において重要な役割を果たしています。これにより、確率変数や事象の確率的特性を記述したり、さまざまな結果の確率を決定したりすることが可能になります。

確率論と最適化は、経済学、金融学、工学、生物学、医学など、科学技術のさまざまな分野で広く使用されている2つの重要な科学分野です。これらの分野の発展とその研究・最適化手法の応用により、複雑な問題の解決や新技術の創造が可能となり、量子コンピューター、安全な超高速通信、生成ニューラルネットワーク、人工知能の創造に向けた最新技術の開発など、さまざまな分野で仕事の効率と質が向上しています。 

確率論に基づく確率計算は、無作為な現象のモデル化やデータ分析において重要な役割を果たしています。最適化とは、様々な問題において最適解を見つけることを目的とし、多くの可能性のある選択肢の中から最適解を見つけることを可能にします。しかし、現実の問題には不確実性や無作為性がつきものです。ここが確率分布の出番です。確率分布によって、最適化問題における無作為性や不確実性を考慮することができます。

確率分布は、進化的アルゴリズムや集団アルゴリズムにも積極的に利用されています。これらのアルゴリズムでは、探索空間における新しい状態の無作為な生成は、適切な確率分布を使ってモデル化されます。これにより、パラメータ空間を探索し、母集団の無作為性と多様性を考慮した最適解を見つけることができます。

より洗練された最適化手法は、確率分布を使って不確実性をモデル化し、複雑な関数を近似します。これにより、パラメータ空間を効率的に探索し、データの無作為性やノイズを考慮した最適解を見つけることができます。

この記事では、さまざまな種類の確率分布とその特性、そしてコードに対応する関数の形式での実用的な実装について見ていきます。様々なタイプの分布で乱数を生成する場合、無限の尾の長さや分散境界を設定する際の確率のずれなど、多くの問題に遭遇する可能性があります。最適化アルゴリズムを設計・作成する際には、しばしば数学的な期待値に対して確率をシフトさせる必要があります。この記事の目的は、このような問題を解決し、確率を扱うための作業関数を作成し、その後の最適化アルゴリズムで使用することです。

2.分布確認用テストベンチ

確率変数の分布をテストし可視化するには、分布の形状を明確に表示できるテストベンチが必要です。これは最適化アルゴリズムを設計する際に重要なことで、確率変数の確率をどの方向にシフトさせるかを視覚的に表現し理解することは、最良の結果を達成するのに役立つからです。

確率分布を作るには、乱数が入る一連の箱のようなものを作る必要があります。箱は基本的にカウンタです。例えば、左側がmin、右側がmaxで囲まれ、その間にinが横たわる数直線はこのように想像できます。

min|-----|-----|-----|-----|-----|-----|in|--|--|--|--|--|--|max

inの値がmax寄りにシフトしていることがわかります。[min;max]の範囲で乱数を発生させると、[in;max]の範囲よりも[min;in]の範囲の乱数の方が多くなるため、数字が落ちる確率が左にずれてアンバランスになりますが、左右の落下数が平均して同じになるように、確率をずらさずに分布の形を変える必要があります。そのためには、左右の箱の数を同じにする必要があります（上図の例では、左右に6つの箱がある）。

つまり、分布を構築するためのテストベンチは非常にシンプルなのです。その仕事の本質は次のようなものです。

• キャンバスを操作するためのCCanvasオブジェクトを作成する
• 設定で選択された分布で乱数を生成する
• 乱数が該当する箱のどのエリアにあるかを確認し、その箱に1を加える
  
• すべての箱に入った数の最小値と最大値を数える
• 箱ごとの乱数量に対応する円をキャンバスに描く
• 青（めったにない）から赤（よくある）までの色で円を塗る
  

このコードの全体的な目標は、グラフを使って確率分布をキャンバス上に視覚化することです。それぞれの円は、すべての箱の最小/最大数で正規化された、箱に描かれた乱数の量です。

#property script_show_inputs
#include <Canvas\Canvas.mqh>

enum E_Distribution
{
  uniform = 0,
  gauss   = 1,
  power   = 2,
  levi    = 3
};

//--- input parameters
input double         MinP       = -100.0;
input double         InpP       =  0;
input double         MaxP       =  100.0;
input int            CNT        =  1000000;
input int            Size       =  1000;
input double         SigmaP     =  3;       //Sigma for "Gauss" distribution
input double         PowerP     =  2;       //Power for "Power law" distribution
input double         LeviPowerP =  2;       //Power for "Levy flights" distribution
input E_Distribution Distr_P    = gauss;    //Distribution type

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  CCanvas Canvas;

  int W = 750;
  int H = 400;
  int O = 10;

  int CountL [];
  int CountR [];

  ArrayResize     (CountL, Size);
  ArrayInitialize (CountL, 0);

  ArrayResize     (CountR, Size);
  ArrayInitialize (CountR, 0);

  string canvasName = "Test_Probability_Distribution_Canvas";
  if (!Canvas.CreateBitmapLabel (canvasName, 5, 30, W, H, COLOR_FORMAT_ARGB_RAW))
  {
    Print ("Error creating Canvas: ", GetLastError ());
    return;
  }

  ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN,     false);
  ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true);

  Canvas.Erase (COLOR2RGB (clrWhite));
  Canvas.Rectangle (1, 1, W - 1, H - 1, COLOR2RGB (clrBlack));

  int    ind = 0;
  double X   = 0.0;

  for (int i = 0; i < CNT; i++)
  {
    switch (Distr_P)
    {
    case uniform:
      X = UniformDistribution (InpP, MinP, MaxP);
      break;
    case gauss:
      X = GaussDistribution (InpP, MinP, MaxP, SigmaP);
      break;
    case power:
      X = PowerDistribution (InpP, MinP, MaxP, PowerP);
      break;
    case levi:
      X = LeviDistribution (InpP, MinP, MaxP, LeviPowerP);
      break;
    }

    if (X < InpP)
    {
      ind = (int)Scale (X, MinP, InpP,
                        0,    Size, false);
      if (ind >= Size) ind = Size - 1;
      if (ind < 0)     ind = 0;
      CountL [ind] += 1;
    }
    else
    {
      ind = (int)Scale (X, InpP, MaxP,
                        0,    Size, false);
      if (ind >= Size) ind = Size - 1;
      if (ind < 0)     ind = 0;
      CountR [ind] += 1;
    }
  }

  int minCNT = CNT;
  int maxCNT = 0;

  for (int i = 0; i < Size; i++)
  {
    if (CountL [i] > maxCNT) maxCNT = CountL [i];
    if (CountR [i] > maxCNT) maxCNT = CountR [i];

    if (CountL [i] < minCNT) minCNT = CountL [i];
    if (CountR [i] < minCNT) minCNT = CountR [i];
  }

  int x = 0.0;
  int y = 0.0;
  color clrF;
  int centre = 0;
  int stepL  = 0;
  int stH_L  = 0;
  int stepR  = 0;
  int stH_R  = 0;

  centre = (int)Scale (InpP, MinP, MaxP, 10, W - 11, false);

  stepL = (centre - O) / Size;
  stH_L = stepL / 2;
  if (stH_L == 0) stH_L = 1;

  stepR = (W - O - centre) / Size;
  stH_R = stepR / 2;
  if (stH_R == 0) stH_R = 1;

  for (int i = 0; i < Size; i++)
  {
    x = (int)Scale (i,          0, Size - 1, O, centre - stH_L, false);
    y = (int)Scale (CountL [i], 0, maxCNT,   O, H - O,  true);

    clrF = DoubleToColor (CountL [i], minCNT, maxCNT, 0, 255);

    Canvas.Circle (x, y, 2, COLOR2RGB (clrF));
    Canvas.Circle (x, y, 3, COLOR2RGB (clrF));


    x = (int)Scale (i,          0, Size - 1, centre + stH_R, W - O, false);
    y = (int)Scale (CountR [i], 0, maxCNT,   O,      H - O, true);

    clrF = DoubleToColor (CountR [i], minCNT, maxCNT, 0, 255);

    Canvas.Circle (x, y, 2, COLOR2RGB (clrF));
    Canvas.Circle (x, y, 3, COLOR2RGB (clrF));
  }

  Canvas.Update ();
}
//——————————————————————————————————————————————————————————————————————————————

3.必要な分布法則を持つ乱数の構築

一様分布

一様分布は確率分布であり、与えられた区間内の確率変数のすべての値が等しい確率を持ちます。一様分布は、与えられた区間の値をとる可能性が等しい確率変数をモデル化するために広く使用されています。

図1：シフトのない数字の一様分布

一様分布は、すべての分布の中で最も実装が簡単です。ここで考慮すべき唯一の点は、単純に[min;max]の範囲で数値を生成することはできないので、[0.0;1.0]の範囲で以前に生成された乱数に応じて、Inの左側または右側に乱数を生成するということです。したがって、[min;max]に対するInのどの位置においても、左右に生成される数の確率は等しくなります。分布に範囲外やアーチファクトの問題はありません。

一様分布は、与えられた範囲内の数値を、その範囲全体に等しい確率で出現させる必要がある場合に、あらゆるケースで使用することができます。

//——————————————————————————————————————————————————————————————————————————————
double UniformDistribution (const double In, const double outMin, const double outMax)
{
  double rnd = RNDfromCI (0.0, 1.0);

  if (rnd >= 0.5) return RNDfromCI (In, outMax);
  else            return RNDfromCI (outMin, In);
}
//——————————————————————————————————————————————————————————————————————————————

正規（ガウス）分布

正規分布は、自然界、経済学、その他の分野で多くの無作為な現象を記述する確率分布です。ベル型と平均値を中心とした対称性が特徴です。正規分布の平均と分散は、それを完全に決定します。

正規分布の重要な特性の1つは、平均を中心とした対称性です。これは、確率変数が平均と等しい値をとる確率が最も大きく、平均から離れるにつれて平均と異なる値をとる確率が小さくなることを意味します。この特性により、正規分布はモデリングやデータ分析に特に有用です。平均とそれからの偏差を持つ無作為な現象を記述し予測することができるからです。

正規分布はまた、統計的手法やモデルでの使用に適した多くの数学的特性を持っています。例えば、確率変数が独立で正規分布を持つ場合、その和も正規分布を持ちます。この性質により、正規分布は多数の確率変数からなる複雑なシステムのモデリングや分析に用いることができます。正規分布は、統計学、物理学、経済学、金融、その他の分野で多く応用されており、線形回帰や時系列分析など、多くの統計的手法やモデルの基礎となっています。

最適化アルゴリズムにとって、正規分布は、数直線上の特定の位置に注意を向けたい場合に有用です。この場合、必要なのは分布形を形成する曲線の一部だけかもしれありません。例えば、標準偏差3以内の分布を使用するとします。その境界の外側にあるものに関しては、値を境界の端に押し戻すことはできません。押し戻せば、端での脱落頻度が平均値での頻度を上回ることになります。この問題を図2に示します。以下の説明で解決します。

正規分布則を持つ確率変数を生成するには、ボックス＝ミュラー法を使用することができます。

• まず、2つの一様分布の乱数u1 (0, 1]とu2 [0, 1]を生成する
• 次に、以下の式を使って確率変数z0を計算する

z0 = sqrt(-2 * ln(u1)) * cos(2 * pi * u2)   

• 結果として生じる確率変数z0は、標準正規分布を持つことになる
  

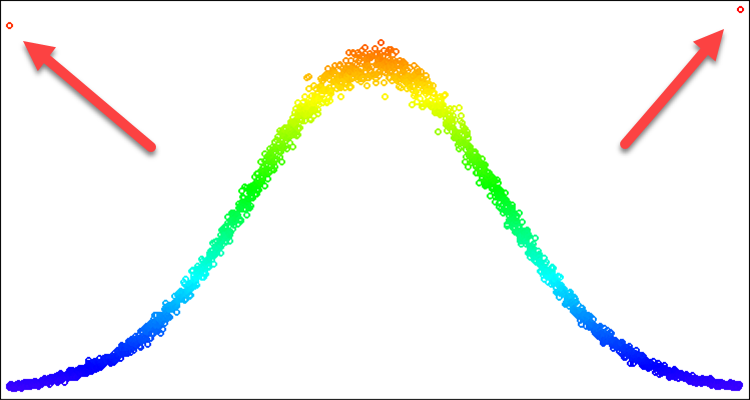
図2：シグマ=3の正規分布と、シグマ3以上のすべての削除を試みたときのアーチファクト

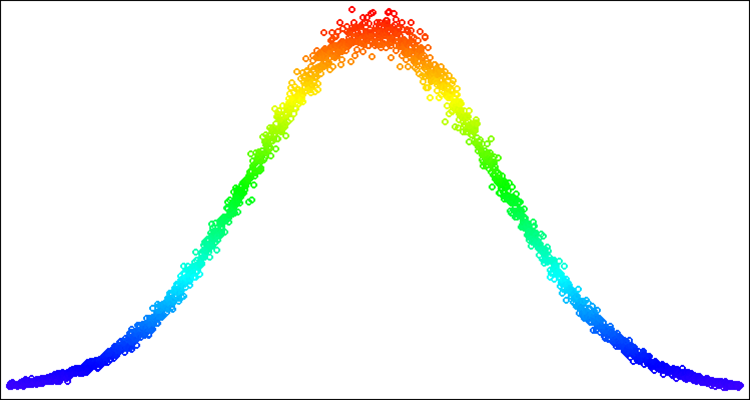
図3：シグマ=3の正規分布とアーチファクト（分布の境界を超える）の解決された問題

GaussDistribution関数を実装してみましょう。この関数は、平均値inに対して正規分布の乱数値を生成します。

• 関数パラメータ、入力値(in)、出力範囲の最小値と最大値（outMinとoutMax）、標準偏差(sigma)が設定される
• 0から1の範囲で無作為に生成されるu1の自然対数が計算される
• u1が0以下の場合、logNには0.000000000000001が割り当てられ、それ以外の場合、logNはu1に等しい
• z0値は正規分布式を用いて計算される
• 入力されたsigmaが、標準偏差の最大値8.583864105157389の範囲外かどうかが確認される
  
• z0がsigmaN以上の場合、z0には0～sigmaNの範囲の無作為な値が割り当てられ、それ以外の場合、z0が-sigmaN以下であれば、z0には-sigmaN～0.0の範囲の無作為な値が割り当てられる
• z0が0以上の場合、0～sigmaNの範囲でScale関数を使って計算された値が返され、出力範囲はin～outMaxとなり、それ以外の場合、-sigmaN～0の範囲でScale関数を使って計算された値が返され、出力範囲はoutMin～inとなる
  

黄色でハイライトされた点は、与えられた標準偏差の端における脱落頻度の問題に対する解です。したがって、境界線の外側にある確率を、分布曲線の対応する部分に「広げる」だけです。この場合、分布形状に違反することはありません。

//——————————————————————————————————————————————————————————————————————————————
double C_AO_SC::GaussDistribution (const double In, const double outMin, const double outMax, const double sigma)
{
  double logN = 0.0;
  double u1   = RNDfromCI (0.0, 1.0);
  double u2   = RNDfromCI (0.0, 1.0);

  logN = u1 <= 0.0 ? 0.000000000000001 : u1;

  double z0 = sqrt (-2 * log (logN)) * cos (2 * M_PI * u2);

  double sigmaN = sigma > 8.583864105157389 ? 8.583864105157389 : sigma;

  if (z0 >=  sigmaN) z0 = RNDfromCI (0.0,     sigmaN);
  if (z0 <= -sigmaN) z0 = RNDfromCI (-sigmaN, 0.0);

  if (z0 >= 0.0) z0 =  Scale (z0,        0.0, sigmaN, 0.0, outMax - In, false);
  else           z0 = -Scale (fabs (z0), 0.0, sigmaN, 0.0, In - outMin, false);
  
  return In + z0;
}
//——————————————————————————————————————————————————————————————————————————————

以下の図4は正規分布の乱数の例です。この例と以下の例では、-100～100の範囲内で、希望する値「50」を中心とした分布[-100;50;100]を示しています。

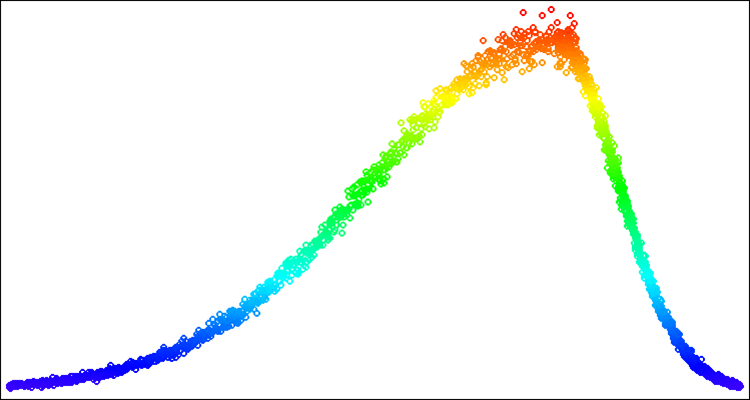
図4：シグマ=3の正規分布、[-100;50;100]

ベキ分布

ベキ分布は、非常に大きな値をとる確率が冪乗則に従って減衰する確率変数を記述する確率分布です。この分布は、パレートの法則やジプフの法則とも呼ばれます。ベキ分布は科学技術のさまざまな分野で使用されています。例えば、物理学では、星団や銀河のような多数の粒子を持つ系における質量とエネルギーの分布をモデル化するのに使用されます。経済学や社会学でも、所得や富の分配を分析するために使用されます。

ベキ分布にはいくつかの興味深い性質があります。まずは、尾が重いことです。これは確率変数が非常に大きな値をとる確率がゼロではないことを意味します。第二に、数学的な期待値が有限でないため、確率変数の平均値が無限大になる可能性があります。

ベキ分布は、最適化アルゴリズムにおいて非常に有用な形をしています。これにより、探索空間において特別な注意と明確化が必要な場所に乱数の密度を集中させることができます。しかし、正規分布の場合のように簡単に「内側に巻き込む」ことができない無限の長さの尾を持つため、純粋な形では乱数の境界を明確に制限したい場合の使用には不向きです。

ベキ分布の古典的な実装では、逆関数を使用する必要があります。しかし、既知の範囲内で値を生成するのを邪魔する分布の尾部の無限大を取り除くために、一様分布の値を冪乗したものを使用することができます。これはベキ分布を指定する正しい方法ではありませんが、理論的な分布にかなり近い形状を維持しながら、分布の末尾の無限大を取り除くことができます。確率的最適化アルゴリズムでは、これで十分です。

PowerDistribution関数は、in、outMin、outMax、powerの4つのdouble値を入力として受け取ります。これは、[-1.0;1.0]の範囲で乱数rndを生成し、power乗した結果である値rを計算し、この値を[0.0;1.0]の範囲から与えられた値の範囲にScale関数を使ってスケーリングします。rndが負数の場合、スケーリングは[outMin;in]の範囲でおこなわれ、そうでない場合は[in;outMax]の範囲でおこなわれます。関数の結果はdouble値として返されます。

• powerが1より小さい場合、結果として得られる分布の値のほとんどはゼロの近くに集中し、分布の尾は大きく切り捨てられることになるため、この分布は放物線に似ている
• powerが1の場合、得られる分布は一様になる
• powerが1より大きい場合、得られる分布の値のほとんどはゼロから遠く離れたところに分布し、分布の尾は長くなる。このような分布は重い尾を持ち、パレート分布やベキ分布に似ている
• powerが無限大に近づけば、結果として生じる分布はゼロに集中するデルタ関数に似てくる

このように、powerの異なる値を使用することで、さらなる可能性の場が広がり、特定の最適化問題を解くという文脈の中で、最適化アルゴリズムで最良の結果を得るための最適分布の選択を研究する機会が増えます。

//——————————————————————————————————————————————————————————————————————————————
double C_AO_SC::PowerDistribution (const double In, const double outMin, const double outMax, const double power)
{
  double rnd = RNDfromCI (-1.0, 1.0);
  double r   = pow (fabs (rnd), power);

  if (rnd >= 0.0) return In + Scale (r, 0.0, 1.0, 0.0, outMax - In, false);
  else            return In - Scale (r, 0.0, 1.0, 0.0, In - outMin, false);
}
//——————————————————————————————————————————————————————————————————————————————

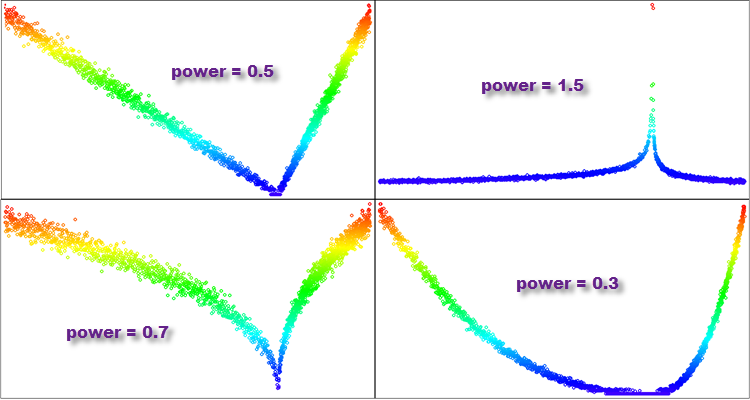
図5：さまざまなpowerを持つPowerDistribution関数の分布例

レヴィ分布

レヴィの飛行は、各ステップの長さがレヴィ分布によって決定されるランダムウォークです。

レヴィ分布は、束縛されないモーメントを持つ分布の例です。これは、非常に大きな値をとる確率が高いことを意味する重い尾を持つ確率変数を記述します。レヴィ分布では、モーメントが無限大または存在しないこともあり、正規分布のようなモーメントが限定された分布とは異なる特別な分布となっています。

レヴィ分布の重い尾とその非拘束モーメントは、極端な値や高い変動性を持つ現象のモデリングに有用です。レヴィのフライトは、物理学、金融数学、リスク分析、生態学、経済学、工学など、さまざまな分野で応用されています。例えば、拡散、乱流、プラズマ中の輸送など、物理学における無作為過程のモデルに使用できます。また、動物や集団の探索戦略をモデル化したり、工学や金融におけるパラメータの最適化にも利用できます。

レヴィ分布は、1925年にフランスの数学者ポール・レヴィによって導入され、科学技術の様々な分野で多くの応用を見出してきました。

最適化における特定のパラメータ値からの増分について話しているのであれば、レヴィフライトでは、各増分はレヴィ分布から選択され、方向は無作為に選択されます。このため、レヴィフライトでは、一部のステップが非常に長くなり、ステップ長（増分）が固定されたランダムウォークよりもパラメータ空間を高速に探索することができます。

レヴィフライト分布の形は、パワー分布の形と似ていますが、場合によっては、どちらか一方の分布を使用する方が効果的です。ベキ分布の場合と同様に、重い尾を取り除く必要があります。しかし今回は、この分布に適した別の方法でそれをおこないます。生成に関わる一様分布乱数は、[1.0;20.0]の範囲を使用するのが最適であることが実験的に発見されました。乱数の分布の最後の最小値を「冪乗」で計算する必要があります。これは、生成された数値を範囲 [0.0;1.0] にスケールするための境界として機能します。

LeviDistribution関数は入力として4つのdouble値（in、outMin、outMax、power）を取り、以下のステップを実行します。

• まず、powerパラメータに基づいて最小値minを決定する。これは、その後のスケーリングに使用できる最小の関数値になる
  
• 次に、[0.0;1.0]と[1.0;20.0]の区間上の一様分布から、それぞれ2つの乱数r1とr2を生成する
• yの値は、r2をpowerの負の冪乗に引き上げ、Scale関数を使って区間[min, 1.0]から[0.0;1.0]にスケーリングすることによって計算される
  
• 最後に、r1の値に応じて[outMin, outMax]間隔でスケーリングされた生成値を返す。r1 >= 0.5の場合、値は[in, outMax]間隔でスケーリングされ、そうでない場合は[outMin, in]間隔でスケーリングされる
  

//——————————————————————————————————————————————————————————————————————————————
double C_AO_SC::LeviDistribution (const double In, const double outMin, const double outMax, const double power)
{
  double min = pow (20.0, -power);
  double r1 = RNDfromCI (0.0, 1.0);
  double r2 = RNDfromCI (1.0, 20.0);
  
  double y = pow (r2, -power);
  y = Scale (y, min, 1.0, 0.0, 1.0, false);
 
  if (r1 >= 0.5) return In + Scale (y, 0.0, 1.0, 0.0, outMax - In, false);
  else           return In - Scale (y, 0.0, 1.0, 0.0, In - outMin, false);
}
//——————————————————————————————————————————————————————————————————————————————

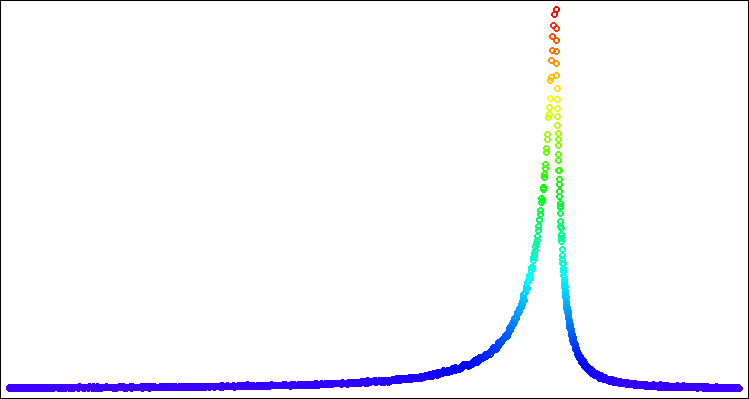
図6：リヴィ分布（power = 1.0）

4.最適化アルゴリズムテンプレート： スマート頭足類（SC、Smart Cephalopod）アルゴリズム

研究の最も興味深い段階に移りましょう。この目的のために特別に作られた最適化アルゴリズムを使用して、すべての分布を確認してみましょう。このアルゴリズムを何と呼べばいいのでしょう。

このようなアルゴリズムのアイデアをテストしてみましょう。最もおいしい場所を探している賢い頭足類を想像してみましょう。その頭は食べ物の震源地にあり、何かを食べていると仮定しましょう。同時に、触手は常に新しい餌を求めて横に広がっています。触手の1本がおいしい場所を見つけると、すぐに頭が動きます。おそらくこれは、海の生き物にインスパイアされたアルゴリズムの良いアイデアでしょう。なので、「スマート頭足類」と呼びましょう。

さまざまな分布がどのように機能し、複雑な最適化問題の解決にどのように役立つかをよりよく理解できるようになる、エキサイティングな実験になると確信しています。では、さっそくこの興味深い研究で何がわかるか見てみましょう。

頭足類の脚の特性を対応する分布法則に設定することは論理的です。そうすると、頭足類の足で新しい場所を感じるコードは次のようになります。

//----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      double X   = 0.0;
      double in  = cB [c];
      double min = rangeMin [c];
      double max = rangeMax [c];
      
      switch (distr)
      {
      case uniformDistr: X = UniformDistribution (in, min, max);         break;
      case gaussDistr:   X = GaussDistribution   (in, min, max, powers); break;
      case powerDistr:   X = PowerDistribution   (in, min, max, powers); break;
      case leviDistr:    X = LeviDistribution    (in, min, max, powers); break;
      }

      a [i].c [c] = SeInDiSp  (X, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

このコードは、popSizeのa配列の各エージェントを通過し、各座標要素に新しい値を生成する2つのネストされたループで構成されています。新しい値の生成は、4種類の分布から1つを選択し、適切な分布関数（UniformDistribution、GaussDistribution、PowerDistribution、LeviDistribution）を、現時点（頭が現在位置する場所）での最適解を表すcB配列から取り出したinの現在値に適用することによっておこなわれます。得られた新しいX値は、その要素のrangeMin値とrangeMax値、およびrangeStepを使用して、SeInDiSp関数によって正規化されます。結果の値は、指定されたエージェントと座標のa配列に格納されます。

この記事と、最適化アルゴリズムを構築するのに便利な、必要な分布を持つ乱数を生成するための具体的なクラスメソッドに取り組んだ結果、Rastrigin関数には、このテスト関数を選択した時点では明らかでなかったいくつかの重大な欠点があることが理解できたので、使用しないことにしました。古き良きRastriginはPeaks関数に取って代わられます（より完全な正当性は次回の記事で説明します）。

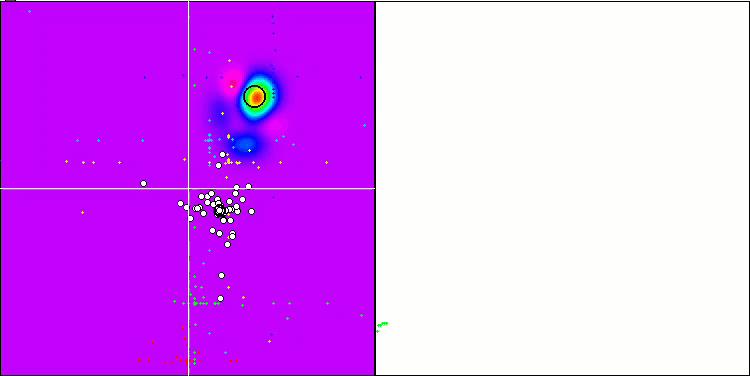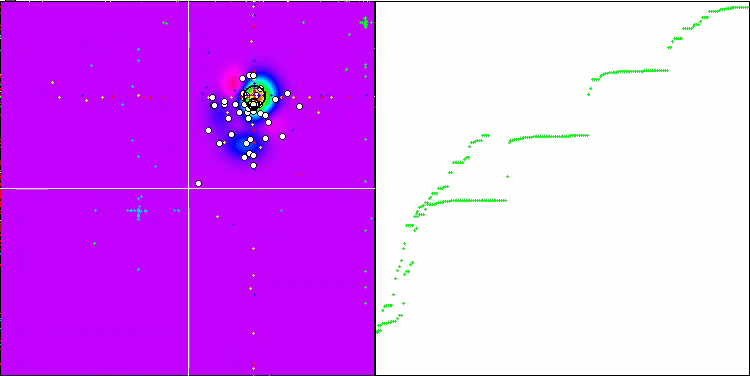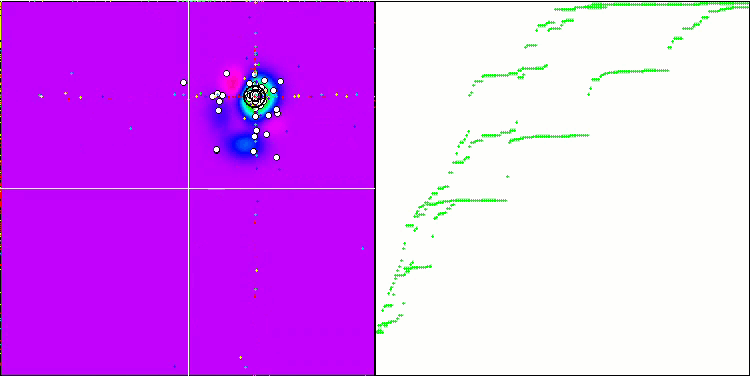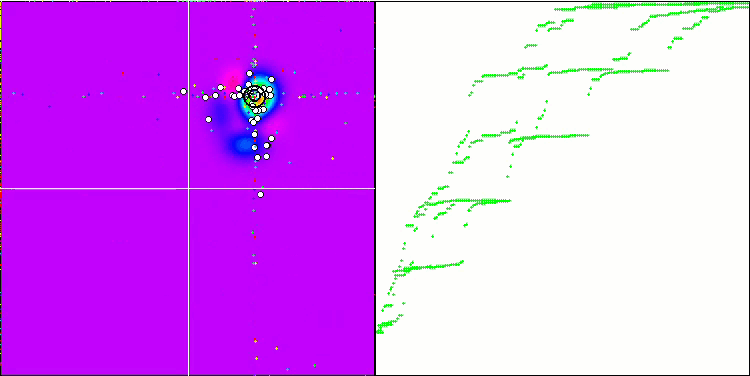
「スマート頭足類」の動き

5.まとめ

要約すると、「スマート頭足類」を使った実験は興味深い結果をもたらしました。このアニメーションは、特定の分布を適用したランダムアルゴリズムがどのようにタスクを成功させるかを示しています。どのような分布や設定が使われたかは正確には明かしませんが、この記事にあるツール一式を使ってご自分で実験してみてください。成功をコメントで共有していただけると嬉しいです。

「スマート頭足類」は、最適化をより意識するための実験に過ぎないので、評価表には考慮されません。

私の一般的な結論は、確率分布の適用と探索戦略の選択が最適化問題において重要な役割を果たすということです。なぜなら、確率的要因を考慮し、より効率的に解空間を探索し、最適解が見つかる確率の高い領域を発見することができるからです。

しかし、確率分布を使用するだけでは十分ではありません。検索戦略の選択と特徴を考慮することも重要です。最適化問題によって、異なる探索戦略には利点と欠点があります。

したがって、最適化アルゴリズムを設計する際に、特定の問題においても一般的な問題においても、より良い結果を得るためには、確率分布と探索戦略の選択を併用する必要があります。これらの要素は、開発された最適化アルゴリズムに要求される性能を提供するために、連動して機能する必要があります。全体として、この実験の結果は、最適化に対して意図的なアプローチをとることの重要性を浮き彫りにしています。例えば、最適化や最適解の発見が求められる機械学習の分野では、確率分布の適用や適切な探索戦略の選択が有効です。

この記事で紹介するツールの重要な特徴のひとつは、与えられた値の範囲内で分布をシフトさせることができることです。一般的な問題に特化した専門ライブラリには、分配シフト機能は見あたりません。これによって研究者は、最適化アルゴリズムに要求される特性に応じて確率分布を操作し、調整することができます。確率のバイアスを検索戦略の要素と一緒に調整し、コントロールすることで、実に素晴らしい効果が得られます。