Algoritmos de optimización de la población: Algoritmo de optimización de la dinámica espiral (Spiral Dynamics Optimization, SDO)

Contenido:

1. Introducción
2. Descripción del algoritmo
3. Resultados de las pruebas

1. Introducción

La literatura científica presenta una amplia variedad de algoritmos metaheurísticos de optimización basados en distintos aspectos de la naturaleza y las poblaciones. Dichos algoritmos se clasifican en varias categorías como: inteligencia de enjambre, física, química, comportamiento humano social, plantas, animales y otros. Existen numerosos algoritmos de optimización metaheurística basados en la inteligencia de enjambre. Los algoritmos basados en fenómenos físicos también se proponen y aplican ampliamente con éxito en diversos campos.

Los algoritmos basados en la inteligencia de enjambre incorporan elementos de inteligencia durante la búsqueda de una solución óptima. Así, modelan el comportamiento de un enjambre o colonia en la que los agentes individuales comparten información y cooperan para alcanzar un objetivo común. Estos algoritmos pueden ser eficaces en problemas en los que se necesita una búsqueda global y adaptabilidad a condiciones cambiantes.

Por otro lado, los algoritmos basados en la física usan como base las leyes y principios de la física para resolver problemas de optimización. Así, modelan fenómenos físicos como la gravedad, el electromagnetismo o la termodinámica y utilizan estos principios para encontrar la mejor solución. Una de las principales ventajas de los algoritmos basados en la física es su sencilla interpretación: pueden mostrar la dinámica de forma precisa y coherente en toda la zona de búsqueda.

Además, algunos algoritmos basados en la física usan la proporción áurea, una proporción matemática y natural que posee propiedades especiales y ayuda a converger a la solución óptima de forma rápida y eficaz. La proporción áurea se ha analizado y aplicado en diversos campos, como la optimización de redes neuronales artificiales, la asignación de recursos y otros.

Así pues, los algoritmos de optimización metaheurísticos basados en la física suponen una potente herramienta para resolver problemas de optimización complejos. Su precisión y la aplicación de principios físicos fundamentales las hacen atractivas para diversos campos en los que se necesita una búsqueda eficaz de soluciones óptimas.

El algoritmo de optimización de la dinámica espiral (SDO) es uno de los algoritmos físicos más simples propuesto por Tamura y Yasuda en 2011 y desarrollado utilizando el fenómeno de la espiral logarítmica en la naturaleza. El algoritmo es simple y tiene pocos parámetros de control. Además, tiene una alta velocidad de cálculo, capacidad de búsqueda local, diversificación en la fase inicial e intensificación en la fase posterior.

En la naturaleza existen muchas espirales, como galaxias, auroras, cuernos de animales, tornados, conchas marinas, caracoles, amonites, colas de camaleón y caballitos de mar. Las espirales también pueden verse en el arte antiguo creado por la humanidad en los albores de su existencia. A lo largo de los años, varios investigadores se han esforzado por comprender las secuencias y complejidades de las espirales y desarrollar ecuaciones y algoritmos para estas. Cabe destacar que un fenómeno espiral que se da con frecuencia en la naturaleza es la espiral logarítmica, que puede observarse en galaxias y ciclones tropicales. Los procesos discretos de generación de espirales se implementaron como un comportamiento de búsqueda eficiente en metaheurísticas, lo cual inspiró el desarrollo de un algoritmo de optimización de dinámica espiral.

Los ornamentos denominados secuencias espirales visibles que se encuentran en la naturaleza constituyen plantas, árboles, olas y muchas otras formas. Los patrones visuales de la naturaleza pueden modelarse usando la teoría del caos, los fractales, las espirales y otros conceptos matemáticos. En algunos patrones naturales, las espirales y los fractales se encuentran estrechamente relacionados. Por ejemplo, la espiral de Fibonacci es una variante de la espiral logarítmica basada en la proporción áurea y los números de Fibonacci. Al ser logarítmica, la curva posee el mismo aspecto a todas las escalas, por lo que también puede considerarse un fractal.

Los patrones mencionados han inspirado a los investigadores para desarrollar algoritmos de optimización. Existen distintos tipos de trayectorias en espiral, he aquí las principales:

• Espiral de Arquímedes
• Espiral cicloide
• Espiral epitrocoide
• Espiral hipotrocoide
• Espiral logarítmica
• Rosa espiral
• Espiral de Fermat

Cada uno de estos tipos de espirales tiene sus propias propiedades y puede usarse para modelar diversos patrones naturales. Se presta especial interés al descubrimiento de diversos algoritmos de optimización inspirados en la naturaleza y basados en el concepto de trayectorias en espiral. A lo largo de los años, los investigadores han desarrollado diversos algoritmos de optimización nuevos que usan el movimiento en espiral.

Además, el comportamiento de los algoritmos no espirales puede modificarse usando trayectorias espirales como superestructuras o complementos para mejorar la precisión de la solución óptima.

El algoritmo de optimización bidimensional en espiral propuesto por Tamura y Yasuda constituye un método de búsqueda metaheurística multipunto para tareas bidimensionales de optimización continua. Tamura y Yasuda propusieron entonces la optimización n-dimensional usando la filosofía de la optimización bidimensional.

2. Descripción del algoritmo

Eso sí, el algoritmo SDO de búsqueda en espacios multidimensionales descrito por los autores tiene limitaciones e inconvenientes:

• No se puede usar para problemas unidimensionales y otros problemas de optimización impares.
• La vinculación de coordenadas por pares por parte del algoritmo puede influir en la calidad de la solución en problemas específicos y mostrar falsos positivos en pruebas sintéticas.

La construcción de trayectorias en espiral en un espacio multidimensional presenta algunas dificultades. Así, si el problema se limita a un espacio unidimensional, no se podrá construir una espiral en el sentido habitual, ya que una espiral requiere movimiento en al menos dos dimensiones. En este caso, se podrá utilizar una función simple para cambiar el valor de la coordenada en el tiempo, sin utilizar una espiral. Si se trata de un problema de optimización unidimensional, entonces no se aplicará la espiral, ya que no habrá dimensiones adicionales que desplazar a lo largo de la espiral.

En un espacio multidimensional, será posible construir espirales para cada par de coordenadas, pero no se podrá definir ninguna espiral para una sola coordenada restante. Por ejemplo, en el caso de un espacio de 13 dimensiones, podremos construir espirales para 6 pares de coordenadas, pero una coordenada se moverá sin componente espiral.

El método de "espiral multidimensional" o "hiperespiral" nos permitirá construir espirales en un espacio multidimensional. Este método consiste en introducir coordenadas virtuales adicionales y definir una forma espiral en cada dimensión. Para construir la hiperespiral pueden usarse matrices de rotación y algoritmos basados en la geometría de los espacios multidimensionales. No obstante, este enfoque requiere cálculos más complejos y puede resultar difícil de aplicar en problemas prácticos de optimización.

Como en los artículos se utilizan funciones multidimensionales como funciones bidimensionales multiplicadas por duplicado, el SDO original puede mostrar resultados irrazonablemente altos, porque utiliza la unión de coordenadas por pares. Por ello, en otros problemas multidimensionales en los que las coordenadas no se encuentran relacionadas de ninguna manera, el algoritmo espiral mostrará resultados pobres. Es decir, para el algoritmo espiral del presente ejemplo, se crearán involuntariamente condiciones de "invernadero" en las funciones duplicadas.

Para evitar los problemas anteriores con el algoritmo de espiral, le proponemos un enfoque basado en la proyección de una espiral bidimensional sobre un único eje de coordenadas. Si consideramos el movimiento de un punto sobre una espiral bidimensional como el movimiento de un péndulo, entonces la proyección del movimiento del punto sobre cada una de las dos coordenadas obedecerá a la proyección del movimiento del péndulo sobre cada una de las coordenadas. Así, podremos usar la proyección del movimiento de un punto del péndulo sobre cada uno de los ejes en el espacio multidimensional para modelar el movimiento de un punto a lo largo de una espiral en el espacio bidimensional.

Al utilizar el método de construcción de espirales que modelan el comportamiento de un péndulo en cada una de las coordenadas del espacio multidimensional, el radio de cada espiral "virtual" puede ser diferente. Esto puede tener un efecto positivo en la calidad de la optimización, dado que algunas coordenadas pueden estar más cerca de los óptimos conocidos y no necesitaremos modificarlas significativamente.

Podemos tomar cualquier ley de oscilación armónica con amortiguación como una proyección de una espiral bidimensional sobre un eje unidimensional. Hemos seleccionado un oscilador armónico atenuado simple, la dependencia temporal de la posición del punto, cuya fórmula:

x(t) = A*e^(-γt)*cos(ωt + φ)

donde:

• A - amplitud de las oscilaciones
• γ - coeficiente de atenuación
• ω - frecuencia natural del oscilador
• φ - fase inicial de las oscilaciones

De la fórmula podemos deducir que el coeficiente de atenuación, la frecuencia y la fase inicial son constantes y pueden usarse como parámetros de entrada del algoritmo, pero nosotros utilizaremos dos parámetros en lugar de tres. Utilizaremos la fase inicial de las oscilaciones como componente aleatorio en cada iteración (cada coordenada estará ligeramente desplazada en fase con respecto a otras coordenadas), por lo demás el algoritmo resulta completamente determinista y solo dependerá de la colocación inicial de los puntos en el espacio.

La idea es que, en cuanto se encuentre un nuevo mejor extremo global, se calculará una nueva amplitud para todos los puntos, que será la diferencia entre la coordenada del extremo global y la coordenada del punto correspondiente. A partir de ese momento, las amplitudes en las coordenadas se individualizarán y se almacenarán en la memoria de cada punto hasta que se encuentre un nuevo extremo mejor y se determinen nuevas amplitudes.

Una vez determinadas las amplitudes, cada punto comenzará a oscilar con amortiguación; el eje de simetría de las oscilaciones será la coordenada conocida del óptimo global. Resulta visualmente cómodo evaluar la influencia de los coeficientes de atenuación y la frecuencia (parámetros externos) a partir de las figuras 1 y 2.

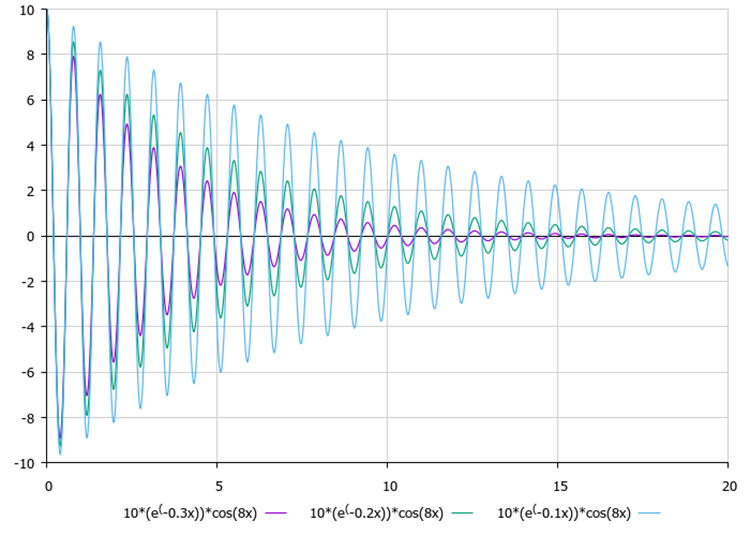
Figura 1. El efecto de la amplitud en el carácter de las oscilaciones.

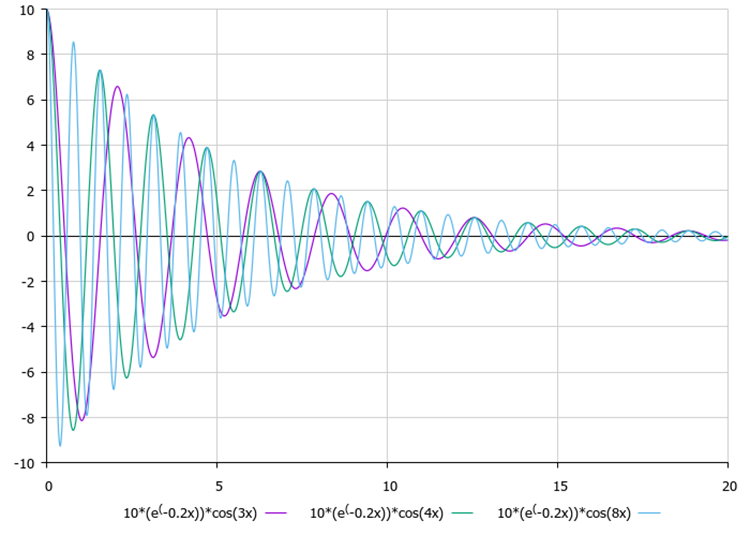
Figura 2. Influencia de la frecuencia en el carácter de las oscilaciones.

Aunque en nuestro algoritmo todas las coordenadas son completamente independientes, como hemos mencionado, no existen combinaciones de pares y conexiones entre ellas en la lógica para construir espirales; si trazáramos el movimiento de un punto en un plano bidimensional, obtendríamos una espiral del siguiente tipo, como en la figura 3.

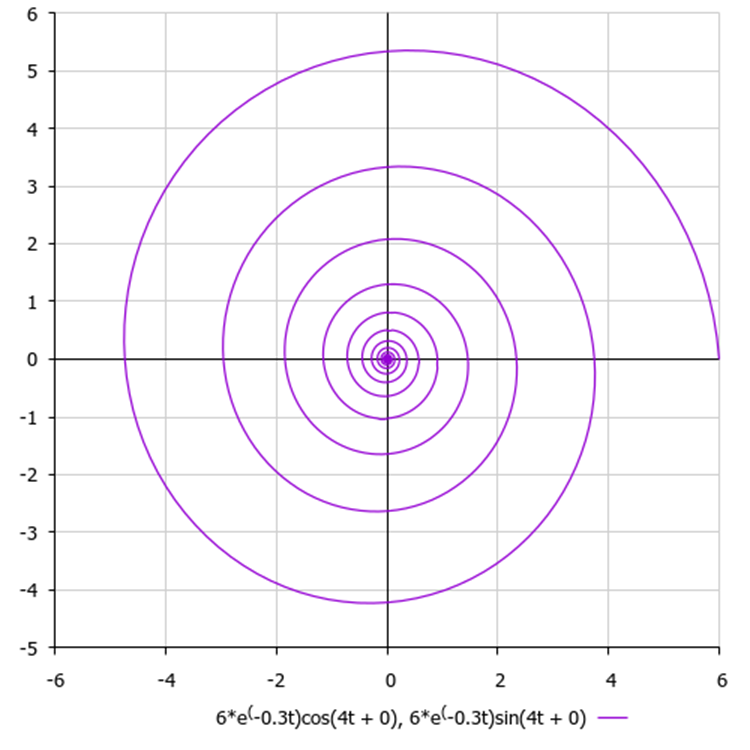
Figura 3. Una espiral hipotética con parámetros de algoritmo por defecto, donde 6 es el valor de amplitud, 0,3 es el coeficiente de atenuación y 4 es la frecuencia.

En realidad, en problemas reales, así como en funciones de prueba, las amplitudes en cada una de las coordenadas pueden ser y no tienen por qué ser iguales (a diferencia del algoritmo original). La diferencia de amplitudes ofrecerá espirales aplanadas, con la amplitud más pequeña la coordenada correspondiente se precisará más rápido ya que se encuentra más cerca del mejor valor conocido.

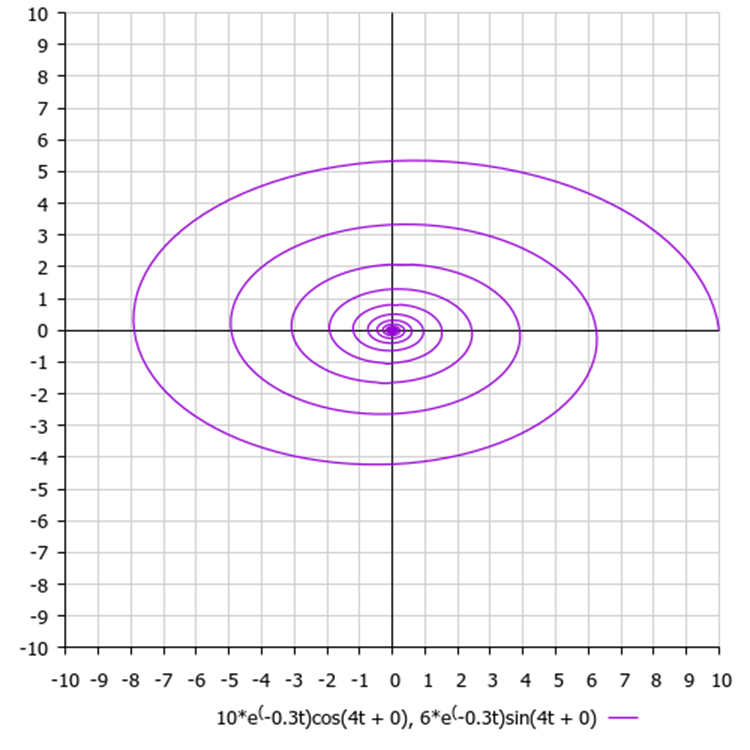
Figura 4. El valor del punto en la coordenada Y se encuentra más cerca del valor conocido y su amplitud de oscilación es menor que en el eje X.

Todos los gráficos se representan respecto a cero, pues consideramos la diferencia respecto al valor del óptimo conocido, es decir, el desplazamiento desde cero será un incremento.

Vamos a pasar a la descripción del código. En primer lugar, definiremos la estructura del algoritmo y compondremos el pseudocódigo:

1. Inicializamos la población de puntos
2. Calculamos el valor de la función de aptitud
3. Calculamos la amplitud de cada coordenada puntual cuando aparece un nuevo óptimo
4. Cuando aparezca un nuevo punto óptimo, "descartará" el punto óptimo en una dirección aleatoria
   
5. Calculamos la nueva posición de los puntos utilizando la fórmula de la oscilación armónica atenuada
6. Repetimos desde el paso 2.

El punto 4 se añade específicamente y tiene por objeto ofrecer una mayor resistencia a quedarse atascado, para que los puntos no converjan en una "espiral" hacia algún extremo local y se queden atorados allí. Los autores del algoritmo no tratan este punto.

Para describir un agente (partícula, punto), la estructura S_Particle, que contiene las siguientes variables, resultará muy adecuada:

• c [] - array de coordenadas de las partículas
  
• cD[] - array de velocidades de las partículas
• t - paso de iteración, desempeñará el papel de "tiempo" en la fórmula
  
• f - valor de la función de aptitud de la partícula
  

En la estructura también se define la función Init, que se utilizará para inicializar las variables de la estructura. El parámetro coords especificará el número de coordenadas de las partículas.

//——————————————————————————————————————————————————————————————————————————————
struct S_Particle
{
  void Init (int coords)
  {
    ArrayResize (c,    coords);
    ArrayResize (cD,   coords);
    t = 0;
    f = -DBL_MAX;
  }

  double c  []; //coordinates
  double cD []; //coordinates
  int    t;     //iteration (time)
  double f;     //fitness
};
//——————————————————————————————————————————————————————————————————————————————

Ahora definiremos la clase del algoritmo SDOm, C_AO_SDOm. La clase contendrá las siguientes variables y métodos:

• cB [] - array de las mejores coordenadas
• fB - valor de la función de aptitud de las mejores coordenadas
• p [] - array de partículas, tipo de datos - S_Particle
• rangeMax [] - array de valores máximos del rango de búsqueda
  
• rangeMin [] - array de valores mínimos del rango de búsqueda
  
• rangeStep [] - array de pasos de búsqueda
  
• Init - método para inicializar los parámetros de la clase; admite los siguientes parámetros: "coordinatesNumberP" - número de coordenadas, "populationSize" - tamaño de la población, "dampingFactorP" - coeficiente de atenuación, "frequencyP" - frecuencia, "precisionP" - precisión.
• Moving - método para desplazar partículas en el espacio de búsqueda
• Revision - método para revisar y actualizar las mejores coordenadas
• coords - número de coordenadas
• popSiz - tamaño de la población
• A, e, γ, ω, φ - componentes de la fórmula de la oscilación armónica atenuada
  
• precision, revision - variables privadas utilizadas dentro de la clase
• SeInDiSp - el método calcula un nuevo valor de coordenadas en el rango indicado con el tamaño de paso especificado.
  
• RNDfromCI - el método genera un número aleatorio en el rango indicado

Este código describe la clase C_AO_SDOm, que representa una implementación del algoritmo con funciones adicionales para revisar y actualizar las mejores coordenadas.

Las tres primeras variables de la clase serán el array cB que almacenará las mejores coordenadas, la variable fB que almacenará el valor de la función de aptitud de las mejores coordenadas, y el array p que almacenará los candidatos (partículas) de la población.

Las siguientes tres variables de clase son los arrays rangeMax, rangeMin y rangeStep, que almacenarán los valores máximo y mínimo del rango de búsqueda y los pasos de búsqueda, respectivamente.

Además, la clase contendrá tres métodos públicos: Init, Moving y Revision. El método Init se utilizará para inicializar los parámetros de la clase y crear la población inicial de partículas. El método Moving se utilizará para desplazar las partículas por el espacio de búsqueda. El método de revisión se usará para revisar las mejores coordenadas y actualizar sus valores.

La clase también contiene varias variables privadas que se utilizarán dentro de la clase. Se trata de las variables coords y popSize que almacenarán el número de coordenadas y el tamaño de la población respectivamente; la variable A que se utilizará en el método Moving; la variable precision que almacenará el valor de precisión, y la variable revision que será responsable de la necesidad de revisar las mejores coordenadas.

La clase contendrá varios métodos privados: Research, SeInDiSp y RNDfromCI. El método Research se utilizará para investigar nuevas coordenadas de partículas; los métodos SeInDiSp y RNDfromCI se usarán para calcular valores aleatorios dentro de un rango determinado.

"precision" - parámetro externo del algoritmo, será responsable de la discreción del movimiento a lo largo de la trayectoria de la oscilación atenuada, cuanto mayor sea el valor, con mayor precisión se reproducirá la trayectoria; los valores más pequeños provocarán la "irregularidad" de la trayectoria (esto no significa que se vaya a dar un impacto negativo en el resultado, dependerá de las características específicas de la tarea). Hemos elegido el parámetro por defecto como óptimo tras una serie de experimentos.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SDOm
{
  //----------------------------------------------------------------------------
  public: double     cB []; //best coordinates
  public: double     fB;    //FF of the best coordinates
  public: S_Particle p  []; //particles

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const double dampingFactorP,       //damping factor
                     const double frequencyP,           //frequency
                     const double precisionP);          //precision

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;   //coordinates number
  private: int    popSize;  //population size

  private: double A;
  private: double e;
  private: double γ;
  private: double ω;
  private: double φ;
  private: double precision;

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

El método Init de la clase C_AO_SDOm se utiliza para inicializar los parámetros de la clase y crear la población inicial de partículas.

Primero se utiliza "MathSrand" para reiniciar el generador de números aleatorios y la función "GetMicrosecondCount" para inicializar el generador.

A continuación, el método establecerá los valores iniciales para las variables "fB" y "revision" y las asignaciones de tamaño al array de población; asimismo, asignará los valores a las variables constantes que intervienen en la fórmula de oscilación atenuada.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDOm::Init (const int    coordinatesNumberP,   //coordinates number
                      const int    populationSizeP,      //population size
                      const double dampingFactorP,       //damping factor
                      const double frequencyP,           //frequency
                      const double precisionP)           //precision
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords  = coordinatesNumberP;
  popSize = populationSizeP;

  e = M_E;
  γ = dampingFactorP;
  ω = frequencyP;
  φ = 0.0;
  precision = precisionP;

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);

  ArrayResize (p, popSize);

  for (int i = 0; i < popSize; i++)
  {
    p [i].Init (coords);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Para desplazar las partículas en el espacio de búsqueda, utilizaremos el método Moving.

El primer bloque de código (if (!revision)) se ejecutará solo en la primera iteración y estará diseñado para colocar partículas aleatoriamente en el espacio de búsqueda. A continuación, el método establecerá "revision" en "true" para utilizar el bloque de código normal la próxima vez.

La siguiente parte del código del método se encargará de desplazar las partículas de la población. Si el valor de aptitud de la partícula actual es igual al valor de aptitud de las mejores coordenadas (p[i].f == fB), entonces las coordenadas de la partícula se actualizarán de la misma manera que en el primer bloque de código. Esto significa que una partícula será expulsada de su posición en una dirección aleatoria para evitar que todas las partículas converjan hacia un único punto.

En caso contrario, el método utilizará la variable "t" para simular el tiempo actual de cada partícula mediante un contador de iteraciones (que se pone a cero cuando se actualiza la mejor solución global). A continuación, se calcularán las coordenadas de cada partícula usando la fórmula de la oscilación armónica atenuada.

La parte comentada del código añadirá un incremento aleatorio al valor de la coordenada calculado por la fórmula y podrá utilizarse para obtener un bonito efecto visual de "fuegos artificiales". No obstante, este efecto no tendrá ningún valor práctico y no mejorará los resultados, por eso hemos comentado el código.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDOm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        p [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
        p [i].c [c] = SeInDiSp (p [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  int t = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    if  (p [i].f == fB)
    {
      for (int c = 0; c < coords; c++)
      {
        p [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
        p [i].c [c] = SeInDiSp (p [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }

      continue;
    }

    p [i].t++;
    t = p [i].t;

    for (int c = 0; c < coords; c++)
    {
      A = p [i].cD [c];
      φ = RNDfromCI (0.0, 2.0);

      p [i].c [c] = p [i].c [c] + A * pow (e, -γ * t / precision) * cos (ω * t / (precision) + φ);// + RNDfromCI (-0.01, 0.01) * (rangeMax [c] - rangeMin [c]);
      p [i].c [c] = SeInDiSp (p [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método Revision de la clase se utilizará para actualizar las mejores coordenadas y calcular la diferencia entre las coordenadas de la partícula y la mejor solución conocida. Esta diferencia servirá como amplitud inicial, y una vez encontrada una nueva mejor solución, las partículas comenzarán a realizar movimientos oscilatorios alrededor de las mejores coordenadas conocidas que se encuentren en el centro de estos movimientos.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDOm::Revision ()
{
  //----------------------------------------------------------------------------
  bool flag = false;
  for (int i = 0; i < popSize; i++)
  {
    if (p [i].f > fB)
    {
      flag = true;
      fB = p [i].f;
      ArrayCopy (cB, p [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  if (flag)
  {
    for (int i = 0; i < popSize; i++)
    {
      p [i].t = 0;

      for (int c = 0; c < coords; c++)
      {
        p [i].cD [c] = (cB [c] - p [i].c [c]);

      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Resultados de las pruebas

Impresión del algoritmo de dinámica espiral ejecutado en un banco de pruebas, aparentemente, no son malos resultados:

C_AO_SDOm:100;0.3;4.0;10000.0
=============================
5 Rastrigin's; Func runs 10000 result: 76.22736727464056
Score: 0.94450
25 Rastrigin's; Func runs 10000 result: 64.5695106264092
Score: 0.80005
500 Rastrigin's; Func runs 10000 result: 47.607500083305425
Score: 0.58988
=============================
5 Forest's; Func runs 10000 result: 1.3265635010116805
Score: 0.75037
25 Forest's; Func runs 10000 result: 0.5448141810532924
Score: 0.30817
500 Forest's; Func runs 10000 result: 0.12178250603909949
Score: 0.06889
=============================
5 Megacity's; Func runs 10000 result: 5.359999999999999
Score: 0.44667
25 Megacity's; Func runs 10000 result: 1.552
Score: 0.12933
500 Megacity's; Func runs 10000 result: 0.38160000000000005
Score: 0.03180
=============================
All score: 4.06967

La visualización del algoritmo SDOm ha revelado algunas características distintivas: el gráfico de convergencia en todas las funciones de prueba es inestable, la naturaleza de la curva de convergencia cambia a lo largo de las iteraciones y esto no aumenta la sensación de confianza en los resultados. En la visualización de Megacity hemos mostrado varias pruebas repetidas a propósito (normalmente solo se muestra una prueba en el vídeo, para que el GIF no resulte demasiado voluminoso): para ilustrar la inestabilidad de los resultados de una prueba a otra, la variación de los resultados es muy grande.

No se observan peculiaridades en el carácter del desplazamiento de las partículas, salvo en el caso de Forest aguda y Megacity discreta, donde las coordenadas de las partículas se alinean en líneas bien marcadas. Resulta complicado juzgar si esto es bueno o malo, por ejemplo, en el caso del algoritmo ACOm era un signo de convergencia cualitativa, pero en el caso de SDOm no puede decirse lo mismo.

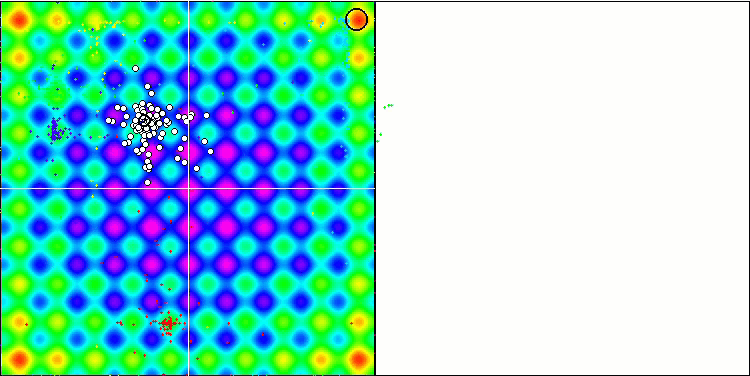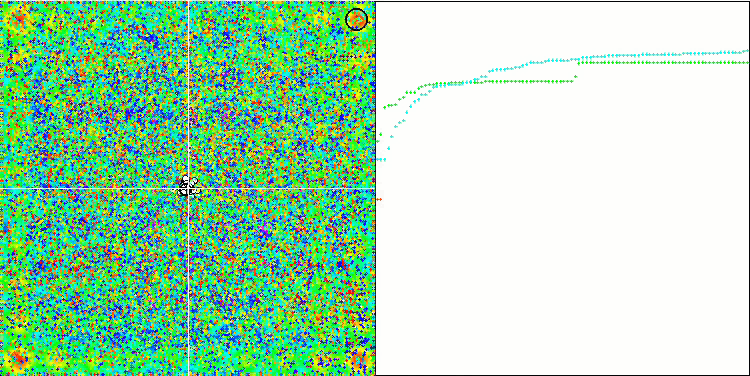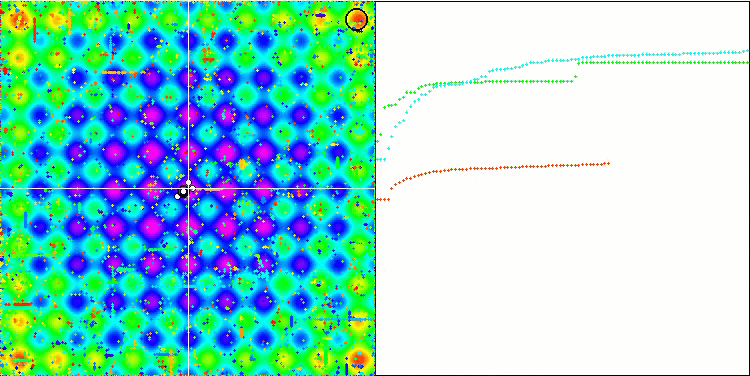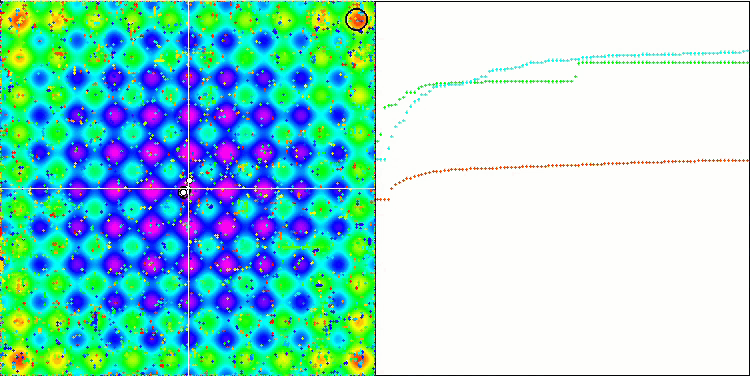
  SDOm en la función de prueba Rastrigin.

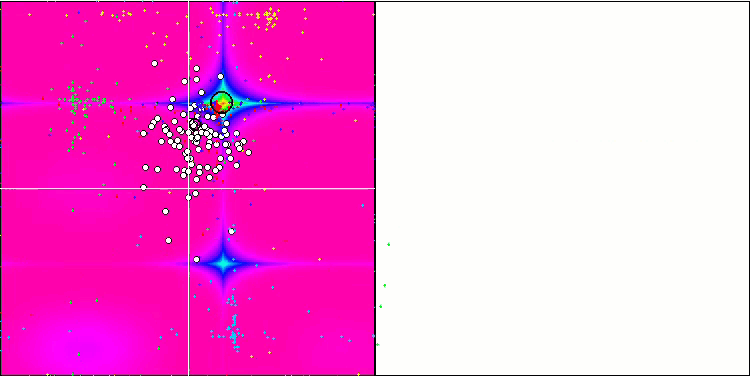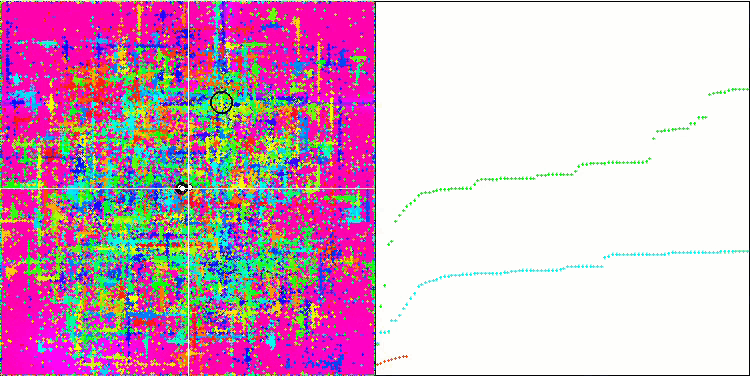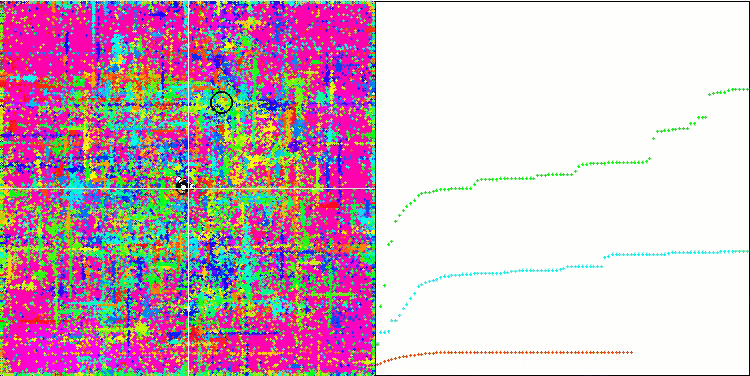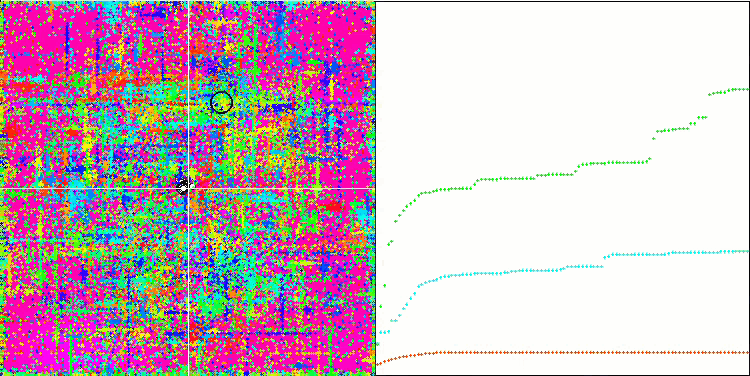
  SDOm en la función de prueba Forest.

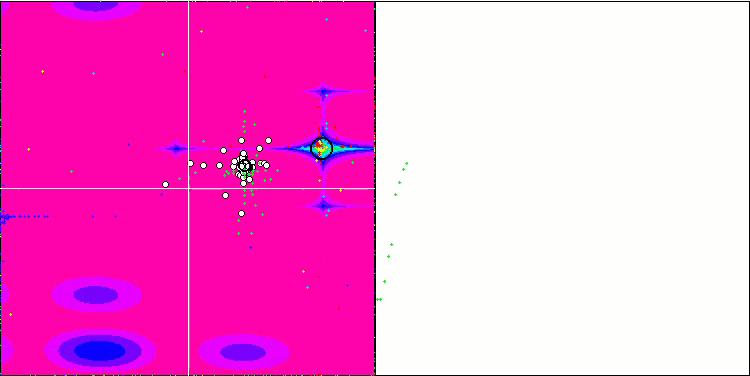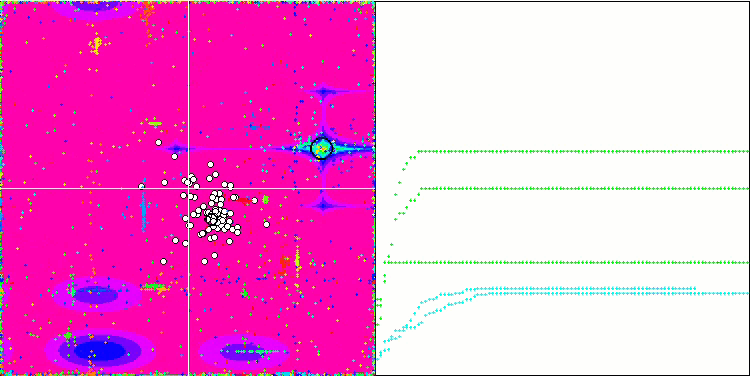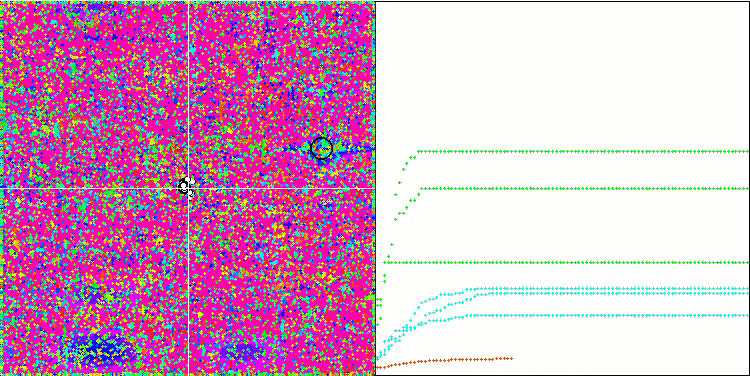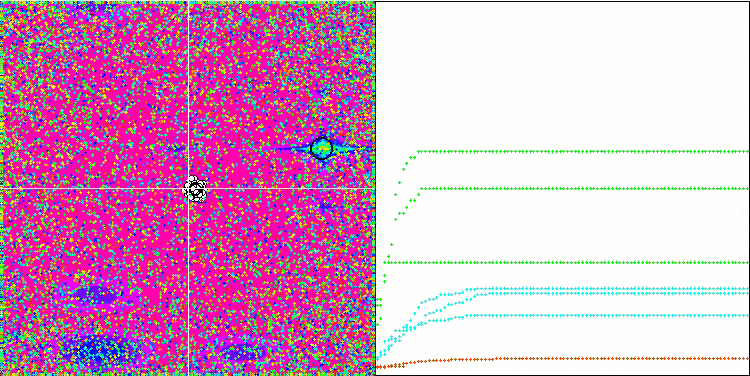
  SDOm en la función de prueba Megacity.

Al utilizar el código comentado en el método Moving, que se encarga de añadir ruido aleatorio a la coordenada de la partícula, se produce un interesante fenómeno similar al de los fuegos artificiales, sin que se utilice ningún cambio de fase de oscilación aleatoria. Supongo que tras la convergencia en masa de las partículas hacia una solución conocida, se produce una eyección de partículas en diferentes direcciones: esta es la razón del bonito efecto que muestra el atasco del algoritmo. Esto puede verse por el hecho de que el momento de la explosión de los fuegos artificiales coincide con el comienzo de la sección horizontal del gráfico de convergencia.

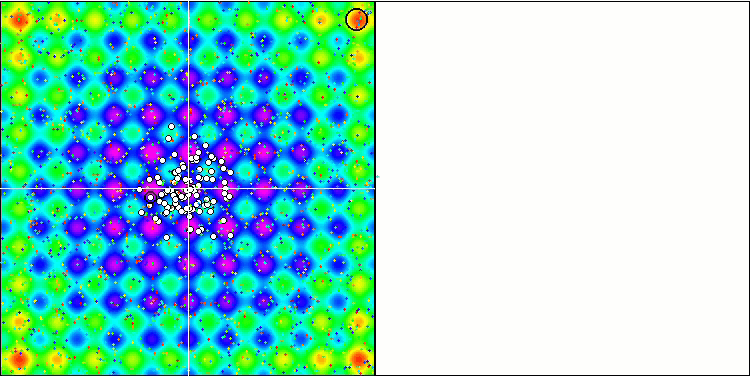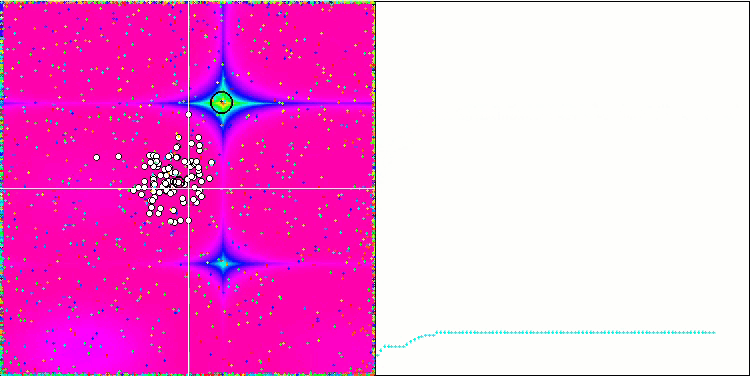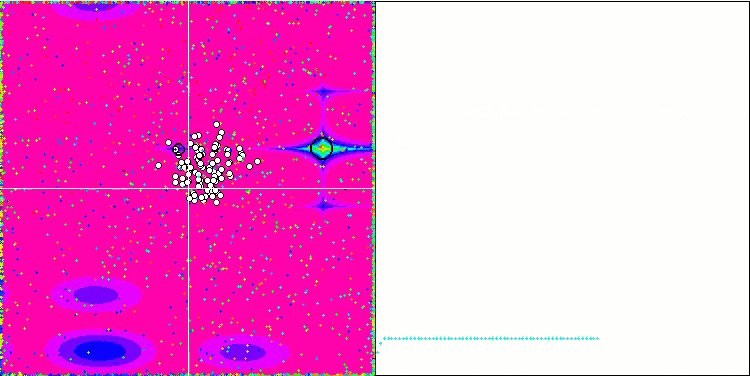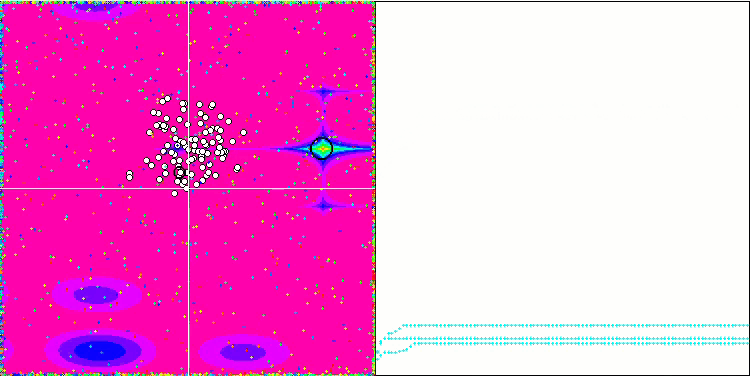
La demostración del inútil, pero el efecto de "fuegos artificiales" es bastante hermoso.

El algoritmo SDOm ha funcionado bastante bien en general, ocupando el octavo puesto de la tabla de clasificación de los 23 participantes en la revisión. El SDOm funciona notablemente mejor en la función Rastrigin suave. La tendencia a atascarse no favorece la obtención de resultados excelentes en las desafiantes características de Forest y Megacity.

№	AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	SDSm	stochastic diffusion search M	0,99809	1,00000	0,69149	2,68958	1,00000	1,00000	1,00000	3,00000	1,00000	1,00000	1,00000	3,00000	100,000
2	SDS	stochastic Diffusion Search	0,99737	0,97322	0,58904	2,55963	0,96778	0,93572	0,79649	2,69999	0,78696	0,93815	0,71804	2,44315	88,208
3	SSG	saplings sowing and growing	1,00000	0,92761	0,51630	2,44391	0,72654	0,65201	0,83760	2,21615	0,54782	0,61841	0,99522	2,16146	77,678
4	HS	harmony search	0,99676	0,88385	0,44686	2,32747	0,99882	0,68242	0,37529	2,05653	0,71739	0,71842	0,41338	1,84919	70,647
5	IWO	invasive weed optimization	0,95828	0,62227	0,27647	1,85703	0,70690	0,31972	0,26613	1,29275	0,57391	0,30527	0,33130	1,21048	48,267
6	ACOm	ant colony optimization M	0,34611	0,16683	0,15808	0,67103	0,86785	0,68980	0,64798	2,20563	0,71739	0,63947	0,05579	1,41265	47,419
7	MEC	mind evolutionary computation	0,99270	0,47345	0,21148	1,67763	0,60691	0,28046	0,21324	1,10061	0,66957	0,30000	0,26045	1,23002	44,061
8	SDOm	spiral dynamics optimization M	0,81076	0,56474	0,35334	1,72884	0,72333	0,30644	0,30985	1,33963	0,43479	0,13289	0,14695	0,71463	41,370
9	COAm	cuckoo optimization algorithm M	0,92400	0,43407	0,24120	1,59927	0,58309	0,23477	0,13842	0,95629	0,52174	0,24079	0,17001	0,93254	37,845
10	FAm	firefly algorithm M	0,59825	0,31520	0,15893	1,07239	0,51012	0,29178	0,41704	1,21894	0,24783	0,20526	0,35090	0,80398	33,152
11	ABC	artificial bee colony	0,78170	0,30347	0,19313	1,27829	0,53774	0,14799	0,11177	0,79750	0,40435	0,19474	0,13859	0,73768	29,784
12	BA	bat algorithm	0,40526	0,59145	0,78330	1,78002	0,20817	0,12056	0,21769	0,54641	0,21305	0,07632	0,17288	0,46225	29,488
13	CSS	charged system search	0,56605	0,68683	1,00000	2,25289	0,14065	0,01853	0,13638	0,29555	0,07392	0,00000	0,03465	0,10856	27,914
14	GSA	gravitational search algorithm	0,70167	0,41944	0,00000	1,12111	0,31623	0,25120	0,27812	0,84554	0,42609	0,25525	0,00000	0,68134	27,807
15	BFO	bacterial foraging optimization	0,67203	0,28721	0,10957	1,06881	0,39655	0,18364	0,17298	0,75317	0,37392	0,24211	0,18841	0,80444	27,549
16	EM	electroMagnetism-like algorithm	0,12235	0,42928	0,92752	1,47915	0,00000	0,02413	0,29215	0,31628	0,00000	0,00527	0,10872	0,11399	18,981
17	SFL	shuffled frog-leaping	0,40072	0,22021	0,24624	0,86717	0,20129	0,02861	0,02221	0,25211	0,19565	0,04474	0,06607	0,30646	13,201
18	MA	monkey algorithm	0,33192	0,31029	0,13582	0,77804	0,10000	0,05443	0,07482	0,22926	0,15652	0,03553	0,10669	0,29874	11,771
19	SFS	fish school search	0,46812	0,23502	0,10483	0,80798	0,12825	0,03458	0,05458	0,21741	0,12175	0,03947	0,08244	0,24366	11,329
20	IWDm	intelligent water drops M	0,26459	0,13013	0,07500	0,46972	0,28568	0,05445	0,05112	0,39126	0,22609	0,05659	0,05054	0,33322	10,434
21	PSO	particle swarm optimisation	0,20449	0,07607	0,06641	0,34696	0,18873	0,07233	0,18207	0,44313	0,16956	0,04737	0,01947	0,23641	8,431
22	RND	random	0,16826	0,09038	0,07438	0,33302	0,13480	0,03318	0,03949	0,20747	0,12175	0,03290	0,04898	0,20363	5,056
23	GWO	grey wolf optimizer	0,00000	0,00000	0,02093	0,02093	0,06562	0,00000	0,00000	0,06562	0,23478	0,05789	0,02545	0,31812	1,000

Conclusiones

El enfoque original de la implementación de la versión modificada ha permitido evitar cálculos matriciales pesados como en el algoritmo original del autor, y también ha permitido hacerlo universal sin vincularse a las relaciones entre coordenadas para un espacio n-dimensional.

Hemos intentado utilizar los conceptos de "masa" en la fórmula de la oscilación armónica atenuada, para que el comportamiento individual de las partículas dependa de su aptitud. La idea era reducir la amplitud y la frecuencia a las partículas con más masa (con un mejor valor de la función de aptitud), ya que las partículas más ligeras deberían realizar movimientos más amplios en amplitud y con una frecuencia más alta. Esto podría ofrecer un mayor grado de precisión en las mejores soluciones conocidas y, al mismo tiempo, aumentar la capacidad de búsqueda gracias a los "amplios" movimientos de las partículas ligeras. Desgraciadamente, en las pruebas, esta idea no ha producido la mejora esperada en los resultados.

El modelado físico de las trayectorias de las partículas en el algoritmo sugiere la posibilidad de aplicar conceptos físicos como la velocidad, la aceleración y la inercia. Se trata de una cuestión que debemos seguir investigando para un algoritmo tan interesante como el SDO.

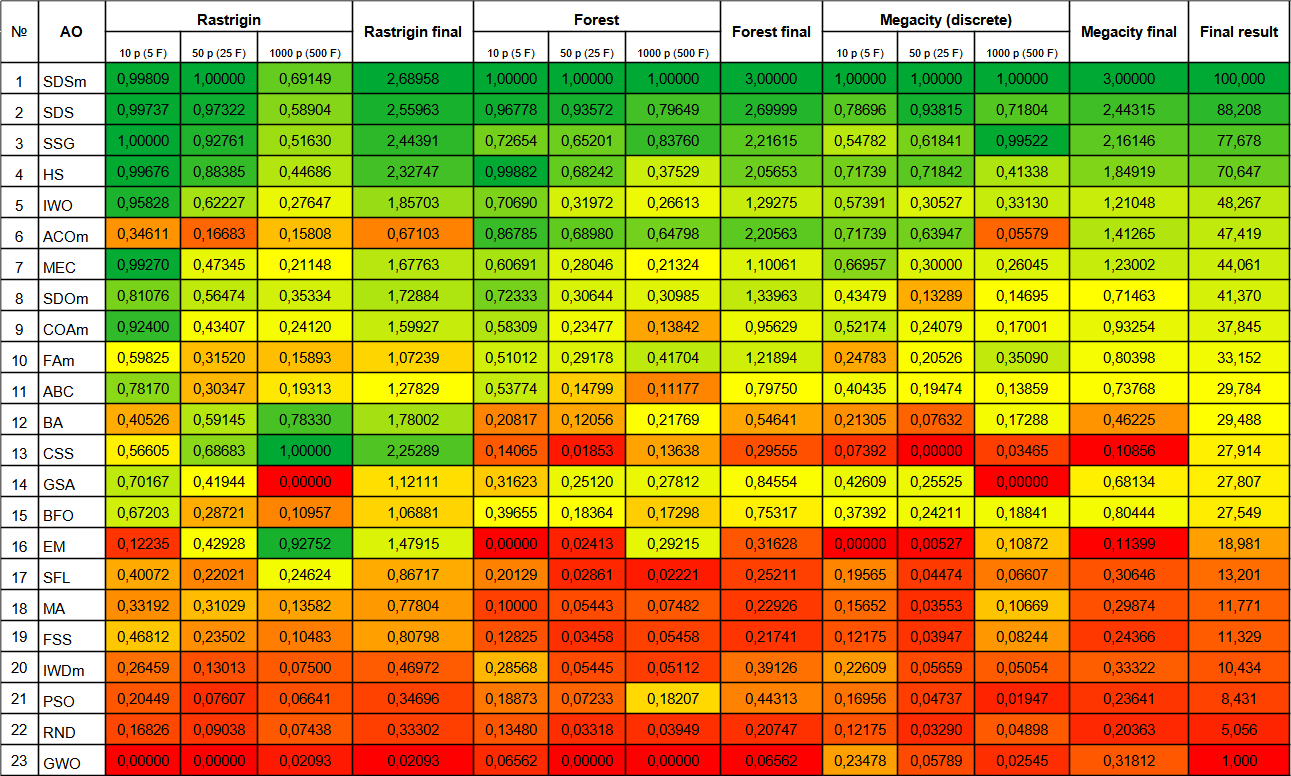
Figura 5. Clasificación por colores de los algoritmos según sus pruebas respectivas.

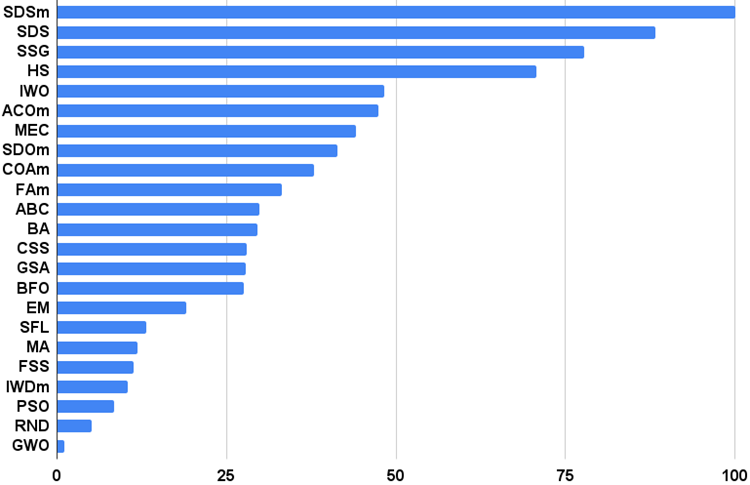
Figura 6. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor),

en el archivo hay un script para calcular la tabla de clasificación según la metodología de este artículo).

Ventajas e inconvenientes del algoritmo de optimización de la dinámica espiral modificada (SDOm):

Ventajas:
1. Número reducido de parámetros externos.
2. Aplicación sencilla.
3. Velocidad de funcionamiento.

Desventajas:
1. Gran variación de los resultados.
2. Tendencia a estancarse en los extremos locales.

Adjunto al artículo hay un archivo con las versiones reales actualizadas de los códigos de los algoritmos descritos en los artículos anteriores. El autor del presente artículo no se responsabiliza de la exactitud absoluta en la descripción de los algoritmos canónicos; muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos efectuados.