3. Sonra, üçgenlerdeki çubukların sayısını 7'ye çıkarmaya karar verdim, senaryoyu biraz elden geçirdim:
// Скрипт для подсчёта соотношения чисел затухающих и разгорающихся треугольников // // Skript OtnoshZatRazTreug, июнь 2012 // Примечание: скрипт может немного подвисать на ТФ M1. #property copyright "Copyright © Svinotavr-2000" #property link "DmitriyN" //#property show_inputs int start() { // Декларация double DliPer; // Длительность периода исследования, лет double n; // Количество бар, шт double KolZatTre; // Количество затухающих треугольников, шт double KolRazTre; // Количество разгорающихся треугольников, шт double OtnoshZatRaz; // Отношение числа затухающих треугольников к числу разгорающихся, раз double Pogreshnost; // Погрешность исследования, % // Берём число бар на 6 меньшее, чем всего n= Bars - 6 ; // Цикл по всем барам for ( int j = 0 ; j < n; j++) { // Считаем количество ЗАТУХАЮЩИХ треугольников =========== // Проверяем, являются ли High баров после начального бара (j+5) // _ меньше либо равными High начального бара (j+5) if (High[j+ 6 ] >= High[j+ 5 ]) { if (High[j+ 6 ] >= High[j+ 4 ]) { if (High[j+ 6 ] >= High[j+ 3 ]) { if (High[j+ 6 ] >= High[j+ 2 ]) { if (High[j+ 6 ] >= High[j+ 1 ]) { if (High[j+ 6 ] >= High[j]) { // Проверяем, являются ли Low баров после начального бара (j+5) // _ больше либо равными Low начального бара (j+5) if (Low[j+ 6 ] <= Low[j+ 5 ]) { if (Low[j+ 6 ] <= Low[j+ 4 ]) { if (Low[j+ 6 ] <= Low[j+ 3 ]) { if (Low[j+ 6 ] <= Low[j+ 2 ]) { if (Low[j+ 6 ] <= Low[j+ 1 ]) { if (Low[j+ 6 ] <= Low[j]) { KolZatTre=KolZatTre+ 1 ; }}}}}} }}}}}} // Считаем количество РАЗГОРАЮЩИХСЯ треугольников =========== // Проверяем, являются ли High баров после начального бара (j+5) // _ больше либо равными High начального бара (j+5) if (High[j+ 6 ] <= High[j+ 5 ]) { if (High[j+ 6 ] <= High[j+ 4 ]) { if (High[j+ 6 ] <= High[j+ 3 ]) { if (High[j+ 6 ] <= High[j+ 2 ]) { if (High[j+ 6 ] <= High[j+ 1 ]) { if (High[j+ 6 ] <= High[j]) { // Проверяем, являются ли Low баров после начального бара (j+5) // _ меньше либо равными Low начального бара (j+5) if (Low[j+ 6 ] >= Low[j+ 5 ]) { if (Low[j+ 6 ] >= Low[j+ 4 ]) { if (Low[j+ 6 ] >= Low[j+ 3 ]) { if (Low[j+ 6 ] >= Low[j+ 2 ]) { if (Low[j+ 6 ] >= Low[j+ 1 ]) { if (Low[j+ 6 ] >= Low[j]) { KolRazTre=KolRazTre+ 1 ; }}}}}} }}}}}} } // Вычисляем длительность периода истории исследования (календарный) DliPer = n* Period ()/( 1440 * 365 ); // Считаем отношение числа затухающих треугольников к разгорающимся OtnoshZatRaz=KolZatTre/KolRazTre; // Вычисляем погрешность расчётов Pogreshnost=( 1 /(KolZatTre) + 1 /(KolRazTre))* 100 ; // Формируем строки для печати string S0 = "\n" + "================= Результаты расчётов =================" + "\n" + "\n" ; string S1 = "Исследовано бар = " + DoubleToStr (n, 0 )+ " шт" + "\n" ; string S2 = "Длительность периода исследования = " + DoubleToStr (DliPer, 1 )+ " лет" + "\n" ; string S3 = "Погрешность расчётов = " + DoubleToStr (Pogreshnost, 3 )+ " %" + "\n" ; string S4 = "Отношение числа затухающих треугольников к разгорающимся = " + DoubleToStr (OtnoshZatRaz, 3 )+ " раз" + "\n" ; string S5 = "Число затухающих треугольников = " + DoubleToStr (KolZatTre, 0 )+ " шт" + "\n" ; string S6 = "Число разгорающихся треугольников = " + DoubleToStr (KolRazTre, 0 )+ " шт" ; // Выводим строки на экран Comment (S0, S1, S2, S3, S4, S5, S6); }
Komut dosyasının sonucuna bir örnek:
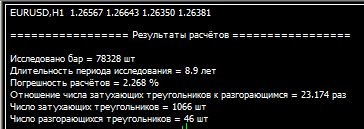
Katılıyorum,% 2'den biraz daha fazla bir hesaplama doğruluğu ile 23,1 kat fark bir model olarak adlandırmamak zor.
Bütün bunlardan nasıl bir sonuç çıkarılabilir? Sonuç - fiyatın bir yönü (yön) vardır.
Fiyat tersine çevrilirse, birçok danışmanın çalışmalarının sonuçlarının tamamen farklı olması ve büyük olasılıkla tüccarlar lehine olması oldukça olasıdır:
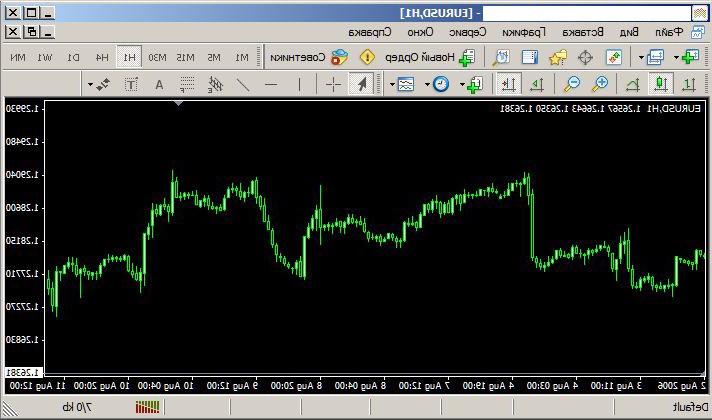
Kimin umurunda - okuyun, düşünün, deneyin ...
Bu kalıbı normal dağılımda rastgele artışlarla bir grafikte kontrol etmek isteyenler - bunun için gidin :)
Birinin yapıcı eleştirisi (kesinlikle yapıcı, ayrım gözetmeksizin) veya önerileri varsa, memnuniyetle dinlerim.
ikincisi - büyük olasılıkla solma üçgenleri dediğiniz şey ve hatta saatlerce - bu sadece mumların oynaklığında dönemsel bir düşüş :-)
ve dahası, şimdiye kadar - tabiri caizse - başlangıç noktalarını buldunuz - ama onların arkasında - çubukların davranışı (hareket yönü) - yaklaşık 50/50 olacak ... o zaman - tüm bunların pratik bir değeri yok :-) (MM hariç :- ) IMHO..
Birinin yapıcı eleştirisi (kesinlikle yapıcı, ayrım gözetmeksizin) veya önerileri varsa, memnuniyetle dinlerim.
handikapta kalıp arıyorsanız, o zaman terbiyeli olun:
1. Verilerin hangi DC'den olduğunu belirtin veya karşılaştırma için farklı DC'lerden veri getirin, benim için filtre kalıpları bizi pek ilgilendirmiyor.
2. Birden fazla döviz çifti ve TF belirtin, ancak daha iyisi - yine tablette farklı çiftler ve farklı TF'ler.
Böyle bir tablo malzemesine sahip olmak, zaten konuşmak mümkün olacak ...
;)
Yukarıdaki hatalar düzeltildi.
| Zaman aralığı | Tutum, zamanlar | Kesinlik, % | Tarih dönemi, yıllar |
|---|---|---|---|
| M1 | 2.185 | 0.003 | 8.3 |
| M5 | 3.849 | 0.038 | 8.9 |
| M15 | 9.569 | 0,313 | 8.9 |
| M30 | 14.39 | 0.836 | 8.9 |
| H1 | 23.17 | 2.268 | 8.9 |
TF H4'te hata kabul edilemez derecede büyüyor - çok az veri var.
9 yıllık bir geçmiş için orada sönen üçgen sayısı 143, parlayan üçgen sayısı 1 (bir)'dir.
Büyük olasılıkla, doğruluğu hesaplama yönteminin ve üçgenleri resmileştirme algoritmasının revize edilmesi gerekecektir.
Ve senaryonuzu çok karmaşıklaştırmıyorsanız, üçgenlerin görünümünün zamansal tekrarlama sıklığını kontrol edin.
ör. işlem ayı, haftası, günü boyunca
IMHO daha pratik kullanım olurdu
Tablo 2: Çift - GBPUSD | Demo hesap | Alpari tırnak | 7 çubuk üçgen
| Zaman aralığı | Tutum, zamanlar | Kesinlik, % | Tarih dönemi, yıllar |
|---|---|---|---|
| M1 | 2.844 | 0.004 | 8.1 |
| M5 | 4.289 | 0.041 | 8.8 |
| M15 | 7.688 | 0.243 | 8.9 |
| M30 | 10.84 | 0.642 | 8.9 |
| H1 | 17.25 | 1.793 | 8.9 |
TF H4'te hata büyüktür - yaklaşık %17.3. 9 yıllık tarihteki üçgen sayısı - 161 adet / 6 adet = 26.8 kez.
Bu gönderiyi ayrı bir başlığa taşımaya karar verdim...
1. Her şey Williams'ın kitabını yeniden okumam ve çizelgedeki iç çubukların oranını kontrol etmeye karar vermemle başladı. Sonra iç ve dış çubukların payını karşılaştırmaya karar verdim, bunun sonucunda bir düzenlilik ortaya çıktı: iç çubukların payı dış çubukların payından daha yüksek.
bu deneyim olmadan açıktır. sarmaşıkta üç kavak alıyoruz - küçük, küçük, daha az.
Hangi kavaklar daha "iç" veya "dış"? elbette "iç"!
çünkü dıştakiler büyük olanlar ve açıkçası daha az büyük, uzun kavaklar var ... ugh, istatistiklerdeki çubuklar küçük, kısa olanlardan daha az. Uzun mumlar - daha az sıklıkla. Kısa - daha sık.
Model? Evet.
ve şimdi şu soruya dikkat: Peki bu bize ne veriyor?
Cevap: Izgara!
zenginleştirme tarifi:
Daraltma zincirinde küçük bir çubuk alıyoruz ve ızgarayı her iki tarafa da doldurarak yerleştiriyoruz, daha uzağa - daha fazla doldurma. İlk kimin yönünde kar için oynayacak - kazandı.
2. Ayrıca, bu mantığı izleyerek iç ve dış üçgenlerin oranını araştırmaya karar verdim. İç üçgenlerin solması ve dış üçgenlerin parlaması olarak adlandırdım.
Bu amaçla basit bir komut dosyası yazılmıştır:
Bu üçgenlerin noktalarında boyut hakkında istatistik toplamak güzel olurdu ve çok iyi olurdu - oluşum zamanına (gününe) göre.
Haberlerde solma üçgenlerinin göründüğünü varsayacağım.
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz
Bu gönderiyi ayrı bir başlığa taşımaya karar verdim...
1. Her şey Williams'ın kitabını yeniden okumam ve çizelgedeki iç çubukların oranını kontrol etmeye karar vermemle başladı. Sonra iç ve dış çubukların payını karşılaştırmaya karar verdim, bunun sonucunda bir düzenlilik ortaya çıktı: iç çubukların payı dış çubukların payından daha yüksek.
Size iç ve dış çubukların ne olduğunu hatırlatayım:
Yukarıdaki ekranda: A çubuğu için B çubuğu dışarıda ve R çubuğu için F çubuğu içeride.
Bu alandaki araştırmalar için basit bir komut dosyası yazılmıştır:
Komut dosyasının sonucuna bir örnek:
2. Ayrıca, bu mantığı izleyerek iç ve dış üçgenlerin oranını araştırmaya karar verdim. İç üçgenlerin solması ve dış üçgenlerin parlaması olarak adlandırdım.
Bu amaçla basit bir komut dosyası yazılmıştır:
Yukarıdaki komut dosyası 6 (altı) çubuk üçgeni analiz etti. Bu scriptte hesaplama hatasını hesaplamak için çok basit bir yol eklenmiştir.
Komut dosyasının sonucuna bir örnek:
Solan ve parıldayan üçgenlerin ne olduğunu size hatırlatmama izin verin. Solan üçgen (1) ve dışa doğru açılan bir üçgen (2) örneği:
1).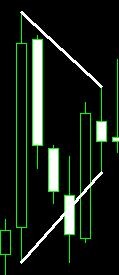 2).
2). 