[Arşiv] Ticaretle ilgisi olmayan saf matematik, fizik, kimya vb. beyin jimnastiği bulmacaları - sayfa 309

Yeni yorum
 

Kısacası, cevap (337) birdir.

 
Gerekçe, Richie ?
Onlar. Yüzüncü sırada duran birimin birinci veya ikinci kez hiçbir yere hareket etmeyeceği böyle bir sayı düzenini adlandırabilir misiniz?
PS Görev, bu konudaki ilkini biraz andırıyor (Petya hakkında): Yeterli koşul yok gibi görünüyor ve hemen hemen her sayı uygundur.
 

Şimdi anladım. Düşüneceğim :) Sadece yarın, artık düşünmüyorum.

 
Mathemat >> :
Ну ты даешь. Я надеялся на интригу...
Доказывай.

Evet, nasıl kanıtlayacağımı bilmiyorum .. Ve bundan hoşlanmıyorum ... Eh, benim değil ... Benim işim cevap aramak. // Ve bul!... :)

// Saçmalık. Ama sevilmeden önce. Ekmek vermeyin, eskiden öyleydi, bırakın bir şey ispatlayayım.

.....

Lan deneyeceğim. İlk olarak, "100"ü 100. sırada bulmanın hareketsizlik için hala yeterli bir koşul değil, sadece gerekli bir koşul olduğuna dikkat çekeceğim.

Ayrıca, yüzden küçük tüm sayılar başlangıçta 100'den küçük yerlerde olmalıdır (herhangi bir sırayla). Gerisi, sırasıyla, kalanlarda - ayrıca herhangi bir sırayla.

Çelişkiyle kanıtlamaya çalışacağım. // Çok kötüyüm.

1..99 >= 100 yerlerinde en az bir sayı varsa, ilk geçiş sırasında sıralama işlemi tarafından yakalanacak ve daha da büyük bir sayı ile karşılaşana kadar soldan sağa hareket edecektir. Bu olursa, "buluşma noktasında" kalır ve bunun yerine sağa yeni bir maksimum sayı sürünür. "Sınırı" (100) geçtikten sonra, maksimum sayı, ondan daha az olduğu ortaya çıkarsa, orada duran sayıyı kaçınılmaz olarak "hareket ettirecektir". Bu noktada, ilk geçişin analizi durdurulabilir ve ikincisine geçilebilir. 101..1982 "yer sayısı" aralığındaki en az bir sayı 100'den küçük veya eşitse, işlem tarafından yakalanacak ve sola doğru hareket etmeye başlayacaktır....vb. (aynadaki ilk geçişin açıklamasına bakın). Bu nedenle, 100 sayısını sabit bırakmanın tek bir yolu vardır: 100 sayısını oraya koyun ve 100'den küçük tüm sayıların - 100'ün soluna ve tüm büyüklerin - sırasıyla sağa ve net bir ön gruplandırmasını sağlayın.

Bu konuda söyleyebileceğim tek şey bu. Bunun ne kadar kanıt olduğu hakkında hiçbir fikrim yok, ama bir nevi kanıtı sağladım. // En azından kendim için)))

 
İkna, Volodya . Ben de aynı tartışmayı yaptım. Bir koşulun gerekliliği hakkında - aha, çok kesin olarak fark edilir. Ve cevap aynı. Tamam, sıradaki:
 

Kayınvalideme göre: bu sayı 1981, 100 değil :)

 
Mathemat >> :

Hala yeterli değil. Akımın ölçüldüğü kontaklar nerede? Izgara, orijin ve ilk temastaki orijin ile yarı sonsuz olabilir. O zaman iki tane yemek için bir lokma yeterlidir.

Ve kişilerden biri ağın merkezinde bir yerdeyse, o zaman dördü yeterlidir - çevresinde.

Kabul ediyorum. Birazdan değiştireceğim. :)

Bu ifadede mümkündür.

 

Dim a, b, c, d, i, z Kadar Uzun
Özel Alt Komut1_Click()
bir = 1
b = 2
c=3
d=4
i = 1 ila 20 için
z = bir
a = a - b
b = b - c
c = c - d
d=d-z
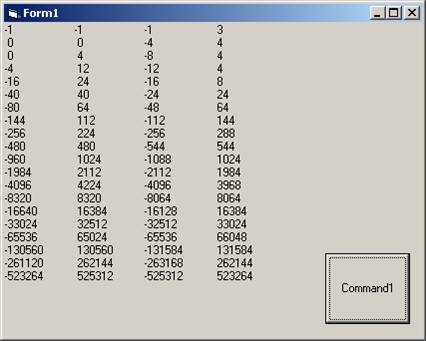
a, b, c, d yazdır
sonraki ben
son alt

 
Richie >> :

Dim a, b, c, d, i, z Kadar Uzun
Özel Alt Komut1_Click()
.......... ...
sonraki ben
son alt

.........

Şimdi kaçınılmazlığı kanıtlayın.
// Bu arada, şaşırtıcı olan gerçek şu ki, dizide çok sayıda iki kuvvet var. Ayrıca bir kaçınılmazlık?
 
Şimdi kaçınılmazlığı kanıtlayın.
Nesin sen Volodya ? Durum bu değil. Peki, Richie'den nasıl bir kanıt olabilir?
1...302303304305306307308309310311312313314315316...628
Yeni yorum