Alım-satım fırsatlarını kaçırıyorsunuz:
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Kayıt
Giriş yap
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz
Hesabınız yoksa, lütfen kaydolun
korku. insanlar o kadar aceleci sözler ki, ben bir zavallı buraya ait değilim.
Ve okuyorum - ne üzerinde anlaşacaklarını anlamaya çalışıyorum.
Bu yine bir lam ise, bir ahtapot üzerinde bir arka palto çifti çekmeye yönelik ilk girişim bir şeydir. Pratik bir şeyse yaparım.
Eh, Neutron geldi ve her şeyi yerine koydu. Bu arada pazarlamacı basıklık ve asimetriden de bahsediyor.
Karşılık gelen Gauss eğrisi herhangi bir şekilde oluşturulabilir, ancak burada sadece örnek varyansını hesaplamak ve 0 ve sigma parametreleriyle bir Gauss eğrisi oluşturmak en kolay yoldur. Daha sonra gerçek histogram ile böyle bir Gauss eğrisi arasındaki fark görülecektir.
Bu arada, bu Gauss yaklaşımı, eğrinin merkezindeki (sıfır noktasında) gerçek histogramdan önemli ölçüde düşük olmalıdır.
Urain, ne kadar s.c.o.'sun çoğaltılmış örnekler?
Öte yandan, s.c.d. güçlü bir yağ kuyruklu dağılım için numunenin boyutuna bağlıdır, bu yüzden burada o kadar basit değil.
RMS'ye hiç dokunmadım, sadece bitmiş grafiği aldım ve histograma dikey olarak sığdırmak için ölçeklendirdim.
Histogram, Klos farkının dağılımıdır (MO ve RMS'ye sahiptir), bu MO ve RMS, yukarıdaki formüle göre kırmızı çizgiyi oluşturmak için kullanılır, ancak çizgi histogramın altında kaybolduğundan ve küçük mutlak x, histogram y ile orantılı bir yapı oluşturmak için suçludur, o zaman ve karşılaştırma için her y çizgisini bir faktörle çarpmam gerekiyordu.
Referans fonksiyonu için, varyans ve MO bir dizi alıntıdan alınır (orada da hesaplanmıştır) ve aynı manipülasyonlar referansın mutlak değerleri ile gerçekleştirilir, burada her terimi katsayıya eklemeniz gerekir. köşeleri birleştirmek için.
Anladığım kadarıyla referans işlevi HP işlevidir.
Eğer öyleyse, o zaman bir şey dışında her şeyi doğru yaptınız: çarpma yapamazsınız. Zirveleri birleştirme isteğinizin, grafiklerin gerçek konumuyla hiçbir ilgisi yoktur. Ek olarak, çarpma sırasında HP işlevinin normalleştirilmesi ihlal edilir. >1 olasılığını nasıl istersiniz?
Çarpmayı kaldırır ve resmi tekrar yaparsanız, grafiklerin genişliği aşağı yukarı düzgün bir şekilde eşleşir. Bununla birlikte, histogram merkezde ve kenarlarda daha yüksek olacaktır, bu da iki ana sorunu gösterir: daha fazla tekrarlama ve aynı zamanda ağır kuyruklar.
Sakıncası yoksa böyle bir resim yapın.
not
Sorununuzu bir önceki mesajdan anlıyorum. HP'nin normalleşmesini bozmaya gerek yok. Histogram için doğru ölçeği bulmak daha iyidir. Aynı normalleşmeden. Histogramın tüm çubuklarının yüksekliklerini toplamanız ve ardından her çubuğu bu miktara bölmeniz gerekir. Sonuç, histogramınızın da 1'e normalleştirilmesidir.
Ve okuyorum - ne üzerinde anlaşacaklarını anlamaya çalışıyorum.
Bu yine bir lam ise, bir ahtapot üzerinde bir arka palto çifti çekmeye yönelik ilk girişim bir şeydir. Pratik bir şeyse yaparım.
Normal dağılımda olmayan bir dizi tırnak işaretinin birinci farkının ne olduğunu belirlemeye çalışıyorum?
Normal dağılımda olmayan bir dizi tırnak işaretinin birinci farkının ne olduğunu belirlemeye çalışıyorum?
Ve ne verecek, hedef belirleme nedir? "Anormallik" alanlarını tanımla? Tekrar - neden?
(Yalnızca "?????")))
Ve ne verecek, hangi hedef belirleme? "Anormallik" alanlarını tanımla? Tekrar - neden?
(Yalnızca "?????")))
Anormalliğin hangi kanuna göre tezahür ettiğini araştıralım diyelim.
Anladığım kadarıyla referans işlevi HP işlevidir.
Eğer öyleyse, o zaman bir şey dışında her şeyi doğru yaptınız: çarpma yapamazsınız. Zirveleri birleştirme isteğinizin, grafiklerin gerçek konumuyla hiçbir ilgisi yoktur. Ek olarak, çarpma sırasında HP işlevinin normalleştirilmesi ihlal edilir. >1 olasılığını nasıl istersiniz?
Çarpmayı kaldırır ve resmi tekrar yaparsanız, grafiklerin genişliği aşağı yukarı düzgün bir şekilde eşleşir. Bununla birlikte, histogram merkezde ve kenarlarda daha yüksek olacaktır, bu da iki ana sorunu gösterir: daha fazla tekrarlama ve aynı zamanda ağır kuyruklar.
Sakıncası yoksa böyle bir resim yapın.
not
Sorununuzu bir önceki mesajdan anlıyorum. HP'nin normalleşmesini bozmaya gerek yok. Histogram için doğru ölçeği bulmak daha iyidir. Aynı normalleşmeden. Histogramın tüm çubuklarının yüksekliklerini toplamanız ve ardından her çubuğu bu miktara bölmeniz gerekir. Sonuç, histogramınızın da 1'e normalleştirilmesidir.
Vlob öyle yazıldığından değil. Her şeyin erken düzeltilmesi gerekiyor.
Eh, hiç düzenleme yok. Yalnızca her ikisi de Çoklu=1.0/Nokta noktasına ayarlanır; yoksa türkiye bu kadar küçük değerleri görmez.
. Sol altta olasılık dağılımı yoğunluğu, sağda - aynı zamanda logaritmik bir ölçekte.
Dağılım normal olsaydı, burada bir parabolümüz olurdu, ama yok - çünkü "şişman" kuyruklar. Prensip olarak, burada en küçük kareler yöntemini kullanarak Gauss'a girmeniz gerekir, o zaman her şey yerine oturacaktır. Optimum uyum için bir formül atmanız gerekiyor ...
Sergey, peki ya çift logaritmik? Bu düşüncenin içimi kemiren bir şey bu ilk gün değil...
Her şeyi tevazudan kontrol etmeyeceğim :)
Sergey, peki ya çift logaritmik? Bu düşüncenin içimi kemiren bir şey bu ilk gün değil...
Her şeyi tevazudan kontrol etmeyeceğim :)
Şu şekilde ortaya çıkacak:
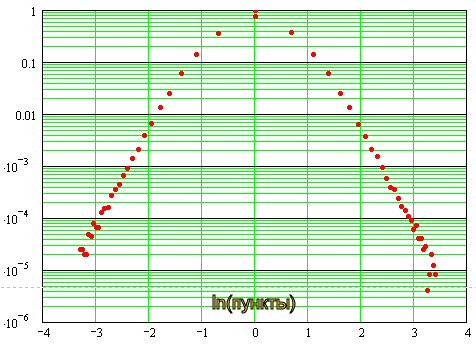
Sıfıra yakın, dağılımın normale yakın olduğu ve daha sonra çift logaritmetik ölçekte "kuyrukların" dağılımının üstel yapısını gösteren düz çizgiler şeklinde asimptotik hale geldiği görülebilir. Başka bir deyişle, onların "ağırlıkları" hakkında.