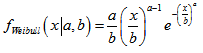#include <Graphics\Graphic.mqh>
#include <Math\Stat\Weibull.mqh>
#include <Math\Stat\Math.mqh>
#property script_show_inputs
//--- giriş parametreleri
input double a_par=1; // dağılım parametresi (şekil)
input double b_par=5; // dağılım parametresi (ölçek)
//+------------------------------------------------------------------+
//| Script program start function |
//+------------------------------------------------------------------+
void OnStart()
{
//--- fiyat çizelgesini gizle
ChartSetInteger(0,CHART_SHOW,false);
//--- rassal sayı üreticisini başlat
MathSrand(GetTickCount());
//--- rassal değişken örneğini oluştur
long chart=0;
string name="GraphicNormal";
int n=1000000; // örnekteki değerlerin sayısı
int ncells=51; // histogramdaki aralık sayısı
double x[]; // histogram aralıklarının merkezleri
double y[]; // aralığın içine düşen değerlerin sayısı
double data[]; // rassal değişken örneği
double max,min; // örnekteki maksimum ve minimum değerlerin sayısı
//--- Weibull dağılımına uyan bir örnek oluştur
MathRandomWeibull(a_par,b_par,n,data);
//--- histogramı çizmek için gereken verileri hesapla
CalculateHistogramArray(data,x,y,max,min,ncells);
//--- teorik eğriyi çizebilmek için seri sınırlarını ve adım değerini al
double step;
GetMaxMinStepValues(max,min,step);
step=MathMin(step,(max-min)/ncells);
//--- hesaplanan teorik verilerden [min,maks] aralığına düşenleri al
double x2[];
double y2[];
MathSequence(min,max,step,x2);
MathProbabilityDensityWeibull(x2,a_par,b_par,false,y2);
//--- ölçeği ayarla
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//--- çıktı çizelgeleri
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat("Weibull distribution a=%G b=%G",a_par,b_par));
graphic.BackgroundMainSize(16);
//--- X ekseninin otomatik olarak ölçeklenmesini engelle
graphic.XAxis().AutoScale(false);
graphic.XAxis().Max(max);
graphic.XAxis().Min(min);
//--- tüm eğrileri çiz
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,"Sample").HistogramWidth(6);
//--- şimdi dağılım yoğunluğunun teorik eğrisini çiz
graphic.CurveAdd(x2,y2,CURVE_LINES,"Theory");
graphic.CurvePlotAll();
//--- tüm eğrileri çiz
graphic.Update();
}
//+------------------------------------------------------------------+
//| Veri setinin frekansını ayarla |
//+------------------------------------------------------------------+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//--- aralık merkezini tanımla
for(int i=0; i<cells; i++)
{
intervals[i]=minv+i*width;
frequency[i]=0;
}
//--- aralığın içine düşme frekansını gir
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+------------------------------------------------------------------+
//| Seri oluşturma için gereken değerleri hesaplar |
//+------------------------------------------------------------------+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//--- normalleştirme kesinliğini almak için serinin tam aralığını hesapla
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//--- maksimum ve minimum değerleri belirtilen kesinlik için normalleştir
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//--- seri oluşturma aşaması belirtilen kesinliğe göre ayarlanır
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
}
|