Поздравляю автора. Очень редкая на этом сайте статья.
Автору (почему-то нет ника).
Аналогичная проблема может решаться иными способами. Существуют тесты на избыточные и пропущенные переменные. Я бы мог это сделать и сравнить с Вашими результатами. Но мне нужны все Ваши файлы в формате .csv.
...мне нужны все Ваши файлы в формате .csv.
Так вроде лежит исходник в архиве masterdata.zip
Опубликована статья Использование дискриминантного анализа для построения торговых систем:
Автор: ArtemGaleev
После того, как мы выбрали переменные, из них придется составить некоторую зависимость, в которой price будет зависимой переменной (функцией), а остальные индикаторы будут независимыми переменными. Вот схематичное уравнение:
price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)
-1 означает предыдущее значение. Это естественно, так как индикатор получается из цены аналитически. Учтем, что price - это приращение и поэтому будем брать приращения индикаторов. Из-за лени беру не все индикаторы. Оценим это уравнение методом наименьших квадратов:
Мы получили оценку коэффициентов уравнения. Очень интересный последний столбик: он означает вероятность равенства нулю соответствующего коэффициента. Это вероятность для всех коэффициентов значительно больше, чем хотя бы 10%, т.е. можно считать что мы не можем отвергнуть гипотезу о равенстве нулю соответствующего коэффициентов. Соответственно R-квадрат имеет смешную величину.
Я делаю вывод, что бесполезно заниматься классификацией индикаторов - они бесполезны, так как они не имеют отношения к приращению цены.
Или я не прав?
...Или я не прав?
Вроде правы Вы :-)
faa1947, у меня к вам вопрос. Хотел уточнить пару моментов... я вот так расчитывал данные по вашему уравнению:
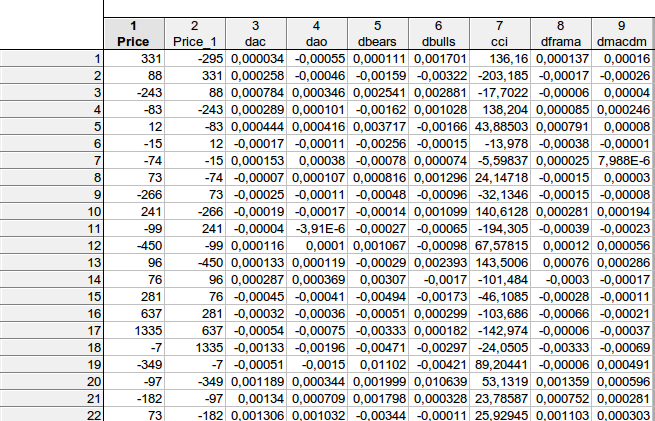
Данные из таблицы соответствуют вашему схематичному уравнению price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1) ?
И получил следующий результат:
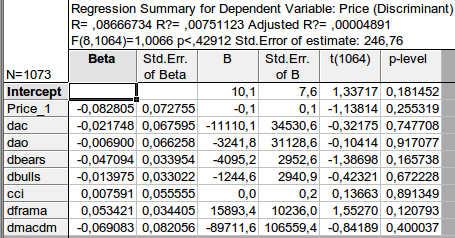
После того, как мы выбрали переменные, из них придется составить некоторую зависимость, в которой price будет зависимой переменной (функцией), а остальные индикаторы будут независимыми переменными. Вот схематичное уравнение:
price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)
-1 означает предыдущее значение. Это естественно, так как индикатор получается из цены аналитически. Учтем, что price - это приращение и поэтому будем брать приращения индикаторов. Из-за лени беру не все индикаторы. Оценим это уравнение методом наименьших квадратов:
Мы получили оценку коэффициентов уравнения. Очень интересный последний столбик: он означает вероятность равенства нулю соответствующего коэффициента. Это вероятность для всех коэффициентов значительно больше, чем хотя бы 10%, т.е. можно считать что мы не можем отвергнуть гипотезу о равенстве нулю соответствующего коэффициентов. Соответственно R-квадрат имеет смешную величину.
Я делаю вывод, что бесполезно заниматься классификацией индикаторов - они бесполезны, так как они не имеют отношения к приращению цены.
Или я не прав?
Сообщайте, пожалуйста, название стат. метода, который использовали. Это было построение линейного регрессионного уравнения, где на входе индикаторы, а на выходе будущая цена? Верно? Это не будет работать для форекс, поскольку он не является линейной детерминированной системой. У дискриминантного анализа другая задача, он строит модели для распознавания образов на основе внешних описаний системы.
Если бы классификация индикаторов для анализа приращения цены была бесполезной, то технический анализ был бы бессмысленен. К счастью, цена не ведет себя хаотично, в ней есть память о предыдущих событиях.
Вроде правы Вы :-)
faa1947, у меня к вам вопрос. Хотел уточнить пару моментов... я вот так расчитывал данные по вашему уравнению:
Данные из таблицы соответствуют вашему схематичному уравнению price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1) ?
И получил следующий результат:
Исходные данные выглядят следующим образом:
Уравнения выглядят:
Estimation Equation:
=========================
PRICE = C(1)*PRICE(-1) + C(2)*DAC(-1) + C(3)*DAO(-1) + C(4)*DBEARS(-1) + C(5)*DBULLS(-1) + C(6)*CCI(-1) + C(7)*DFRAMA(-1) + C(8)*DMACDM(-1)
Substituted Coefficients:
=========================
PRICE = -0.0228102658125*PRICE(-1) + 12005.8974278*DAC(-1) + 4033.10946937*DAO(-1) + 3176.11232129*DBEARS(-1) - 6021.36196728*DBULLS(-1) - 0.102710105369*CCI(-1) - 11487.4273249*DFRAMA(-1) + 62535.3387412*DMACDM(-1)
Я не понял Ваш расчет. У меня принципиальным является использование лаговых значение (предыдущего значения). Это дает возможность делать прогноз. Если лаг -1 соответствует 1-му наблюдению, то зависимая переменная соответствует новому, прогнозному, ненаблюдаемому наблюдению.
Что такое p-level? У меня это вероятность равенства нулю соответствующего коэффициента.
Сообщайте, пожалуйста, название стат. метода, который использовали. Это было построение линейного регрессионного уравнения, где на входе индикаторы, а на выходе будущая цена? Верно?
Произведена оценка регрессии методом наименьших квадратов. По ней можно делать прогноз.
Это не будет работать для форекс, поскольку он не является линейной детерминированной системой.
Если линейность - то это в конкретном примере. Детерминированностью не пахнет, так как даже к коэффициентам подходят как к случайной величине. Все коэф не вычисляются, а оцениваются. Во втором столбике указана стандартная ошибка оценки коэф. Прошу отметить, что она огромна.
Если бы классификация индикаторов для анализа приращения цены была бесполезной, то технический анализ был бы бессмысленен.
Именно так, и смею заверить, что я не один так думаю. ТА не является наукой, а является разновидностью астрологии. Изначально, 300 лет назад, это была система по визуализации котира. С тех пор это направление чрезвычайно развилось. Все остальное для буратин на поле чудес. Вашей статье я обрадовался, так как в ней имеется некоторая регулярная и повтОримая мысль.
Если бы классификация индикаторов для анализа приращения цены была бесполезной
Здесь проведен анализ частного случая индикаторов. Всегда надо доказывать, что конкретный индикатор или его использование имеет какое-либо отношение к котиру. ТА этот вопрос никогда не рассматривает.
К счастью, цена не ведет себя хаотично, в ней есть память о предыдущих событиях.
Вся эконометрика построена на предположении, что котир имеет детерминированную составляющую (автокорреляцию, память) и шум.
У дискриминантного анализа другая задача, он строит модели для распознавания образов на основе внешних описаний системы.
Задача понятна. Но можно ли доверять полученному результату, вот в чем вопрос. Проблема состоит не в классификации (это часть проблемы, которую тоже нужно решать), а в доверии к полученному прогнозу. Именно в этом проблема.
Я не понял Ваш расчет. У меня принципиальным является использование лаговых значение (предыдущего значения). Это дает возможность делать прогноз. Если лаг -1 соответствует 1-му наблюдению, то зависимая переменная соответствует новому, прогнозному, ненаблюдаемому наблюдению.
Что такое p-level? У меня это вероятность равенства нулю соответствующего коэффициента.
faa1947, я же привёл таблицу уже с лагами (для нескольких первых строк - всю таблицу не всунуть). Но сначала я вычислил разницы индикаторов, поэтому всего стало 1073 строки, а не 1074. Потом зависимую переменную Price передвинул на шаг вперёд.
Получилось, что, на примере 1-ой строки:
331 = C(1)*(-295) + C(2)* 0,000034+ C(3)* (-0,00055) + C(4)* 0,000111 +
C(5)* 0,001701+ C(6)*136,16+ C(7)* 0,000137+ C(8)*0,00016, при условии, что
PRICE = C(1)*PRICE(-1) + C(2)*DAC(-1) + C(3)*DAO(-1) + C(4)*DBEARS(-1) + C(5)*DBULLS(-1) + C(6)*CCI(-1) + C(7)*DFRAMA(-1) + C(8)*DMACDM(-1)
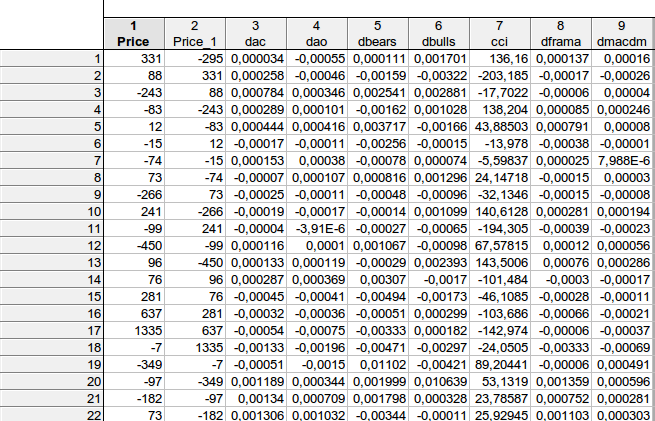
В общем, приблизительно получил похожий результат - отвергнуть нулевую гипотезу о равенстве рассматриваемых коэффициентов нулю никак нельзя...
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Опубликована статья Использование дискриминантного анализа для построения торговых систем:
Автор: ArtemGaleev