Денис, у меня к статье такое замечание.
По поводу теории - вопросов нет, все изложено достаточно подробно.
Что касается практики, обращу ваше внимание на рисунки, где у вас показаны эмпирические гистограммы, особенно, рисунок 2. Дело в том, что вы при анализе допустили две весьма существенные неточности.
Во-первых, вы задали скрипту, генерирующему гистограммы, слишком маленькое количество классов - всего 9, что само по себе уже долбанет по мощности критерия Пирсона и делает его применение малоэффективным. На будущее, берите для верности 200-300 классов, естественно если объем выборки позволяет (а он позволяет), не ошибетесь. Если бы вы сделали именно так, то смогли бы убедиться, что тест на логнормальное распределение дал бы отрицательный результат, равно как и тест доходностей на гиперсеканс. Кстати, очень просто можно убедиться в том, что два таких распределения не могут одновременно представлять некую величину и ее модуль, для этого достаточно взять "половинку" гиперсеканса и произвести ее свертку с самой собой (аналог взятия модуля от случайной величины): логнормального при этом точно не получится.
Вторая неточность в том, что вы не воспользовались априорным знанием о том, что вершина (она же матожидание) распределения доходностей должна находиться точно в точке 0 (иначе мы все бы давно были миллиардерами). Именно поэтому гистограмма на рисунке 2 выглядит смещенной вправо, хотя не должна бы. Опять же, учет этого момента при построении гистограммы сделал бы тесты заведомо достовернее.
П.С. не шатко, не валко пишу статью по основам моделирования, отсюда такой живой интерес. За вашу статью спасибо, она в тему. С уважением.
...Во-первых, вы задали скрипту, генерирующему гистограммы, слишком маленькое количество классов - всего 9, что само по себе уже долбанет по мощности критерия Пирсона и делает его применение малоэффективным. На будущее, берите для верности 200-300 классов, естественно если объем выборки позволяет (а он позволяет), не ошибетесь. Если бы вы сделали именно так, то смогли бы убедиться, что тест на логнормальное распределение дал бы отрицательный результат, равно как и тест доходностей на гиперсеканс. Кстати, очень просто можно убедиться в том, что два таких распределения не могут одновременно представлять некую величину и ее модуль, для этого достаточно взять "половинку" гиперсеканса и произвести ее свертку с самой собой (аналог взятия модуля от случайной величины): логнормального при этом точно не получится.
Уважаемый alsu, спасибо за мнение!
Давайте по порядку.
Количество классов задаётся не в добровольном порядке, а согласно некоторой формуле. У меня это формула Стёрджеса. Одно из самых популярных правил. Оно не идеальное, с этим согласен. Но тем не менее...
А вы берёте 200-300 классов согласно какому правилу?
Вторая неточность в том, что вы не воспользовались априорным знанием о том, что вершина (она же матожидание) распределения доходностей должна находиться точно в точке 0 (иначе мы все бы давно были миллиардерами). Именно поэтому гистограмма на рисунке 2 выглядит смещенной вправо, хотя не должна бы. Опять же, учет этого момента при построении гистограммы сделал бы тесты заведомо достовернее.
Я анализирую выборку по факту. Что имею, то и анализирую. А на каком основании вершина распределения доходностей должна находиться точно в точке 0? Может что-то недопонимаю...
А кроме того, если вы посмотрите, к какому распределению реализовывалась подгонка (а это было X~HS(-0.00, 1.00)), то несложно заметить, что первый параметр - параметр сдвига - равен именно 0. По факту он равен матожиданию.
Вот ещё html-отчёт по выборке станд. значений. Надеюсь, что рисунок более менее читаем. Правда он не идентичен тому, что в статье. Взял только что последние данные просто.
Как заметно, Mean =0. И самое подходящее - это Hyperbolic Secant distribution: X~HS(0.00, 1.00).
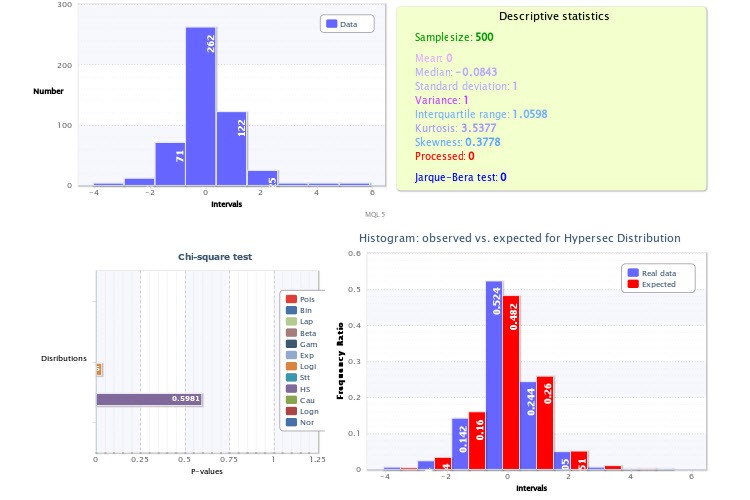
Точно, формула Стерджеса дала именно 9 классов, но это скорее повод задуматься об увеличении размера выборки (обращая формулу, вижу, что оно у вас в районе 256?).
Кроме того, эта формула хорошо работает только для генеральных совокупностей из нормального распределения (для которых она и была выведена) и, как считается, объеме выборки не более 200 значений. Можно воспользоваться альтернативными формулами - Диакониса, Скотта...
Вообще, знаете, Стерджес ведь так и не привел логического обоснования своей формулы - да, она основывается на аппросксимации нормального распределения биномиальным, ну и что? Каким образом это может повлиять на вопрос эффективности выбора количества классов? Критерий оптимальности-то автором определен никогда не был и сама формула написана наобум. Но дело в том, что долгое время подход Стерджеса был вообще единственным хоть как-то формализованным, и он на автомате (и, по моему мнению, совершенно бездумно!) был внесен во все статпакеты, что, кстати, немало раздражает именно потому, что эта формула практически всегда дает крайне заниженное число классов.
Еще раз повторюсь, есть альтернативные формулы, но именно наличие персонального компьютера, как ни парадоксально, дает возможность использовать в качестве прибора свою собственную голову, т.е. визуальный способ определения более-менее оптимального количества классов для данной конкретной выборки, когда, плавно изменяя этот показатель, мы добиваемся компромисса между гладкостью графика и разрешающей способностью гистограммы. Кстати, часто этот способ - вообще лучше и быстрее всяких формул.
Всегда всем говорю - прежде, чем подставлять числа в формулы, поинтересуйтесь, что она означает и как (и стоит ли) ее применять. Короче, я против применения формулы Стерджеса, считаю ее устаревшей и неадекватной)
По поводу среднего значения. Матожидание значений доходностей должно находиться в точке 0 потому, что если бы это было не так, мы бы могли тупо делать ставки всегда в одну сторону, соответствующую знаку этого МО, и гарантированно получать доход любого загодя заданного размера. Ну а вершина должна совпадать с МО чисто из соображений симметрии: левая половина графика должна быть зеркальным отображением правой (повышение курса и понижение вроде как статистически равноправны, и различий между ними быть не должно), а значит центр симметрии совпадает с центром.
Поскольку вы берете HS(0.00, 1.00), следовательно, должны центрировать и классы - т.е. нулевой класс должен включать значения показателя в некотором симметричном интервале (-x0;x0), иначе мы вносим в вычисления систематическую ошибку, связанную со сдвигом классов относительно нуля, и она же в конечном счете вкрадывается и в результат теста хи^2. У вас точка 0 - не в середине нулевого класса.
На самом деле, вопрос, как на дискретных данных сделать классы симметричными довольно таки нетривиален, и, опять же, хорошо бы решать его для каждой конкретной выборки индивидуально и очень аккуратно, иначе рискуем получит неадекватный результат еще и из-за неправильного выбора границ разбиения на классы.
alsu, вы затронули тему, которая хотя и не была предметом моей статьи, но является крайне интересной. По мере сил буду дальше исследовать этот вопрос.
Спасибо за конструктивную критику!
Мне импонирует ваше мнение по поводу применимости научных знаний в трейдинге.
Подскажите, пожалуйста, какую из предложенных в списке книг Вы порекомендуете человеку, который поверхность знаком с теорией вероятностей и мат. статистикой.
Денис, добрый день.
Мне импонирует ваше мнение по поводу применимости научных знаний в трейдинге.
Подскажите, пожалуйста, какую из предложенных в списке книг Вы порекомендуете человеку, который поверхность знаком с теорией вероятностей и мат. статистикой.
Спасибо за мнение!
Я думаю, что нужно искать что-то для новичков тогда, какую-то лит-ру. Главное, чтобы текст книги не отбивал желание читать её дальше :-))
Мне чем-то понравился Гайдышев, а чем-то Булашев...
Тут интересная ветка.
- rsdn.org
Вторая неточность в том, что вы не воспользовались априорным знанием о том, что вершина (она же матожидание) распределения доходностей должна находиться точно в точке 0 (иначе мы все бы давно были миллиардерами).
Вовсе нет. Смещение вершины распределения относительно 0 (рост/падение инструмента) вовсе не означает, что так будет и в будущем. Именно поэтому большинство трейдеров не миллиардеры, а не потому что.
С уважением.
...Смещение вершины распределения относительно 0 (рост/падение инструмента) вовсе не означает, что так будет и в будущем...
Согласен.
Вопрос к alsu. Вы имели в виду рыночную эффективность, рассуждая про нулевую точку?
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Опубликована статья Роль статистических распределений в работе трейдера:
Автор: Dennis Kirichenko