Вычислить расстояние между двумя параллельными линиями включая ! - страница 6
Вы упускаете торговые возможности:
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Регистрация
Вход
Вы принимаете политику сайта и условия использования
Если у вас нет учетной записи, зарегистрируйтесь
Да
к сожалению я не математик (Для этого достаточно знать школьный курс алгебры за 8-й класс. И математиком быть для этого вовсе необязательно.
Расстояние обозначено d -- посмотри, как оно вычисляется.
Почему хрень ? Почему дохлый ?
Да потому что, если буквально воспроизвести код, то получается ерунда, которая при этом на всех чартах будет разной.
Углы нельзя мерить в системе координат, которая постоянно изменяется. У Вас угол будет так же меняться.
Вообще, Вы бы сказали то, зачем Вам это надо, может все уже используют другое решение для Вашей задачи.
для понимания, о чём идёт речь :
..................................................................
..................................................................
На Ваших картинках везде известны все точки пересечения, но по факту у автора нет данных координат точек соприкосновения со второй линией. Из картинок не очевидно, как Вы её нашли.
Вообще, Вы бы сказали то, зачем Вам это надо, может все уже используют другое решение для Вашей задачи.
Мне нужно знать разницу между двумя параллельными линиями ...
Красная линия - расстояние между линиями
пока это теория - http://www.cleverstudents.ru/line_and_plane/distance_between_parallel_lines.html а как же на практике такое сделать ?На Ваших картинках везде известны все точки пересечения, но по факту у автора нет данных координат точек соприкосновения со второй линией. Из картинок не очевидно, как Вы её нашли.
На картинках показан весь процесс решения поставленной задачи, в том числе и определение точек пересечения.
Олег avtomat 2018.03.31 04:30 #37
На картинках показан весь процесс решения поставленной задачи, в том числе и определение точек пересечения.
Олег avtomat 2018.03.31 04:30 #37
Внимательно смотрю рисунок (матлаб видимо?)
Выдвигаю гипотизу, мы видим две функции, где:
- "b" - это смещение по оси y,
- "a" это коэффициент наклона,
- "t" - это координата по оси "x"
- "z(t)" - новая функция, описывающая перпендикуляр
верно?
Смотрю дальше и не могу сообращить, следующие выражения показывают что - там где стрелочки и надпись "solve"?
Дальше возникает "r" (сторона треухольника?) - что это такое и что подразумевает формула словами - степень?
Дальше уже находите d, вроде как по всем известной формуле...
Внимательно смотрю рисунок (матлаб видимо?)
Выдвигаю гипотизу, мы видим две функции, где:
- "b" - это смещение по оси y,
- "a" это коэффициент наклона,
- "t" - это координата по оси "x"
- "z(t)" - новая функция, описывающая перпендикуляр
верно?
Смотрю дальше и не могу сообращить, следующие выражения показывают что - там где стрелочки и надпись "solve"?
Дальше возникает "r" (сторона треухольника?) - что это такое и что подразумевает формула словами - степень?
Дальше уже находите d, вроде как по всем известной формуле...
маткад
верно
"solve" = "решать" -- поиск точки пересечения линии с перпендикуляром, т.е. поиск значения t, при котором y(t)=z(t)
подставляем найденное t и определяем r=y(t) при этом конкретном t
таким образом, получаем координаты точки (t;r) пересечения для первой линии
для второй линии проделываем аналогичные действия
в результате получаем две точки, расстояние между которыми надо определить
определяем d по указанной формуле
маткад
верно
"solve" = "решать" -- поиск точки пересечения линии с перпендикуляром, т.е. поиск значения t, при котором y(t)=z(t)
Не торопитесь, решать значит, ага, а как решать не ясно. Я так понимаю через систему уравнений?
Не торопитесь, решать значит, ага, а как решать не ясно. Я так понимаю через систему уравнений?
любым удобным способом
можно численно, с приемлемой погрешностью -- большой роли это не играет
Но в данном случае всё очень просто решается аналитически.
напомню, что к заданным двум параллельным линиям можно провести бесконечное множество перпендикуляров, а для определения расстояния можно использовать любой из них
в частности, это тоже перпендикуляр к заданным линиям :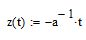
приравнивая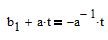
найдём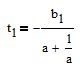
подставим это значение в уравнение линии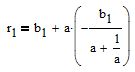
получим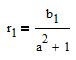
Первая точка (t1;r1) найдена. Вторая определяется аналогично.
Как видно, ничего сложного нет. Надо только немножечко подумать.