Вы упускаете торговые возможности:
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Регистрация
Вход
Вы принимаете политику сайта и условия использования
Если у вас нет учетной записи, зарегистрируйтесь
Может кто подскажет, какие существуют распределения с очень большим эксцессом, подобные до Лапласа, симметричные?
Любые существуют. Задавайте условия, вычисляйте параметры и распределяйте.
Будет распределение Novaja.
Так нет этой средней на форексе, то бишь постоянного мат ожидания. То есть возвращаться не к чему изначально... Можно возвращаться к машке как средней но тоже не факт что поможет...
Соответственно и отклонение от среднего это тоже фикция...
вы же тут все статистику на 5 знаете, в отличии от меня...
среднюю надо строить так, чтобы к ней цена всё-таки возвращалась
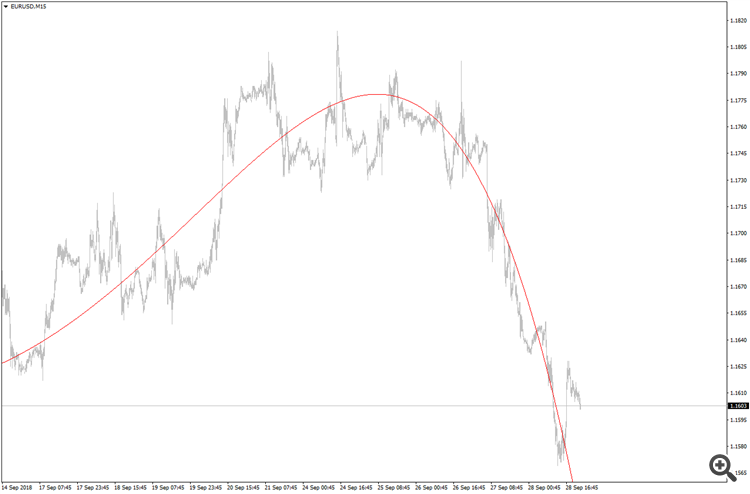
в экселе эта фича называется "полиноминальная линия тренда"вы же тут все статистику на 5 знаете, в отличии от меня...
среднюю надо строить так, чтобы к ней цена всё-таки возвращалась
в экселе эта фича называется "полиноминальная линия тренда"Неплохо. Круто, я бы даже сказал.
Неплохо. Круто, я бы даже сказал.
вы же тут все статистику на 5 знаете, в отличии от меня...
среднюю надо строить так, чтобы к ней цена всё-таки возвращалась
в экселе эта фича называется "полиноминальная линия тренда"
Эта фича использует будущие цены. Поэтому цена к ней и возвращается.
Ну ок, рынок фрактален. Посчитали Хёрста. Что дальше? Как это поможет прогнозировать?
Не об этом же идёт речь. Старайтесь всё же следить за ходом мысли, на какое высказывание и почему дан тот или иной ответ. И не выхватывайте из контекста, теряя при этом смысл, а то и вообще переворачивая всё с ног на голову.
Однако ж поясню, чтобы не было разночтений:
Речь о том, что А_К, не зная предмета, делает "удивительные" заявления, и ещё более "удивительные" выводы.
Форум по трейдингу, автоматическим торговым системам и тестированию торговых стратегий
От теории к практике
Alexander_K2:
Теперь вот какую вещь надо сказать.
Смотрю я на распределения приращений и как они меняют свои стат.моменты в зависимости от интервалов считывания котировок и понимаю, что рыночные цены НЕ обладают свойством самоподобия. Это свойство присуще исключительно процессам с устойчивыми, бесконечно делимыми (к примеру, нормальными) распределениями приращений - таким как броуновское движение. На рынке этого не наблюдается.
Очевидно, Мандельброт и его подельники, не шаря в физике (а еще хуже - шаря, но тщательно это скрывая), специально ввели в заблуждение страждущих, чтобы те поскорее переходили на скальпинг на тиковых данных и мелких таймфреймах и, сливая свои депозиты, пополняли их бездонные карманы.
Вот так-то!
Олег avtomat, 2018.09.29 02:55
ты уже и теорию заговора сюда приплёл... очередная чушь.
Ознакомься с предметом:
http://inis.jinr.ru/sl/vol2/Physics/Динамические%20системы%20и%20Хаос/Федер%20Е.,%20Фракталы,%201991.pdf
Эта фича использует будущие цены. Поэтому цена к ней и возвращается.
спасибо, не знал
только интересно - откуда они у неё?
Не об этом же идёт речь. Старайтесь всё же следить за ходом мысли, на какое высказывание и почему дан тот или иной ответ. И не выхватывайте из контекста, теряя при этом смысл, а то и вообще переворачивая всё с ног на голову.
Однако ж поясню, чтобы не было разночтений:
Речь о том, что А_К, не зная предмета, делает "удивительные" заявления, и ещё более "удивительные" выводы.
Вы тоже не сильны следить за контекстом. Я не про А_К, я про книжку, на которую вы сослались как на азбуку трейдера.
спасибо, не знал
только интересно - откуда они у неё?
Ну как откуда. Возьмите на этой полиномиальной линии любую точку t.
Для вычисления положения этой точки использованы цены как до нее (от 0 до t) так и после нее (от t до правого конца графика).
Не заглядывает в будущее только самая последняя точка полинома, на правом конце графика. Но к этой точке и цена возвращаться не будет.