Влияние спреда на прибыль или "На каком таймфрейме выгоднее всего торговать?" - страница 3
Вы упускаете торговые возможности:
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Регистрация
Вход
Вы принимаете политику сайта и условия использования
Если у вас нет учетной записи, зарегистрируйтесь
Кстати, интересно обратить внимание, что для ряда инструментов существуют параметры ТС, при которых торговля на самых младших таймфреймах заведомо невыгодна, т.е. даже максимальная потенциальная прибыль оказывается меньше нуля. Конечно, это верно только если ограничения задачи выполняются очень жестко (например, ТС, совершающая сделки строго на открытии каждого бара).
Кстати, интересно обратить внимание, что для ряда инструментов существуют параметры ТС, при которых торговля на самых младших таймфреймах заведомо невыгодна, т.е. даже максимальная потенциальная прибыль оказывается меньше нуля. Конечно, это верно только если ограничения задачи выполняются очень жестко (например, ТС, совершающая сделки строго на открытии каждого бара).
ну отношение волы к спреду важный показатель для торговли инструмента. Особенно на коротких периодах удержания позы. Этот показатель существенно меняется в течении суток. Правда в наиболее интересные моменты спреды обычно расширяются :)
Говорили, но я не поверил и измерил сам))) Зависимость действительно очень близкая к указанной, но к решению задачи это не имеет отношения, разве что захочется тот же результат получить аналитически..
Вот картинко оптимизации одной внутридневной системы.
По оси х - время удержания позиции в часах
Ну и ответ на вопрос топикстартера "на каком ТФ выгоднее торговать":
Видно, что при прочих равных условиях, tOpt пропорционален квадрату спреда.
Максимальная доходность пропорциональна следующему выражению: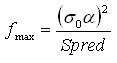
и выгодно юзать инструменты с большей волатильностью, чем с меньшим спредом (при прочих равных условиях).
Видно, что при прочих равных условиях, tOpt пропорционален квадрату спреда.
подтвердилось)
Выводы интересные и в целом подтверждают интуитивные наблюдения, но с практической точки зрения едва ли могут пригодится. Слабым моментом здесь является гипотеза статистической фрактальности, которую конечно необходимо принять для исследования этой функции. Как я понимаю, оптимальное t здесь является неким теоретическим пределом эффективности системы, т.е. не стоит использовать ТС на режимах меньше этого самого оптимального t (в этом наверное и заключается практическая значимость проведенного исследования).
Автору респект.
Слабым моментом здесь является гипотеза статистической фрактальности, которую конечно необходимо принять для исследования этой функции.
Интересно, но я как-то полагал, что это вполне себе сильное допущение. По крайней мере, опровержений я до сих пор не встречал, а вот подтверждений море
Автору респект.
Интересно, но я как-то полагал, что это вполне себе сильное допущение. По крайней мере, опровержений я до сих пор не встречал, а вот подтверждений море.
Возможно я и не прав, но даже "на глаз" разные таймфреймы весьма сильно отличаются друг от друга (прошу не пинять меня из-за употребления слова "на глаз"). Вот простая задача, напечатайте десять неподписанных произвольных графиков разных таймфреймов одного и того же инструмента. Попробуйте на глаз определить их таймфреймы. Уверен что процент верных ответов будет гораздо выше случайного попадания.
Еще как я понимаю, при допущении высокой степени фрактальности ТС должны вести себя одинаково не зависимо от ТФ. А вот это их свойство очень сомнительно, хотя мною целенаправленно и не исследовалось (а можно было бы этим заняться).
З.Ы. вот тут подумалось, что если учесть что на старших таймфреймах волатильность как и МО непропорциональна младшим таймфреймам, то соответственно нам и будут казаться графики более пологими и гладкими. Поэтому первое мое предположение некорректно.
Но вот второе остается в силе, надо исследовать этот вопрос.
Переделал скрипт под пятёрку. Притом добавил второй ряд данных -
(1)=abs(close[i]-close[i+1]) // как и было
(2)=max(abs(hi[i]-lo[i+1]),abs(lo[i]-hi[i+1]))
- т.е. увеличил теоретический выигрыш до максимального
Кто хочет может побаловать. Результаты выложу завтра (чего-то Excel тормозит сцуко), заодно ещё добавлю возможный в пятёрке расчёт по историческому плавающему спреду.
// кто будет играться - поставьте "макс. баров в окне" в терминале 1000000 баров. или подправьте скрипт, он сейчас 900000 баров на вход заглатывает. задано константой
Возможно я и не прав, но даже "на глаз" разные таймфреймы весьма сильно отличаются друг от друга (прошу не пинять меня из-за употребления слова "на глаз"). Вот простая задача, напечатайте десять неподписанных произвольных графиков разных таймфреймов одного и того же инструмента. Попробуйте на глаз определить их таймфреймы. Уверен что процент верных ответов будет гораздо выше случайного попадания.
Еще как я понимаю, при допущении высокой степени фрактальности ТС должны вести себя одинаково не зависимо от ТФ. А вот это их свойство очень сомнительно, хотя мною целенаправленно и не исследовалось (а можно было бы этим заняться).
З.Ы. вот тут подумалось, что если учесть что на старших таймфреймах волатильность как и МО непропорциональна младшим таймфреймам, то соответственно нам и будут казаться графики более пологими и гладкими. Поэтому первое мое предположение некорректно.
Но вот второе остается в силе, надо исследовать этот вопрос.
Что касается определения на глаз - да, я раньше тоже придерживался этого мнения. Ровно до тех пор, пока не появился пятизнак, т.е ошибка квантования уменьшилась в 10 раз - как-то сразу обратил внимание, что определить ТФ на глаз стало практически невозможно, если не смотреть на шкалу цен. Я потом даже действительно попробовал по-честному поугадывать, и ничего не вышло, как не выходит и сейчас.
Если не лень, можно набрать фокус-группу и провести исследование - человеческий моск хорошая нейросеть:), и наверняка зацепится за какие-то отличия, если они есть. Это было бы очень полезным делом.
Если касаться статхарактеристик, то я это дело исследовал достаточно много, и не нашел отличий на масштабах от 30 секунд до 24 часов (на большие ТФ данных маловато). Не знаю, может кто-то другой найдет что-то существенное. По моим данным, статистически идентичны: а) одномерная плотность распределения первых разностей (returns) б) уловная плотность распределения соседних returns в) автокорреляции соседних и г) функционал масштабирования (он близок в пределах 99% интервала к sqrt(TF)+const. для всех таймфреймов).
Конечно, если все же станет известно, что фрактальность где-то нарушается, буду рад об этом узнать, т.к. это потенциальный источник денег)))