Даю её вот такое уравнение
5-3(1-exp(-2*e*t/0.7))=2+3*(1-exp(-2*e*t/0.5))
![]()
![]()
![]()
Пишет что решения нет. :-)
Просто так, как квадратное, ты его не решишь, т.к. замена z=exp(-t) приводит его к уравнению по z, похожему на полиномиальное, но не полиномиальному.
Можно найти приближенное численными методами - или какое-нибудь аналитическое, разложив его, скажем, в ряд по коэффициентам. Общее уравнение - вида
А*z^alpha + B*z^beta = gamma.
Вообще похоже мне надо еще подумать - как оказалось уравнение составлено не верно. В частности "P" с левой и правой части не равны, и это на самом деле и было очевидно с самомго начала, но видимо уже зарешался.
Продолжаем решать уравнения :-)
Никто сходу не предложит метод по-проще для оценки параметров a и b для известных y(i) и x(i) ?
y(i) = (a + x(i))^b
=> log (y(i)) = b * log (a + x(i))
Если бы была одна, то всё решилось бы банальной линейной регрессией. Тут надо что-то небанальное. У меня есть одно решение, но там черт ногу сломит. Есть надежда, что должен быть метод попроще. Как вариант, можно просто тупой перебор с целью уменьшения суммы квадратов отклонений. Но хочется чего-то более изящного, но и не слишком извращенного.
Если нужно общее решение в зависимости от коэффициентов, то придется серьезно напрячься. Оно не будет элементарным, это точно.
Если же нужно частное решение при заданных числовых параметрах, то его можно найти любым подходящим числовым методом с приемлемой точностью.
Я решил, получилось очень длинно для упрошения, ( сказать что лень даже форумулу итоговую тут писать это ничего не сказат :-) ) но как ни странно очень кратко по результату. Ответ приводить не буду - это "военная тайна".
Но вообще согласитесь до чего прогресс дошел - ладно в маткаде есть симвальные вычисления ( это решатель уравнений и упрощатель, ну в 12-ом по крайне мере есть точно ) но уже просто онлайн это можно делать. Да и программа Algebrator стоит 39 баксов.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Пожалуйста помогите / подскажите решение помоему простого уравнения.

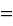
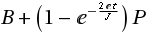
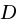
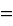
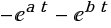 ну если просто все константы обьединить в 'D', а вместо
ну если просто все константы обьединить в 'D', а вместо 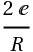 поставить 'a' и соответственно вместо
поставить 'a' и соответственно вместо 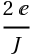 поставить 'b'
поставить 'b'
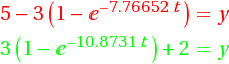
A-P(1-exp(-2*e*t/R))=B+P*(1-exp(-2*e*t/J))
Я пробовал и что-то похоже уже просто зациклился, а все вроде примитивно... :-)
Нашел даже в сети замечательный "рeшатель" - https://www.mql5.com/go?link=https://quickmath.com/webMathematica3/quickmath/page.jsp?s1=equations&s2=solve&s3=advanced просто суппер!
Но в итоге у меня получается только,что-то вида =>
Система пишет что решения нет! Но !!
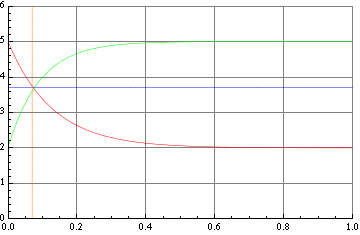
Если вместо констант поставить A=5; P=3;R=0.7;J=0.5;B=3;
То очевидно что есть решение -
На том-же замечательном сайте есть Plot ( рисование) выше картинка как раз оттуда.
t ~ 3.7 и y~0.07