(1) H(z) = a/(a+16*sin(w/2)^4)
(2) H(z) = a/(a+[z^(1/2)-z^(-1/2)]^4)
Во втором равенстве возможно утерян коэффициент 16, должно быть так:
H(z) = a/(a+16[z^(1/2)-z^(-1/2)]^4)
(1) H(z) = a/(a+16*sin(w/2)^4)
(2) H(z) = a/(a+[z^(1/2)-z^(-1/2)]^4)
Во втором равенстве возможно утерян коэффициент 16, должно быть так:
H(z) = a/(a+16[z^(1/2)-z^(-1/2)]^4)
Спасибо, но коеффициент 16 не утерян, а сократился.
(1) H(z) = a/(a+16*sin(w/2)^4)
sin(w/2) = [z^(1/2)-z^(-1/2)]/(2*j)
sin(w/2)^4 = [z^(1/2)-z^(-1/2)]^4/16
(2) H(z) = a/(a+16*[(z^(1/2)-z^(-1/2))/2]^4/16) = a/(a+[(z^(1/2)-z^(-1/2))/2]^4)
За свою жизнь я поистроил немало цифровых фильтров, а с таким случаем ещё не сталкивался. Похоже я за деревьями не вижу леса. Допускаю где-то элементарную ошибку, но где?
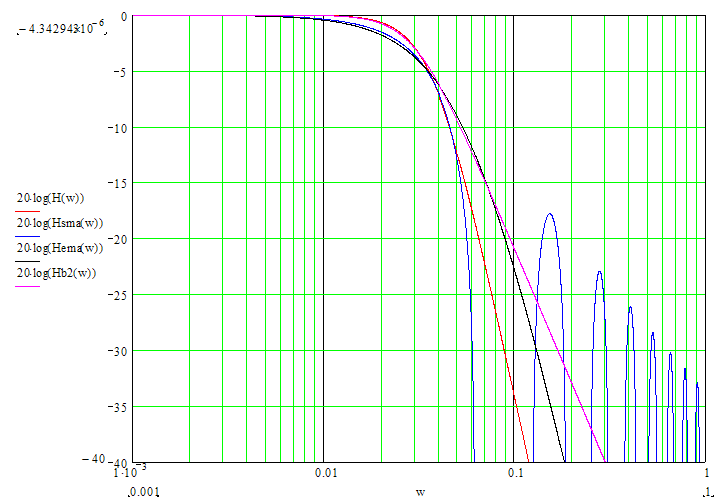
Кстати, вот графики разных передаточных функций (H - функция, обсуждаемяя здесь, Hsma - простой мув, Hema - показательный мув, Hb2 - фильтр Баттерворта 2-го порядка)
Возможно, ошибка в этом равенстве:
(3) H(z) = a*z^(-2)/[1-4*z^(-1)+(6+a)*z^(-2)-4*z^(-3)+z^(-4)]
Правильно так:
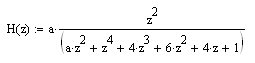
Возможно, ошибка в этом равенстве:
(3) H(z) = a*z^(-2)/[1-4*z^(-1)+(6+a)*z^(-2)-4*z^(-3)+z^(-4)]
Правильно так:
Почему меня привлекает этот мув? Прочитал две инетерсные ветки здесь: одну про использование НЧ фильтров для предскзания будущего, другую о фильтре Ходрика-Прескота. Отличительное качество фильтра Ходрика-Прескота в том что он не имеет задержки, т.е. заглядывает в будущее. Некоторые жаловались: а зачем такой фильтр, который перерисовается. Мне стало очень интересно. Если фильтр Ходрика-Прескота заглядывает в будущее, то какие будущие значения он предполагает? Чтобы ответить на этот вопрос, нужно найти формулу для этого фильтра, включающую будущие значения. Но фильтр расчитывается путем минизации целевой функции, т.е. подгонкой. Значит задача становится найти фильтр, похожий на фильтр Ходрика-Прескота, но значения которого расчитываются напрямую используя прошлые значения цены и самого фильтра-близнеца (casual filter). Такой фильтр-близнец должен иметь задержку как и все другие casual НЧ фильтры. Если сдвинуть значения этого фильтра-близнеца в прошлое на количество баров равному задержке Тзад, то значения фильтра-близнеца должны совпасть со значениями фильтра Ходрика-Прескота. Значения фильтра Ходрика-Прескота за самые последние Тзад-1 бары, за которые отсутствуют значения сдвинутого фильтра близнеца, смотрят в будущее. Прогноз будущего осуществляется таким образом. Берем значение фильтра Прескота на Тзад-1 бар и предполагаем что это значение принадлежит фильтру близнецу с неизвестной будущей ценой Close[-1]. Зная формулу фильтра близнеца и его будущее значение, предсказанное фильтром Ходрика-Прекота, расчитываем Close[-1]. Переходим к Тзад-2 и расчитываем таким же образом будущее значение Close[-2], и т.д. Проблема здесь найти филтьр-близнец для фильтра Ходрика-Прескота. Я пробовал SMA. Но частотная функция SMA не сильно похожа на частотную функцию HP фильтра и поэтому их сглаженные значения отличаются. В конце концов, я разыскал частотную функцию HP фильтра (функция, которую мы здесь обсуждаем) и решил вывести дифф уравнения напрямую из неё. Но они дают нестабильность. Мой следующий шаг - использовать фильтр Баттерворта 4-го порядка, который наиболее близко совпадает с фильтром Ходрика-Прекота.
Кстати, ваша формула для H(z) не включает минус перед некоторыми членами в знаменателе, а он там должен быть.
Отличительное качество фильтра Ходрика-Прескота в том что он не имеет задержки, т.е. заглядывает в будущее. Некоторые жаловались: а зачем такой фильтр, который перерисовается. Мне стало очень интересно.
По-человечески написанный ХП не заглядывает в будущее и имеет ФЗ (так устроен этот мир). Вобще, просто поразительно, насколько неустранима в человеке вера в волшебство! Вы, gpwr, на полном серьёзе хотите ловкостью рук (засунуть фильтр в один рукав и высунуть его через другой) получить данные из будущего? Бог в помощь.
Меня во всём этом другое заинтересовало. ХП интересен тем, что является трендследящим мувом. Это следует из минимизации функционала при выводе его рекурентной формулы. Выполняется требование равенства нулю суммы квадратов второй производной. Действительно, НП при наличии тренда прилипает к нему без запаздывания. Я тут копался в статье Булашёва посвящённой оптимизации цифровых фильтров и нашёл описание ФНЧ МЕМА, он интересен тем, что помимо требования минимизации второй производной, одновременно требуется минимизация первой, т.е. этот мув ещё и самый гладкий из всех трендследящих! Вот его рекурентное выражение:
![]() , где w - принадлежит промежутку 0...1
, где w - принадлежит промежутку 0...1
Так вот, если построить торговые каналы на основе этого мува, то они выглядят весьма привлекательно:
Как пишет сам Булашёв:

Может имеет смысл посмотреть на это внимательнее? Код индикатора приклеен ниже.
gpwr, я в цифровых фильтрах ничего не смыслю (а надо бы, наверно; в студенчестве пытались меня к ним приучить), но с Neutron'ом согласен. Однако очень рад, что с математикой Вы "совсем не на Вы". Не слишком основательной подготовки в статистике будет достаточно, чтобы избавиться от одержимости сверхидеей гладкого ФНЧ с нулевой ФЗ. Попробуйте посмотреть на поток разностей соседних значений любого ФНЧ как на случайный процесс.
P.S. У меня к Вам предложение: Jurik построил великолепный цифровой ФНЧ. Вылеченная версия лежит здесь. Может, посмотрите на код и на сайт автора попристальнее и скажете что-нибудь? По отзывам, очень близок к настоящему, который куплен у автора. Но и по отношению к нему у меня стойкое подозрение, что он перерисовывается - почти незаметно, но все же в будущее заглядывает. Собираюсь проверить эту гипотезу в ближайшем будущем.
... Я тут копался в статье Булашёва посвящённой оптимизации цифровых фильтров и нашёл описание ФНЧ МЕМА, он интересен тем, что помимо требования минимизации второй производной, одновременно требуется минимизация первой, т.е. этот мув ещё и самый гладкий из всех трендследящих! Вот его рекурентное выражение
Если не затруднит. Уточни.
1.Почему в качестве X(k), выбрано Open(i)
2. Что это за формула вычисления sigma, откуда она
3. w={0…1} в индикаторе =10, это из-за вот этой лишней строчки w=1./w;
4. У Булышева вроде бы несколько трудов. Можно название и номер страницы.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
 испр.
испр.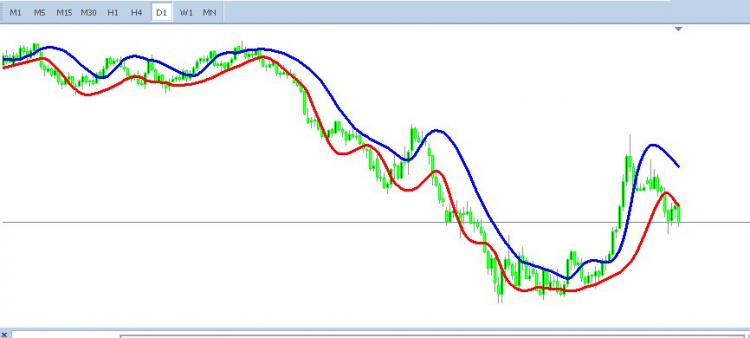
Уже два дня маюсь над, казалось бы, простым фильтром. Итак, задаю необходимую функцию передачи в z-domain:
(1) H(z) = a/(a+16*sin(w/2)^4)
где 0<а<1 и z=exp(j*w). Вроде, судя по этой функции, коеффициент передачи всегда меньше 1 кроме нулевой частоты, при которой H(z)=1. Поэтому ожидаю что фильтр будет стабильным. Заменяю sin(w/2) = [exp(j*w/2)-exp(-j*w/2)]/(2*j) = [z^(1/2)-z^(-1/2)]/(2*j). Подставляю в (1) и получаю
(2) H(z) = a/(a+[z^(1/2)-z^(-1/2)]^4)
После простых преобразований, прихожу к
(3) H(z) = a*z^(-2)/[1-4*z^(-1)+(6+a)*z^(-2)-4*z^(-3)+z^(-4)] = Y(z)/X(z)
Перехожу к дифф. уравнению:
Y(z)*[1-4*z^(-1)+(6+a)*z^(-2)-4*z^(-3)+z^(-4)] = X(z)*a*z^(-2)
y[0]-4*y[1]+(6+a)*y[2]-4*y[3]+y[4] = a*x[2]
(3) y[0]=4*y[1]-(6+a)*y[2]+4*y[3]-y[4]+a*x[2]
Пишу индюк для построения выхода этого фильтра. Получаю нестабильность. Никак не пойму почему. Пожалуйста разьясните. Индюк прикреплён.