Ещё одын вопрос о перцептроне. Отвечаем!

Новый комментарий
 

Несколько лет назад Юрий Решетов написал статью о нейросети и показал её простейший пример на одном перцептроне.

Там был такой код:

double perceptron() 
  {
   double w1 = x1 - 100.0;
   double w2 = x2 - 100.0;
   double w3 = x3 - 100.0;
   double w4 = x4 - 100.0;
   double a1 = iAC(Symbol(), 0, 0);
   double a2 = iAC(Symbol(), 0, 7);
   double a3 = iAC(Symbol(), 0, 14);
   double a4 = iAC(Symbol(), 0, 21);
   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4);
  }

Вот рассуждая о принципах работы нейросети я задался вопросом: почему 4 входа у нейрона?

Один вход - даёт нейрону сведения о текущем расположении.

Два входа - дают информация о скорости изменения цены.

Три входа - передают данные о ускорении движения котировок.


Текущая цена, скорость, ускорение - вполне достаточно информации для обработки нейросетью.

Зачем тогда четвёртый вход? Какую информацию можно получить от четырёх точек графика?


Кто-нибудь занимался определением (практическим или логическим) оптимального количества входов в нейрон?

Если есть такие - поделитесь инфой. Заранее спасибо ;)

 

Павел, новогодние празднества еще не начинались толком, а ты, похоже, уже недоперепил. Столько серьезнейших вопросов в одном сообщении - это уже слишком. Ты давай-ка поправляй здоровье, а через пару недель после НГ приступишь к НС с новой силой.

P.S. Вот подумал я еще слегка над четвертым входом: а время-то, время куда девать?!

 
meta-trader2007 писал(а) >>

Несколько лет назад Юрий Решетов написал статью о нейросети и показал её простейший пример на одном перцептроне.

Там был такой код:

Вот рассуждая о принципах работы нейросети я задался вопросом: почему 4 входа у нейрона?

Один вход - даёт нейрону сведения о текущем расположении.

Два входа - дают информация о скорости изменения цены.

Три входа - передают данные о ускорении движения котировок.

Текущая цена, скорость, ускорение - вполне достаточно информации для обработки нейросетью.

Зачем тогда четвёртый вход? Какую информацию можно получить от четырёх точек графика?

Кто-нибудь занимался определением (практическим или логическим) оптимального количества входов в нейрон?

Если есть такие - поделитесь инфой. Заранее спасибо ;)

Вообще-то, нелинейная траектория любого обьекта (в том числе и цены) описывается бесконечным множеством членов:

y=a0+a1*t+a2*t^2+a3*t^3+...

- разложение в ряд Тэйлора/МакКларена по времени t. Коэффициенты а0,а1... неизвестны но могут быть получены путём дифференцирования по времени:

a0=dy/dt |t=0

a1=d^2y/dt^2 |t=0 - скорость

a2=d^3y/dt^3/2 |t=0 - ускорение

...

Заметьте что эта модель траектории цены не учитавает память. То есть цена определяется текущими производными разного порядка. На самом деле, рынок обладает памятью. То есть сегодняшняя цена зависит от того где она была вчера, неделю назад, год назад и т.п. Чем дольше период, тем слабее память. Память моделируется путём введения временной зависимости для a0,a1,a2... То есть a0(t), a1(t), a2(t) ... Поэтому перцептрону необходимо подавать данные разной задержки чтобы определить эту временную зависимость коэффициентов и предсказать будущее.

 
gpwr писал(а) >>

Вообще-то, нелинейная траектория любого обьекта (в том числе и цены) описывается бесконечным множеством членов:

y=a0+a1*t+a2*t^2+a3*t^3+...

- разложение в ряд Тэйлора/МакКларена по времени t. Коэффициенты а0,а1... неизвестны но могут быть получены путём дифференцирования по времени:

О чём вы пишите?

Весь матаппарат дифференциального исчисления по определению применим к гладким, бесконечно-дифференцируемым функциям! Мы же имеем дело с временными рядами, которые при всём желании к гладким отнести нельзя, и не нужно пытаться их предварительно сгладить мувингом, а затем дифференцировать! Это сродни попытке Мюнхаузена вытащить самого себя из болота, во-преки здравому смыслу и третьему закону Ньютона. Не работает на ценовых рядах разложение в ряд Тейлора. Из-за нестационарности гармоник, не может работать и не работает фурье-анализ.

meta-trader2007 писал(а) >>

Текущая цена, скорость, ускорение - вполне достаточно информации для обработки нейросетью.

Зачем тогда четвёртый вход? Какую информацию можно получить от четырёх точек графика?

Кто-нибудь занимался определением (практическим или логическим) оптимального количества входов в нейрон?

Если есть такие - поделитесь инфой.

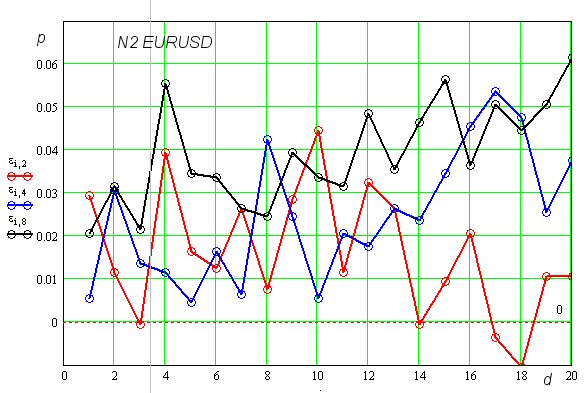
Обратите внимание на классическую фигуру ТА - Голова-плечи. Для обнаружения этого паттерна требуется 7 точек, соответственно, НС заточенная под это дело, должна иметь размерность входа как минимум 7. Далее, семейство паттернов, конечно, не ограничивается сверху по параметру звеньев. Можно НС поручить самой находить устойчивые фигуры произвольной сложности, соответственно и размерность входов НС должна быть произвольной. Например, на рис. приведены зависимости предсказательной способности двухслойного нелинейного персептрона как функции от размерности входа d (ось абсцисс) и числа нейронов в скрытом слое (цвет графика):

 
Neutron писал(а) >>

О чём вы пишите?

Весь матаппарат дифференциального исчисления по определению применим к гладким, бесконечно-дифференцируемым функциям! Мы же имеем дело с временными рядами, которые при всём желании к гладким отнести нельзя, и не нужно пытаться их предварительно сгладить мувингом, а затем дифференцировать! Это сродни попытке Мюнхаузена вытащить самого себя из болота, вопреки здравому смыслу и третьему закону физики. Не работает на ценовых рядах разложение в ряд Тейлора. Из-за нестационарности гармоник, не может работать и не работает фурье-анализ.

Сергей не все так однозначно. Исходная кривая цена - гладкая и вполне диферинцируема. Это метот оцифровки её никуда не годен. Оцифровку эту делает ДЦ (множество участников валютного рынка) и делает её не точно и плохо (нестационарно). Гармоники плывут в первую очередь потому что дельта t (период дискретизации или частота дискретизации), не константа. А в период гэпа вообще практически нет отсчетов.

Простейщий пример сегодняшний понедельник ГЭП GBPUSD. Как ты считаеш былбы он (гэп) если бы в суботу и воскресенье шли котировки. Так и с любым гэпом. Нехватает частоты дискретизации. Теорема Котельникова не выполняеться, отсюда и гэп.

 

Ну так и что нам с того, что где-то она гладкая? Эта информация не доступна в принципе - значит её нет, значит цена не является гладкой функцией. Или, Сергей, у тебя есть идеи?

Я, пока копался с однослойным персептроном, смог получить аналитические выражения для его весов для нелинейности заданной в специальной форме. Самое интересное, что это аналитическое выражение аналогично разложению в ряд, где число членов ряда оределяется размерностью входов НС. Так вот, это самое разложение работает не только для гладких функций, но и для ломаных на каждом отсчёте! Такое вот универсальное разложение получилось. И это представляет интерес! Что бы не быть голословным, вот аналитическое выражение такого разложения, полученное как решение для двух-входовой НС-ки:

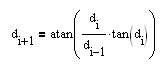где, d[i] - отсчёты в ряде первой разности исходного ВР. Т.е. прогнозируется приращение следующего отсчёта исходного ВР. Можете проверить, это выражение прогнозирует с лёгкостью и ряд типа sin(x) и ряды типа (-1)^n. Конечно, это выражение слишком слабо, для работы на рыночных ВР, но кто говорил, что нужно ограничится двумя входами?

 
Neutron >>:

///

что нужно ограничится двумя входами?

Скажите как наращивается данное выражение до 3 и более входов ?

 

Вы, наверное, решили, что если есть бык, то его неприменно нужно брать за рога!

Сначала подрастите бычка:-)

Новый комментарий