вопрос по матьематьике

Новый комментарий
 

не могу сообразить че добавить в формулу:

Result = MathLog ( ( A / B - 1 ) / SD +1 ) ;

А и Б - некие цены

СД - значение стандартного отклонения т е на два три порядка меньше чем А или Б


формула выдает правильный результат на котировках типа фондовых индексов с крупными числами

на котировках валютных пар для области отрицательных значений формула выдает ерунду


цель формулы объеденить две простых формулы которые по одиночки естесно работают без проблем:


Result = ( A - B  ) / SD ;

СД нужно для приведения к общему знаменателю на разных таймфреймах (масштабирование) но хочица еще иметь нелинейность..


Result = MathLog ( A / B ) ;

логарифм дает нелинейность но хочица иметь один масштаб на разных ТФ

 

вопрос по матьематьике

Ну, что за "матьематьике"? Правильно - мотьемотье-ё!

Попробуй так:

Result = MathLog ( 1+A / B) ; - нелинейность есть, нормировать не нужно и работает всегда.

 
Neutron >>:

Result = MathLog ( 1+A / B) ; - нелинейность есть, нормировать не нужно и работает всегда.

нужна симметричная нелинейность т е двухполярный сигнал осцилятора

 

Тогда так:

double th(double x)
{
if(MathAbs(x)<100.)S=(MathExp(x)-MathExp(-x))/(MathExp(x)+MathExp(-x));
else S=MathAbs(x)/x;
return(S);
}

х=A/B-1.;

Result=th(х);

Это формула для гиперболического тангенса. Всё симметрично и нелинейно!

Нужно, что бы А и В сидели на трубе (шутка), были одного порядка (принадлежали одному ТФ и одному инструменту). В противном случае, необходимо их нормировать по-отдельности, например на характерное значение цены по каждому инструменту и т.п.

 
Neutron >>:

Тогда так:

double th(double x)
{
if(MathAbs(x)<100.)S=(MathExp(x)-MathExp(-x))/(MathExp(x)+MathExp(-x));
else S=MathAbs(x)/x;
return(S);
}

х=A/B-1.;

Result=th(х) ;

Всё симметрично и нелинейно!

а общий знаменатель как?

попробывал заменить х=A/B-1 на х=(A-B)/SD получился меандр ))

 

sabluk, зачем тебе общий знаменатель для выражения A/B-1? Ты хочешь оперировать, неприменно, тремя переменными в одной формуле? Если А, В и SD меняются, то можно определиться так:

х=((A-B)/SD)/((A0-B0)/SD0), где A0, B0 и SD0 фиксированные значения переменных A, B и SD на како-то определённый момент времени (например, на 100 бар). Если SD всегда константа, то формула упрощается:

х=(A-B)/(A0-B0).

Поскольку в последнем выражении SD вобще нет (нафик она нужна), то проще пользоваться выражением:

х=A/B-1, если А и В сравнимы, то меандра не получится. Если отличаются более чем в 2-а раза, то их нужно нормировать:

х=(A/А0)/(В/В0)-1

 
Neutron >>:

sabluk, зачем тебе общий знаменатель для выражения A/B-1? 

без масштабирования советнег младшие ТФ не услышит

чувствую что мою формулу не сложно подправить но крыша уже отъехала

 
Выпей чего-нибудь:-)
 

Логарифм отрицаетльного числа существует. Получается комплексное число. MQL к сожалению не понимает SQRT(-1). Поэтому огромное количество алгоритмов не возможно реализовать, особенно связанных с фазой. И у тебя из-за этого все рушиться тоже.

sabluk

попробуй описать словестно что ты хочеш получить, может и придумаем тогда нормировку

 

я кажись понял свою ошибку

нада делать расчет отдельно для каждого полупериода чтобы симетрия была

при сильно малых значених логариф стремица к минус бесконечности


 
sabluk >>:

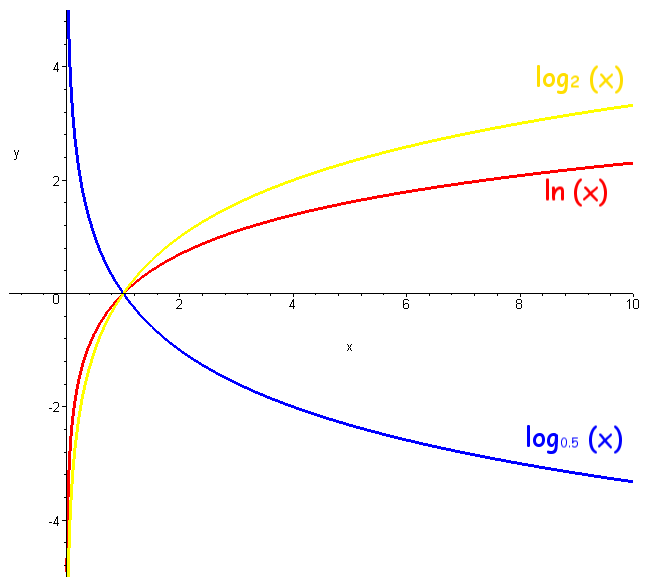
без масштабирования советнег младшие ТФ не услышит

чувствую что мою формулу не сложно подправить но крыша уже отъехала

Neutron прав. Если нужна нелинейность и четкое ограничение области значений, th(x) то что нужно.


Попробуй th((A - B)/SD).

Порог чувствительности(нелинейности) правда придется подбирать. Т.е. th(K*(A - B)/SD) Где K тот самый порог.

123
Новый комментарий