Показатель Херста - страница 45

Новый комментарий
 

Появилась версия  R 3.0.0

Все надо переустанавливать, включая RStudio.

Кстати, знает ли кто-нить как избавиться об обязательности 4 окон. 

 

faa1947:  

Кстати, знает ли кто-нить как избавиться об обязательности 4 окон. 

Перетаскиванием вертикальной и горизонтальных границ можно скрывать не нужные окна.
 
WWer:
Перетаскиванием вертикальной и горизонтальных границ можно скрывать не нужные окна.
Действительно, спасибо
 

Кстате, если кого интересует:

Розтягиваем Ренко на графике в акурат по первому колену Зигзага от и до с подбором кирпича.

И на нулевом колене смотрим отставание или опережение начала Ренко относительно пика Зигзага.

Система настраивается типо фиб, но результат - кривулька в подвале от нулевого уровня.

 

Не так давно судьба свела с данной темой, и сразу возникло несколько вопросов. Уважаемые знатоки, не могли бы вы мне помочь найти ответы на эти вопросы? Не пинайте сильно, если какой-либо из вопросов на Ваш взгляд покажется глупым...

Итак:

1) Существует несколько способов нахождения показателя Херста. Какой из эти способов (на Ваш взгляд) лучший (дает более точную оценку показателя)? Если возможно, укажите ссылку на источник.

2) Данный показатель должен быть инвариантным относительно линейных преобразований? (Желательно развернутый ответ).

3) Если ряды коррелируют между собой, то что можно сказать о показателях Херста?

4) Имеется три ряда. Для каждого ряда посчитан показатель Херста. При сложении рядов, что можно сказать о показателе?

Заранее благодарен.

 

Может по использованию языка R завести отдельную ветку? Делиться опытом и результатами.

Конечно если есть заинтересованные.

Удачи

 

Снова вернулся к анализу этого нетривиального показателя. Долгое время меня смущал побочный коэффициент, получающийся при расчете величины Херста. По сути, Херст выражается через линейное уравнение в двойном логарифмическом масштабе, где на оси ординат (Y) откладывается пройденное ценой расстояние в отнормированном мастштабе, а на оси абсцисс (X) - характерный период (таймфрейм или горизонт). Это линейное уравнение есть аппроксимация точек, которые мы измерили опытным путем и нанесли на график. Формула уравнения проста и очевидна:

 

На некоторое время представим, что коэффициент  равен нулю и упростим формулу до 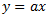. Значение  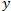здесь является расстоянием, пройденным ценой. Значение  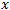- временным периодом. Очевидно, что при классическом броуновском движении цена проходит расстояние соответствующее квадратному корню из , где 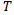 - время или период:

 

Это уравнение является частным случаем нашей формулы, при :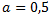

 

Этаже формула в двойном логарифмическом масштабе будет соответствовать собственно нашей линейной функции:

 

Где 0.5 - Коэффициент Херста.

Все эти расчеты тривиальны, однако в них пренебрегается неудобным коэффициентом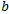 , который в реальности почти всегда значимое число. Как же понять этот коэффициент?  Мои математические размышления над природой этой зависимости привели к пониманию этого коэффициента. Ведь он появляется лишь тогда, когда мы аппроксимируем наши эмпирические точки линейной функцией. Для каждой конкретной точки всегда известен ее H. Коэффициента  у нее нет, т.к. для нее нет и общей аппроксимирующей функции. Рассмотрим простой пример, попробуем рассчитать H визуально для точек C и D R/S графика EURUSD:

 

Для точки С - это примерно 0.45, для точки D - 0.51. Т.к. обе точки практически идеально ложатся на аппроксимирующую прямую (y = 0,5304x - 0,0757 ) мы можем рассчитать точное значения H для этих точке аналитически. Для C:

 

Для D:


Выполнив обратное преобразование для D, для этой точки значение по Y равно 1.5155, а значение по X соответствует 3, тогда его H будет:

 

 

Результат расчета показывает, что точка C является антиперсистентной (H = 0,4547), а D - фактически броуновской (H = 0.5051). Оценка H для всего ряда становиться бессмысленной, т.к. на малых горизонтах ряд проявляет свою антитрендовость а на больших горизонтах - наоборот, стремиться к все более трендовым движениям. Это полностью согласовывается с эмпирическими наблюдениями за валютами. Каждый, кто торгует ими достаточно долго, видит, что на малых масштабах цены постоянно колебляться во флэте, а на больших масштабах, протяженностью год и более происходят крупные трендовые движения.

Коэффициент  - это вроде релятивисткой поправки в физике. Он образует взаимосвязь с H и определяет изменения характера рынка с увеличением масштаба. Если этот коэффициент близок к нулю, то рынок однороден в своем масштабе. Трендовость или антиперсистентность в нем примерно на одном и том же уровне не зависимо от масштаба. Если b существенная величина - он является доминирующим начальным условием. H - начинает больше доминировать с увеличением масштаба. Вот типы взаимосвязей H и :

  • H больше 0.5; b - отрицательное число. При такой комбинации на мелких мастштабах рынок антитрендовый, но с ростом временного периода начинают проявляться тренды. Таким поведением обладают валюты;
  • H больше 0.5; b - положительное число. Рынок однороден. На всех масштабах доминируют тренды. Если H существенная величина, а b наоборот не большое, - более сильные тренды чаще встречаются на больших временных горизонтах. Чем горизонт больше - тем тренды на нем сильнее. Наоборот, если H не значительно, а b наоборот большое, - более сильные тренды встречаются на малых мастштабах, с ростом периода тренды продолжают быть, но их сила и чистота падает.
  • H меньше 0.5; b - отрицательное число. Рынок антиперсистентен на всех масштабах. Если H значимая величина, а b нет, - более частые и чистые возвраты к среднему происходят на более крупных таймфреймах. На более мелких таймрфеймах цена более склонна к случайному блужданию. Если, наоборот, b значимая величина, а H нет - рынок более слонен к возврату на мелких таймрфемах, на более длительных рынок ближе к броуновскому движению, но все равно сохраняет свою антиперсистентность.
  • H меньше 0.5; b - положительное число. При такой комбинации на мелких масштабах рынок проявляет трендовость, но на более крупных мастшатбах становиться антитрендовым. По всей видимости таким поведением обладала нефть в период ее стоимости в районе 100$ за баррель.

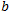Если b по своему модулю составляет существенную долю от H, то ограничиваться анализом только H нельзя. Рынок может проявлять два противоположенных свойства на разных временных мастштабах, например быть трендовым и антитрендовым одновременно.

Если H и b существенные величины и направлены в разные стороны (H - сильно больше 0.5, и - отрицателен или H сильно меньше 0.5 и b положителен) - на рынке наблюдается резкий переход от одного состояния к другому в зависимости от таймфрейма.  

 

Кто нибудь реализовывал формулу показателя времени указанную здесь:

http://cdn.scipeople.com/materials/2667/%D0%9F%D1%80%D0%B8%D0%BC%D0%B5%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5%20RS%20%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7%D0%B0%20%D0%BD%D0%B0%20%D1%84%D0%BE%D0%BD%D0%B4%D0%BE%D0%B2%D1%8B%D1%85%20%D1%80%D1%8B%D0%BD%D0%BA%D0%B0%D1%85%202.doc 

 5 странца

 
А индикатор показателя Херста есть для МТ4?
 
Кстати есть такой индикатор, индекс инвариантности. Который смотрит наклон линии регресии отвечая тем самым на вопрос есть тренд на рынке или нет. У меня всё руки не доходят, но хочб чтобы этот индект расчитывал не движение цены на рынке, а движение кривай баланса. Тем самым можно было бы видет происходит ли изменение баланса. Определяем в какую сторону, если вних, то зеркалим сигналы, если ввех, то повторяем. Мне кажется с таким помошником любую ТС можно вытянуть за уши.... Ну или зделать её более менее пригодной... Кто что скажет???
Файлы:
ivar.mq4  4 kb
1...383940414243444546
Новый комментарий