O fenômeno de São Petersburgo. Os paradoxos da teoria da probabilidade. - página 4
Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
Neste tópico, por favor, poste qualquer paradoxo da teoria da probabilidade que você possa encontrar.
Gabor Sekei. Paradoxos na teoria da probabilidade e na estatística matemática.
http://baguzin.ru/wp/wp-content/uploads/2016/05/Габор-Секей.-Парадоксы-в-теории-вероятностей-и-математической-статистике.pdf
Mas e se for de 0 a 5, ou 7, ou qualquer outro número? Você ainda tem que dividir por 32768,0. Ou existem opções?
É claro que é assim que deve ser:
Novaja:
В этой теме прошу выкладывать разные парадоксы теории вероятности, все, какие можно найти.
Enigmas matemáticos e diversão
Este livro do famoso popularizador científico americano M. Gardner tem muitos problemas e quebra-cabeças muito divertidos de diferentes ramos da matemática. Uma seleção bem sucedida de material, uma forma de apresentação bastante incomum e um humor sutil do autor trarão grande prazer a uma grande variedade de leitores - amantes da matemática que desejam passar seu tempo livre de forma útil.
Fonte:
Gardner M. 'Enigmas matemáticos e diversão'. \\Traduzido do inglês por Danilov Y.A., editado por Smorodinsky Y.A. - Moscou: Mir, 1971 - p.511
É claro que é assim que deve ser:
Sem utilizar o restante da divisão.
Sem utilizar o restante da divisão.
Acho que a "não aleatoriedade" só era realmente perceptível quando se definia "uniforme, estranho".
Se você usar um resto de divisão de números muito maiores que 2, é improvável que seja detectável.
A única maneira correta é usar números que sejam 2 para a potência de N em vez de 100, por exemplo 64, 128, 256...
Mas a redução de rand() para o dobro de 0 para 1 também é normal, porque é mais fácil entender um valor aleatório e mais preciso, embora um pouco mais lento. Mas acho que estamos falando de frações de um nanossegundo, embora possam ser nanossegundos, porque o processador precisa mudar de operações int para operações duplas(mistura FPU/ALU), e Renat disse uma vez que isto está longe de ser livre.
Neste tópico, por favor, poste qualquer paradoxo da teoria da probabilidade que você possa encontrar.
https://oschool.ru/files/studys/55df78bc740d76b70e8b4287/1443032585656.pdf
Você já viu pessoalmente um jogador fazer um palpite, mas não receber o prêmio? Eu nunca vi ninguém ganhar, exceto seus cúmplices.
Essas três cartas ou três dedais, de acordo com a teoria da probabilidade, são as vencedoras para os organizadores do jogo, e depois há o truque da mão.
Não há nenhum truque de mão ou teoria de improbabilidade. :) É tudo banal e simples. Eu sei disso em primeira mão. Foi nos anos 90 e o esquema foi-me descrito em grandes detalhes por um homem que estava envolvido nele. Agora as pessoas não se deixam enganar por isso; os golpistas operam principalmente on-line. Mas os princípios básicos permanecem os mesmos. Para atrair uma pessoa, tirar proveito de suas fraquezas e obter dinheiro dele, e então, sob qualquer pretexto, o dinheiro nunca é devolvido.
Os termos do jogo não estão totalmente descritos, como de costume.
É possível ganhar mais do que a sua aposta? Caso contrário, não vale a pena jogar.
Então, deve ser permitido ganhar do pote. Portanto, é suficiente fazer a aposta mínima, haverá uma vitória.
Talvez a condição seja que você possa jogar 1 vez, e aqui temos que decidir sobre a aposta, para que haja a máxima probabilidade de ganhar.
Como todos os "pradlocks" - de condições incompletas.
Solução:
Não há sequer uma questão de apostar. Aposta 1. Não faz mais sentido, a probabilidade de ganhar não depende do tamanho da aposta. Portanto, 1, só para começar o jogo.
Então, qual é o paradoxo? A partir do pressuposto de que você tem que fazer uma aposta maior para aumentar seus ganhos? Talvez seja isso.
O objetivo do jogo: para entrar no jogo é necessário um depósito e o jogo de moedas dura até que a primeira águia apareça (um jogo único), 1-doucat vence quando uma águia aparece na primeira rolada, se houver uma cauda e uma águia aparece na segunda rolada, a quantia vencedora é dobrada, e assim por diante até o infinito, até que uma águia apareça. Probabilidade de ganhar 1 ducado-0,5, 2-0,25, 4-0,125 etc., para que você possa ganhar o infinito, e jogar o infinito, se o pote for infinito.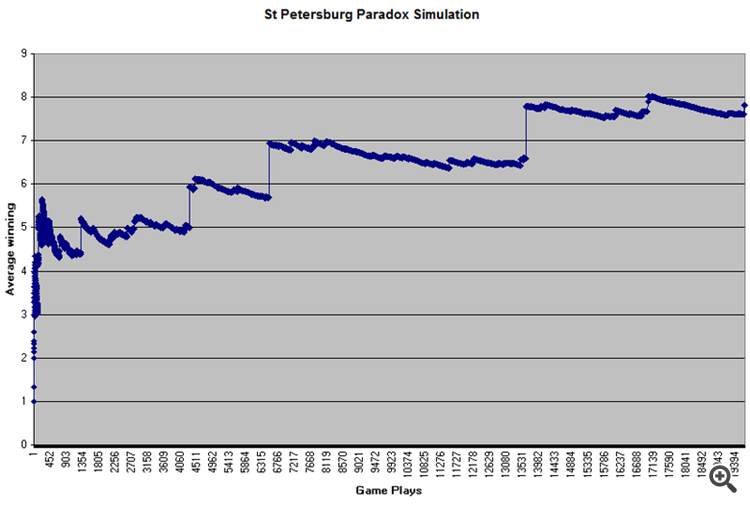
esta é uma função não-linear.
y=2^x.
e onde Y em uma função não linear tende se X tende ao infinito? correto, ao infinito.
Portanto, se o número de jogos = infinito, então a vitória média = infinito.
E o problema também é definido de tal forma que suas perdas são uma função linear (sempre 25 rublos cada), enquanto seus ganhos são uma função não linear.
É preciso traçar duas funções: primeiro o primeiro gráfico será mais alto que o segundo, depois eles trocarão de lugar.
Tudo depende do número de jogos.
Exatamente certo.
Mas e se precisarmos de 0 a 5, ou a 7 ou a qualquer outro número? Ainda temos que dividi-lo por 32768,0. Ou, existem variantes?
Se você não está satisfeito com a qualidade do CRT (por exemplo, com bits baixos), então você precisa passá-lo através do AES.
2. o restante da divisão pode ser tomado, mas somente se dividido por poderes de 2. Caso contrário, não importa quão bom seja o FGTS, o resultado não será nada como uma distribuição uniforme.
3) Com a divisão pelo dobro você pode ficar muito confuso com suas comparações :-) Na maioria dos casos você obtém uma produção pequena, mas enviesada.
para obter um número aleatório de 0 a 6 (um de 7):
- considere limite=RAND_MAX - (RAND_MAX%7) ; o múltiplo máximo de 7 na faixa 0...RAND_MAX
- usar o RDS até obter r<limit ; isto é, se "número aleatório" for maior que o limite, não podemos fazer nada com ele - tomamos
- resultado = r % 7 ou (para melhor ou pior) r * 7 / limite
de alguma forma :-) poderia estar errado +-1,