...
Há aqui uma montanha de paradoxos nos tervers e matstata não amados :-)
Por que a teoria da probabilidade e as estatísticas matemáticas de repente não são amadas aqui? Parece estar tudo bem com eles aqui. Mas com disparates baseados na teoria da probabilidade e em problemas de estatísticas matemáticas.
Quais são os paradoxos?
Einstein e o GTR/STO, isso geralmente é legal.
"há um enorme sapo voando na sua direção a 0,97C; você pode descobrir que é um sapo?"
Por que a teoria da probabilidade e as estatísticas matemáticas de repente não são amadas aqui? Eles parecem estar bem aqui. Mas existem problemas com tolices baseadas na teoria da probabilidade e nas estatísticas matemáticas.
Quais são os paradoxos?
É possível em MT4 testar automaticamente uma EA em ordem decrescente de tempo sendo testada? Por exemplo, de 2015.01.01 até 2015.12.31, próximo passo de 2015.01.02 até 2015.12.31 e assim por diante.
Eu resolvo este problema usando o otimizador:
//+------------------------------------------------------------------+ // Внешние переменные input bool CheckEvery_Day=false; input bool TestEachYearSeparately=false; input int DayOfYear_=1; input int Year_=2009; // Эксперт функция тик void OnTick(void) { if(CheckEvery_Day) { if(TestEachYearSeparately) if(Year()<Year_ || (Year()<=Year_ && DayOfYear()<DayOfYear_) || Year()>Year_) return; //тестировать каждый год отдельно else if(Year()<Year_ || (Year()<=Year_ && DayOfYear()<DayOfYear_)) return; //тестировать весь период } // Ваш код } //+------------------------------------------------------------------+
Escolha um período de tempo:
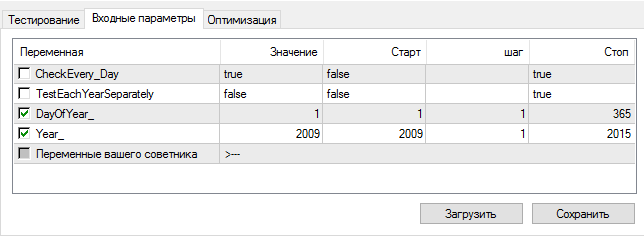
Ligue o Optimizer:
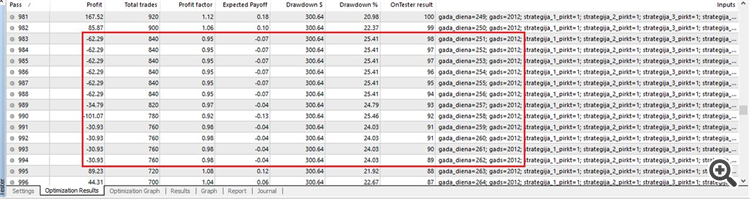
Obtemos o resultado, onde você pode ver como o Expert Advisor passa no teste a cada vez, a partir de um novo dia:
Por que a teoria da probabilidade e as estatísticas matemáticas de repente não são amadas aqui? Eles parecem estar bem aqui. Mas existem problemas com tolices baseadas na teoria da probabilidade e nas estatísticas matemáticas.
E que paradoxos?
Esta é a primeira vez que você ouve falar de paradoxos da TV e da MC?
Aqui, dê uma olhada. Há muitos bons exemplos:
SEKAI G / PARADOXOS NA TEORIA DA PROBABILIDADE E ESTATÍSTICA MATEMÁTICA
Categoria:Matemática 11 de março de 2010Título: Paradoxos na Teoria da Probabilidade e Estatística Matemática
Autor: Seksey G.
Resumo: Um livro de um matemático húngaro contendo uma coleção de conclusões e afirmações inesperadas da teoria das probabilidades, estatística matemática e teoria dos processos aleatórios É escrito de forma viva e fascinante, o material apresentado nele pode ser usado para ilustrar em palestras universitárias sobre teoria das probabilidades e algumas seções do trabalho dos círculos de matemática escolar
Para matemáticos de várias qualificações, para todos os estudantes de teoria da probabilidade e estatística matemática
Download em pdf (11,4 MB ):Sekey G. / Paradoxos na teoria da probabilidade e estatística matemática
vixri.com.
Esta é a primeira vez que você ouve falar de paradoxos da TV e da EM?
Confira. Há muitos bons exemplos:
SECEI G / PARADOXOS NA TEORIA DA PROBABILIDADE E ESTATÍSTICA MATEMÁTICA
Categoria:Matemática 11 de março de 2010Título: Paradoxos na Teoria da Probabilidade e Estatística Matemática.
Autor: Seksey G.
Resumo: O livro do matemático húngaro contendo uma coleção de descobertas inesperadas e afirmações da teoria da probabilidade, estatística matemática e teoria dos processos aleatórios. É escrito de maneira viva e fascinante, e o material nele apresentado pode ser usado para ilustração em palestras universitárias sobre teoria da probabilidade, enquanto algumas seções podem ser usadas no trabalho dos círculos matemáticos escolares.
Para matemáticos de várias qualificações, para todos os estudantes de teoria da probabilidade e estatística matemática
Download em pdf (11,4 MB ):Sekey G. / Paradoxos na teoria da probabilidade e estatística matemática
vixri.com.
E então algo ele mesmo é capaz de escrever em suas próprias palavras, ou apenas nos links, e nas telas?
Estou indo para ler um livro agora. A maior parte destes paradoxos decorre da ignorância do autor, da formulação incorreta do problema. Você tem que abrir os olhos e a mente e não existem paradoxos.
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso


O paradoxo da onipotência:
O paradoxo é geralmente formulado como uma pergunta: "Pode um deus criar uma pedra que ele mesmo não pode levantar?" (acho que sim, um ciclo infinito de criação e elevação)ou
"Poderia Deus criar um triângulo com ângulos internos que não fossem 180 graus no total?"(acho que sim, geometria Riemann).
Se Colombo tivesse sido perguntado: "É possível chegar da Europa à América em 24 horas?", penso que com as possibilidades do tempo ele teria dito não, mas hoje em dia qualquer criança dirá que é possível. A pergunta que se segue é: "Essa possibilidade já existia na época de Colombo ou só apareceu nos tempos modernos?"Teoricamente a possibilidade tem existido o tempo todo, mas na prática ela só se tornou disponível hoje. É possível concluir disto que: Qualquer coisa que não contradiga a matemática é possível, quer possamos implementá-la fisicamente ou não?As possibilidades existem quer estejamos conscientes delas ou não.