나는 당신을 이해하고 더 높은 시간 프레임 계산의 역사적 가치에 대해 동의한다고 믿습니다. 추가 데이터 포인트(낮은 시간 척도의 막대)에 해당하는 제한된 수의 막대 만 있으므로 누락된 막대를 채우거나 단계 함수를 사용하여 두 개의 더 높은 시간 프레임 값을 확장하기 위해 보간, 선형 2차 등이 필요합니다. 더 낮은 시간 프레임. 그러나 지표가 시작되면 더 낮은 시간 프레임과 더 높은 시간 프레임 모두에 동일하게 적용되는 틱 데이터 포인트별로 틱을 얻습니다. 내가 궁금한 것은 중간에 있는 하단 막대의 상단 값을 계산하고 저장하는 지표가 있는지였습니다. 예를 들어, H1 및 H4 시간 프레임을 사용합니다. H4 막대를 계산한 다음 표시기가 시작된 시간 이전에 발생한 막대에 대해 막대 N과 막대 N+1 간의 비례 차이를 사용하여 누락된 3개의 낮은 막대 값을 선형으로 보간할 수 있습니다. 내가 궁금한 것은 지표가 시작된 후 앞으로 진행되는 누락된 막대를 보간하는 대신 더 높은 시간 프레임의 중간 시간별 막대 값을 저장하고 저장하는 것입니다. 이 접근 방식을 사용하면 세 개의 간격 막대에 대한 정확한 값을 얻을 수 있습니다. 나는 지표가 시작되기 이전의 더 높은 기간 동안 역사적 중간 값 사이에 불연속성이 있다는 것을 알고 있습니다. 따라서 H4 표시기가 막대 N+1에서 1.0에서 막대 N에서 1.4로 이동하면 중간 보간 값은 1.1, 1.2, 1.3이 됩니다. 그러나 실제로 값은 N, N+1, N+2, N+3 시간의 값을 기준으로 1.0 1.3, 1.5, 1.4가 될 수 있습니다.
내가 정말로 말하는 것은 왜 MTF 표시기에 대해 상위 시간 프레임을 사용하고 대신 하위 시간 프레임 데이터 포인트를 사용하지만 모든 막대 대신 N번째 막대마다 상위 표시기를 진행하고 각각에 대한 실제 값을 사용하는 것입니다. 간격.
EMA를 사용하는 간단한 MTF 지표가 있는 경우 게시해 주시면 내 이론을 테스트하고 다시 게시하는 데 사용할 것입니다.
글쎄, 나는 테스트하고 나는 당신과 함께 괜찮습니다. 다른 사람들에 비해 정말 좋지 않습니다. Hull MA
나/우리가 말했듯이 최고의 이동 평균은 빠르고 원활해야 합니다.
그래서 내가 흥미롭다고 생각하는 다른 MA(내 그래프에서)를 테스트합니다.
적응형 T3(파란색/주황색)
NonlagMA(녹색/빨간색)
JJMA(녹색만 해당, 바이컬러 JJMA 없음)
그리고 헐
(죄송합니다, 선을 대체할 수 없기 때문에 명확하게 하기 어렵습니다)
게임의 목적은 MA를 비교하는 것이었습니다(물론 다른 기간으로)
나를 위한
적응형 T3 스무스 4/5 빠름 4/5
논랙 MA 스무스 3/5 빠름 5/5
헐 스무스 3/5 빠름 3/5
JJMA 스무스 4/5 패스트 4/5
그래서, 그냥 아이디어로, 적응형 T3(gloups...)에 의해 적응된 헐과 JJMA에 의해 적응된 헐을 만드는 것이 흥미로울 수 있다고 생각합니다. 제발 이것들을 할 수 있습니까?
나는 3개의 JMA도 비교한다(Spiggy, Starlight 및 Kositsin). 그래프에서 볼 수 있듯이 가장 좋은 것은 분명히 녹색의 Kositsin (JJMA)이고 별빛 (그리고 다시 칠할 가치가 있음)입니다. 그래프에 사용하고 이러한 Hull 적응형을 생성하는 데 사용하는 Adaptive T3 및 JJMA
보간 방법은 실제로 매우 간단합니다. 더 높은 시간 프레임의 두 끝점 사이의 선형 보간입니다(그래서 내가 보간 및 비보간(고전적인 "keris 방법") 버전이 정확히 더 높은 시간 프레임 막대당 동일한 수의 보장된 정확한 포인트: 더 높은 시간 프레임 막대마다 1개(나머지는 확률 및 가격 변동의 문제입니다.) 보간된(또는 "계단형) 값을 새로고침 상태로 둘 수 있습니다(계산 더 낮은 시간 프레임의 현재 막대만) 그러나 그러면 고전적인 다시 그리기 표시기를 얻을 수 있습니다(많은 경우 더 낮은 시간 프레임 지점의 정확한 상태를 정확하게 계산할 수 없기 때문에). 메타 트레이더가 "생존"할 것이라고 생각하지 않는다고 계산)
질문을 올바르게 이해하고 답변이 예상한 대로 되었기를 바랍니다.
안녕하세요 Mladen과 Tzuman입니다.
오랫동안 이 문제와 관련된 질문이 있습니다. 내가 더 높은 TF(EMA(H1-24 기간) 및 EMA(H4-6 기간)에 대해 동일한 MA의 길이와 동일하도록 설정된 Period_Length와 함께 Price_Close에서 더 작은 TF의 일부 유형의 MA(예: Ema 또는 LWMA)를 사용했을 때 예를 들어), 그들은 동일하지 않았습니다. 설명해 주시겠습니까?
fareastol: 안녕 Mladen과 Tzuman, 오랫동안 이 문제와 관련된 질문이 있습니다. 내가 더 높은 TF(EMA(H1-24 기간) 및 EMA(H4-6 기간)에 대해 동일한 MA의 길이와 동일하도록 설정된 Period_Length와 함께 Price_Close에서 더 작은 TF의 일부 유형의 MA(예: Ema 또는 LWMA)를 사용했을 때 예를 들어), 그들은 동일하지 않았습니다. 설명해 주시겠습니까?
파리스톨
평균에 대해 더 높은 시간 프레임 값을 얻기 위해 기간을 곱하는 것은 나쁜 방법이 아니지만(특히 Alexander Elder는 TA 초기에 이 방법을 사용했습니다) 단순히 근사치입니다. 이유는 간단합니다. 평균을 계산하는 데 사용되는 데이터 집합이 다르고 다른 데이터 집합에서 동일한 결과를 얻을 수 없습니다. 제 생각에는 다른 어떤 지표도 그런 식으로 계산할 수 없기 때문에 기존 MTF(우리가 사용하는 방식)를 사용하는 것이 좋습니다.
나는 당신의 변동성 적응 함수를 잘 연구했습니다. 왜 수학 라운드 함수를 사용하지 않습니까?
그것으로 (내가 모두 이해했다면) 적응 기간은 모든 유형의 이동 평균 또는 지표와 함께 작동 할 수 있습니다!
문안 인사.
소호쿨
한 가지 간단한 이유 때문에 : 단순히 계산 기간 을 변경할 때 일부 평균의 경우 논리적이고 가능한 한 부드러운 대신 "단계와 같은"(값의 매우 급격한 변화) 평균을 얻을 수 있습니다. 가치.
그렇기 때문에 분수 기간을 계산할 수 있는 평균만이 적응에 적합하다고 반복해서 말씀드린 것입니다. 다른 것들도 적용할 수 있지만(제한이 없음) 결과 자체는 "좋음"이 아닙니다("좋음"이 의미하는 바를 이해하시기 바랍니다). 반면에 EMA와 같은 평균은 자신의 이전 값을 "상속"하고 해당 값을 계산에 사용하며 계산은 계산 기간이 항상 변경될 때 합리적으로 매끄럽고 "논리적"으로 만드는 분수 기간을 사용할 수 있습니다.
__________________________________________
실험: SMA(특성상 기간 계산에 정수만 허용)를 적용해 보면 경우에 따라 결과가 어떻게 나타나는지 알 수 있습니다.
한 가지 간단한 이유가 있습니다. 계산 기간을 변경할 때 일부 평균의 경우 논리적이고 가능한 한 부드러운 대신 "단계와 같은"(값의 매우 급격한 변화) 평균을 얻게 됩니다. 가치.
그렇기 때문에 분수 기간을 계산할 수 있는 평균만이 적응에 적합하다고 반복해서 말씀드린 것입니다. 다른 것들도 적용할 수 있지만(제한이 없음) 결과 자체는 "좋음"이 아닙니다("좋음"이 의미하는 바를 이해하시기 바랍니다). 반면에 EMA와 같은 평균은 자신의 이전 값을 "상속"하고 해당 값을 계산에 사용하며 계산은 계산 기간이 항상 변경될 때 합리적으로 매끄럽고 "논리적"으로 만드는 분수 기간을 사용할 수 있습니다.
__________________________________________
실험: SMA(특성상 기간 계산에 정수만 허용)를 적용해 보면 경우에 따라 결과가 어떻게 나타나는지 알 수 있습니다.
안녕 믈라덴
귀하의 신속한 답변에 감사드립니다.
네, 당신의 방법이 최선임을 압니다.
그러나 interger를 사용하는 경우 단계는 (14,4)=14의 작은 단계(1 마침표 미만)가 됩니다.
그러나 interger를 사용하는 경우 단계는 (14,4)=14의 작은 단계(1 마침표 미만)가 됩니다.
그리고 시장은 그렇게 논리적이지 않습니다
소호쿨
연속 막대의 계산 기간 이 항상 비슷하지는 않을 것이라는 점을 간과하고 계시는 느낌이 듭니다. 예를 들어: 한 막대에서는 14가 되지만 다른 막대에서는 4가 됩니다. 이 경우 매우 큰 변화가 있을 것입니다. SMA를 적용하려고 하면 이와 같은 경우에 어떤 일이 발생하는지 즉시 알 수 있습니다. 따라서 분수 부분("매끄럽게" 유지하는 데 많은 도움이 됨)이 아니라 분수 마침표를 사용할 수 있다는 사실은 일반적으로 계산이 적응에 적합함을 보여줍니다(대부분의 경우 마침표가 분수일 수 있는 경우, 평균의 이전 값은 계산에서 어떤 형태로 사용되며 "상속"하지 않고는 적응할 때 정상적인 평균을 얻는 것이 거의 불가능합니다)
안녕 믈라덴
당신이 절반의 기회를 얻을 때
원래 HMA 컬러 nrp를 MTF로 만들고 보간할 수 있습니까?
이미 주위에 있고 그것을 놓친 경우가 아니면
정말 감사합니다
매우 감사WR1
다시 칠하지 않는 다중 시간 프레임 Hull 이동 평균의 한 버전이 이 게시물에 게시되어 있습니다. https://www.mql5.com/en/forum/174961/page3 (기본 매개변수(HMASpeed==2) 사용) "일반" HMA nrp)
안녕하세요 MLaden님
나는 당신을 이해하고 더 높은 시간 프레임 계산의 역사적 가치에 대해 동의한다고 믿습니다. 추가 데이터 포인트(낮은 시간 척도의 막대)에 해당하는 제한된 수의 막대 만 있으므로 누락된 막대를 채우거나 단계 함수를 사용하여 두 개의 더 높은 시간 프레임 값을 확장하기 위해 보간, 선형 2차 등이 필요합니다. 더 낮은 시간 프레임. 그러나 지표가 시작되면 더 낮은 시간 프레임과 더 높은 시간 프레임 모두에 동일하게 적용되는 틱 데이터 포인트별로 틱을 얻습니다. 내가 궁금한 것은 중간에 있는 하단 막대의 상단 값을 계산하고 저장하는 지표가 있는지였습니다. 예를 들어, H1 및 H4 시간 프레임을 사용합니다. H4 막대를 계산한 다음 표시기가 시작된 시간 이전에 발생한 막대에 대해 막대 N과 막대 N+1 간의 비례 차이를 사용하여 누락된 3개의 낮은 막대 값을 선형으로 보간할 수 있습니다. 내가 궁금한 것은 지표가 시작된 후 앞으로 진행되는 누락된 막대를 보간하는 대신 더 높은 시간 프레임의 중간 시간별 막대 값을 저장하고 저장하는 것입니다. 이 접근 방식을 사용하면 세 개의 간격 막대에 대한 정확한 값을 얻을 수 있습니다. 나는 지표가 시작되기 이전의 더 높은 기간 동안 역사적 중간 값 사이에 불연속성이 있다는 것을 알고 있습니다. 따라서 H4 표시기가 막대 N+1에서 1.0에서 막대 N에서 1.4로 이동하면 중간 보간 값은 1.1, 1.2, 1.3이 됩니다. 그러나 실제로 값은 N, N+1, N+2, N+3 시간의 값을 기준으로 1.0 1.3, 1.5, 1.4가 될 수 있습니다.
내가 정말로 말하는 것은 왜 MTF 표시기에 대해 상위 시간 프레임을 사용하고 대신 하위 시간 프레임 데이터 포인트를 사용하지만 모든 막대 대신 N번째 막대마다 상위 표시기를 진행하고 각각에 대한 실제 값을 사용하는 것입니다. 간격.
EMA를 사용하는 간단한 MTF 지표가 있는 경우 게시해 주시면 내 이론을 테스트하고 다시 게시하는 데 사용할 것입니다.
쯔만
안녕 믈라덴
글쎄, 나는 테스트하고 나는 당신과 함께 괜찮습니다. 다른 사람들에 비해 정말 좋지 않습니다. Hull MA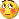
나/우리가 말했듯이 최고의 이동 평균은 빠르고 원활해야 합니다.
그래서 내가 흥미롭다고 생각하는 다른 MA(내 그래프에서)를 테스트합니다.
적응형 T3(파란색/주황색)
NonlagMA(녹색/빨간색)
JJMA(녹색만 해당, 바이컬러 JJMA 없음)
그리고 헐
(죄송합니다, 선을 대체할 수 없기 때문에 명확하게 하기 어렵습니다)
게임의 목적은 MA를 비교하는 것이었습니다(물론 다른 기간으로)
나를 위한
적응형 T3 스무스 4/5 빠름 4/5
논랙 MA 스무스 3/5 빠름 5/5
헐 스무스 3/5 빠름 3/5
JJMA 스무스 4/5 패스트 4/5
그래서, 그냥 아이디어로, 적응형 T3(gloups...)에 의해 적응된 헐과 JJMA에 의해 적응된 헐을 만드는 것이 흥미로울 수 있다고 생각합니다. 제발 이것들을 할 수 있습니까?
나는 3개의 JMA도 비교한다(Spiggy, Starlight 및 Kositsin). 그래프에서 볼 수 있듯이 가장 좋은 것은 분명히 녹색의 Kositsin (JJMA)이고 별빛 (그리고 다시 칠할 가치가 있음)입니다.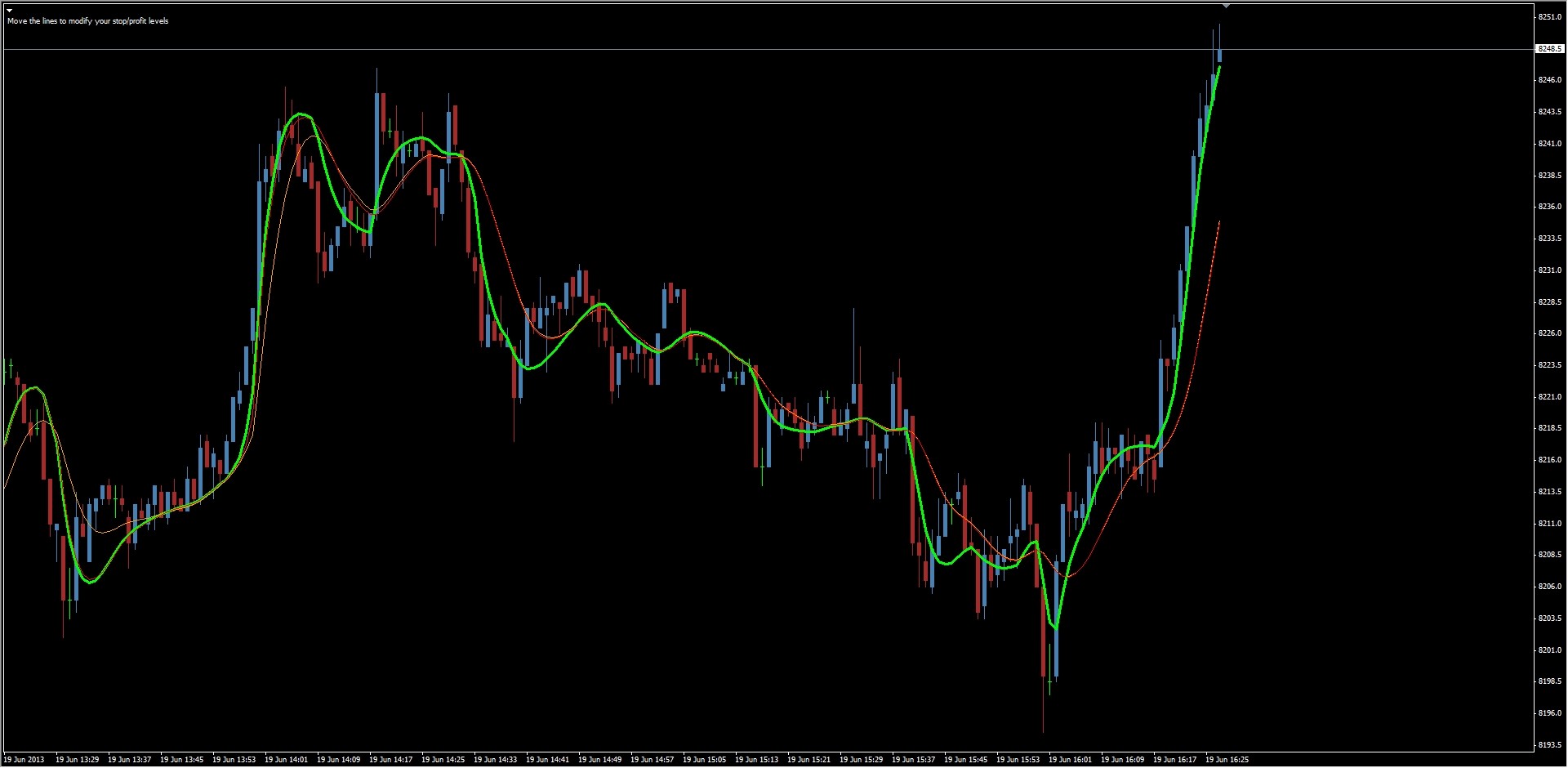
그래프에 사용하고 이러한 Hull 적응형을 생성하는 데 사용하는 Adaptive T3 및 JJMA
jjma.mq4
Adaptive_t3_mladen.mq4
Mladen 커뮤니티에 대한 수천 명의 감사
좋은 주말 되세요
질리크
Mladen님 감사합니다 집에 돌아와서 해봐야겠네요
Hull MA 및 NonlagMA와 비교하겠습니다.
당신과 함께 완전히 OK: 나는 약간의 부드러움이 있을 때 선호합니다. 빠르고 부드러움이 너무 사랑스럽습니다...
헐 변형 T3가 존재하는지 아십니까?
그리고 아마도 어리석은 일이지만 지연되지 않은 Ma로 조정된 Hull 이동 평균을 생성하고 만족하지 않습니다. Hull MA로 조정된 NonlagMa를 사용하면 결과(매끄러움)가 더 좋아질 것이라고 생각하십니까?
안녕히 주무세요
질리크
WR1 비 재도장 다중 시간 프레임 헐 이동 평균의 한 버전이 이 게시물에 게시되어 있습니다. https://www.mql5.com/en/forum/174961/page3 (기본 매개변수(HMASpeed==2) 사용) 동일 "일반" HMA nrp)
정말 감사합니다
쯔만
제가 제대로 이해하고 있는지 잘 모르겠습니다.
보간 방법은 실제로 매우 간단합니다. 더 높은 시간 프레임의 두 끝점 사이의 선형 보간입니다(그래서 내가 보간 및 비보간(고전적인 "keris 방법") 버전이 정확히 더 높은 시간 프레임 막대당 동일한 수의 보장된 정확한 포인트: 더 높은 시간 프레임 막대마다 1개(나머지는 확률 및 가격 변동의 문제입니다.) 보간된(또는 "계단형) 값을 새로고침 상태로 둘 수 있습니다(계산 더 낮은 시간 프레임의 현재 막대만) 그러나 그러면 고전적인 다시 그리기 표시기를 얻을 수 있습니다(많은 경우 더 낮은 시간 프레임 지점의 정확한 상태를 정확하게 계산할 수 없기 때문에). 메타 트레이더가 "생존"할 것이라고 생각하지 않는다고 계산)
질문을 올바르게 이해하고 답변이 예상한 대로 되었기를 바랍니다.안녕하세요 Mladen과 Tzuman입니다.
오랫동안 이 문제와 관련된 질문이 있습니다. 내가 더 높은 TF(EMA(H1-24 기간) 및 EMA(H4-6 기간)에 대해 동일한 MA의 길이와 동일하도록 설정된 Period_Length와 함께 Price_Close에서 더 작은 TF의 일부 유형의 MA(예: Ema 또는 LWMA)를 사용했을 때 예를 들어), 그들은 동일하지 않았습니다. 설명해 주시겠습니까?
안녕 Mladen과 Tzuman, 오랫동안 이 문제와 관련된 질문이 있습니다. 내가 더 높은 TF(EMA(H1-24 기간) 및 EMA(H4-6 기간)에 대해 동일한 MA의 길이와 동일하도록 설정된 Period_Length와 함께 Price_Close에서 더 작은 TF의 일부 유형의 MA(예: Ema 또는 LWMA)를 사용했을 때 예를 들어), 그들은 동일하지 않았습니다. 설명해 주시겠습니까?
파리스톨
평균에 대해 더 높은 시간 프레임 값을 얻기 위해 기간을 곱하는 것은 나쁜 방법이 아니지만(특히 Alexander Elder는 TA 초기에 이 방법을 사용했습니다) 단순히 근사치입니다. 이유는 간단합니다. 평균을 계산하는 데 사용되는 데이터 집합이 다르고 다른 데이터 집합에서 동일한 결과를 얻을 수 없습니다. 제 생각에는 다른 어떤 지표도 그런 식으로 계산할 수 없기 때문에 기존 MTF(우리가 사용하는 방식)를 사용하는 것이 좋습니다.
적응 기능 정보 .
안녕 믈라덴
나는 당신의 변동성 적응 함수를 잘 연구했습니다. 왜 수학 라운드 함수를 사용하지 않습니까?
그것으로 (내가 모두 이해했다면) 적응 기간은 모든 유형의 이동 평균 또는 지표와 함께 작동 할 수 있습니다!
문안 인사.
적응 기능 정보.
안녕 믈라덴
나는 당신의 변동성 적응 함수를 잘 연구했습니다. 왜 수학 라운드 함수를 사용하지 않습니까?
그것으로 (내가 모두 이해했다면) 적응 기간은 모든 유형의 이동 평균 또는 지표와 함께 작동 할 수 있습니다!
문안 인사.소호쿨
한 가지 간단한 이유 때문에 : 단순히 계산 기간 을 변경할 때 일부 평균의 경우 논리적이고 가능한 한 부드러운 대신 "단계와 같은"(값의 매우 급격한 변화) 평균을 얻을 수 있습니다. 가치.
그렇기 때문에 분수 기간을 계산할 수 있는 평균만이 적응에 적합하다고 반복해서 말씀드린 것입니다. 다른 것들도 적용할 수 있지만(제한이 없음) 결과 자체는 "좋음"이 아닙니다("좋음"이 의미하는 바를 이해하시기 바랍니다). 반면에 EMA와 같은 평균은 자신의 이전 값을 "상속"하고 해당 값을 계산에 사용하며 계산은 계산 기간이 항상 변경될 때 합리적으로 매끄럽고 "논리적"으로 만드는 분수 기간을 사용할 수 있습니다.
__________________________________________
실험: SMA(특성상 기간 계산에 정수만 허용)를 적용해 보면 경우에 따라 결과가 어떻게 나타나는지 알 수 있습니다.
소호쿨
한 가지 간단한 이유가 있습니다. 계산 기간을 변경할 때 일부 평균의 경우 논리적이고 가능한 한 부드러운 대신 "단계와 같은"(값의 매우 급격한 변화) 평균을 얻게 됩니다. 가치.
그렇기 때문에 분수 기간을 계산할 수 있는 평균만이 적응에 적합하다고 반복해서 말씀드린 것입니다. 다른 것들도 적용할 수 있지만(제한이 없음) 결과 자체는 "좋음"이 아닙니다("좋음"이 의미하는 바를 이해하시기 바랍니다). 반면에 EMA와 같은 평균은 자신의 이전 값을 "상속"하고 해당 값을 계산에 사용하며 계산은 계산 기간이 항상 변경될 때 합리적으로 매끄럽고 "논리적"으로 만드는 분수 기간을 사용할 수 있습니다.
__________________________________________
실험: SMA(특성상 기간 계산에 정수만 허용)를 적용해 보면 경우에 따라 결과가 어떻게 나타나는지 알 수 있습니다.안녕 믈라덴
귀하의 신속한 답변에 감사드립니다.
네, 당신의 방법이 최선임을 압니다.
그러나 interger를 사용하는 경우 단계는 (14,4)=14의 작은 단계(1 마침표 미만)가 됩니다.
그리고 시장은 그렇게 논리적이지 않습니다
안녕 믈라덴
귀하의 신속한 답변에 감사드립니다.
네, 당신의 방법이 최선임을 압니다.
그러나 interger를 사용하는 경우 단계는 (14,4)=14의 작은 단계(1 마침표 미만)가 됩니다.
그리고 시장은 그렇게 논리적이지 않습니다소호쿨
연속 막대의 계산 기간 이 항상 비슷하지는 않을 것이라는 점을 간과하고 계시는 느낌이 듭니다. 예를 들어: 한 막대에서는 14가 되지만 다른 막대에서는 4가 됩니다. 이 경우 매우 큰 변화가 있을 것입니다. SMA를 적용하려고 하면 이와 같은 경우에 어떤 일이 발생하는지 즉시 알 수 있습니다. 따라서 분수 부분("매끄럽게" 유지하는 데 많은 도움이 됨)이 아니라 분수 마침표를 사용할 수 있다는 사실은 일반적으로 계산이 적응에 적합함을 보여줍니다(대부분의 경우 마침표가 분수일 수 있는 경우, 평균의 이전 값은 계산에서 어떤 형태로 사용되며 "상속"하지 않고는 적응할 때 정상적인 평균을 얻는 것이 거의 불가능합니다)