파동 구조, 어떤 방법으로
당신은 계산이나 누구의 이론이 있습니까 ???
그리고 당신이 자세히 설명할 수 있다면.
Интересно.
간략하지만 간결하게. :에 대한)
나는 내 게시물을 다시 읽고 좋은 방법으로 다시 작성하거나 삭제해야한다는 것을 깨달았습니다. 고통스럽게 서두르다가 결국 구겨지고 어색한 것으로 판명되었습니다. 어쨌든. 이러한 보편적인 하위 시스템은 정말 흥미로운 주제입니다(적어도 관심 있는 두 사람이 이미 있습니다.) 하지만 명시적인 예측이 있는 전문가에게만 해당됩니다. 에스엘.
아마도 포럼에서 모든 것을 살펴보지는 않았지만 기본적으로 견적 프로세스를 예측하기 위해 Markov Chain(CM)을 사용하는 것이 제안되었습니다. 수학자는 아니지만 내 겸손한 이해로는 그러한 응용 프로그램이 완전히 의미가 없습니다. CM은 일반적으로 이런 종류의 프로세스와는 거리가 멀다. 그리고 더 자주 대화는 프로세스 자체의 모델이 아니라 전환 매트릭스 주위에서 짓밟힙니다. 상태와 이들 사이의 전환은 중요한 요소이지만 가장 중요한 것은 아닙니다.
분명히 CM은 주문에 따라 이동 경로를 최적화하는 문제를 해결하는 데 도움이 될 것입니다(확률적 특성을 고려한 선택). 그리고 이 "매크로 프로세스"의 속성은 CM의 속성과 고통스럽게 유사합니다. 또한 모든 종류의 미묘함이 있습니다. 예를 들어 예측은 미래에 강한 움직임을 보여주었습니다(지금은 아님). 그리고 여기에서는 지금 다른 수단에 대한 많은 거래 를 포기하고 이 예상되는 움직임에 자원(예금)을 집중하는 것이 합리적일 수 있습니다. 강한 움직임을 확인하십시오 - 전체 프로그램으로 롤업하십시오. 그렇지 않은 경우 SL이 작동하며, 이는 대안에서 트리거된 SL 주문 중 일부보다 더 수용 가능할 수 있습니다.
그러나 디지털 시장의 도움으로 최적화를 완전히 확장하고 DC의 거래 환경을 포함(또는 최소한 단순히 고려)하는 것은 불가능합니다. 여기서 선형 계획법의 요소가 필요할 것입니다.
"글쎄, 나는 너무 ka-a-a-tsa ..."(C)
세이터에게
파동 구조, 어떤 방법으로
당신은 계산이나 누구의 이론이 있습니까 ???
그리고 당신이 자세히 설명할 수 있다면.
저는 비공개 포럼에서 시스템의 개념과 일부 구성 요소에 대해 논의했습니다. 지금 당장은 공개적으로 말할 준비가 되지 않았습니다. 이론은 전적으로 내 것입니다.
흥미로운. 저녁에는 집에서 주의 깊게 읽을 필요가 있습니다.
그리고 비슷한 것을 개발 한 사람들을 토론에 초대하십시오 ...
첫 번째 게시물에 설명된 "실행 시작"으로 문제를 해결하는 데 성공하지 못했습니다. 모든 것이 그렇게 사소하지 않은 것으로 나타났습니다. 일반적으로 생각합니다.
그러나 Markov chains에 대한 선택적인 연구와 더 나은 이해로 파동 구조를 예측하기 위한 하위 시스템을 개발하려고 시도할 수 있습니다. 그들의 도움으로 가격을 직접 예측하는 것은 의미가 없지만, 다르게 접근할 수 있습니다. 내가 그렇게 말할 수 있다면 더 높은 차수의 상태를 골라내는 것입니다.
나는 이것이 완전히 새로운 아이디어라고 생각하지 않습니다. 지그재그를 대안으로 사용하는 것입니다. 다음으로 ZigZag 세그먼트에 대한 매개변수 통계를 수집합니다. 가장 먼저 생각나는 것은 세그먼트의 길이, X 및 Y 축(각각 시간 및 범위)에 대한 투영, 아마도 세그먼트 체인에 의해 형성된 영역입니다. 통계를 기반으로 분류 규칙을 개발합니다. 분류 기준으로 통계적 빈도를 취하여 다시 지그재그로 이동하면서 각 세그먼트의 분류를 동시에 수행할 수 있습니다.
실제로 ZigZag 세그먼트의 각 고유 클래스는 상태가 됩니다. 첫 번째 추정치에 따르면 이러한 상태는 3~9개 있어야 합니다. 통계 빈도에서 시작하면 얻은 빈도 값이 유의하고 서로 크게 다른 방식으로 각 매개 변수의 간격을 선택해야합니다. 다음으로, 상태 그래프를 생성하고 상태 간의 전이 행렬을 계산하는 것이 쉬울 것입니다. 여기까지는 직관적이지만 CM을 사용하여 현재 세그먼트와 다음 세그먼트만 예측할 수 있는 것 같습니다.
이 모든 것을 받으면 이미 수용 가능한 전략에 관한 몇 가지 결론을 도출하거나 거래하지 않는 것이 더 나을 때 상황에 대한 통계적 아이디어를 얻을 수 있습니다. 그것이 잘 작동한다면, 미래 클래스의 수학적 기대에 대한 경험적 공식과 같은 더 발전된 예측 모델을 얻는 것이 가능할 것입니다.
각 세그먼트 상태는 완료를 일부 영역으로 제한합니다. 사용된 분류를 통해 X 및 Y 축에서 예측된 세그먼트의 투영 평가를 진행할 수 있다는 것이 중요합니다. 웨이브 완성의 윤곽선 영역 내에서 예상되는 국부 반전 지점을 찾는 것만 남아 있습니다. 그리고 이것은 위에서 설명한 방식으로 계산하거나 Murray 수준을 사용하여 계산할 수 있습니다.
이 예측 방법은 샤머니즘 없이도 좋은 결과를 얻을 수 있고 통계적으로 정당화될 수 있습니다. 시도하기 전까지는 알 수 없는 것과 같습니다.
인터넷 어딘가에
비공개 로
Найдете вот это, все остальное что Вы написали, очень легко приложиться
개인 안녕! 나는 나의 오랜 상대를 잊었다 :o) 오, 나는 외교를 다룰 수 있다:
내가 약간 다른 목적, 즉 자산 관리, 즉 스스로 예측하기 보다는 최적의 거래 솔루션을 찾고 선택합니다. 그가 제안한 것은 말하자면 선택적인 발전의 일환으로 이론을 연구하는 것이었습니다. 그리고 위에서 쓰고 시연한 것처럼 완전히 다른 방식으로 피벗 포인트를 정의합니다.
그리고 "다른 모든 것이 따를 것"에 관해서는 - 당신은 매우 잘못 알고 있습니다. 고대 중국인의 지혜와 나의 관찰을 참조하는 것으로 충분합니다. o): 어두운 방에서, 특히 검은 고양이가 없는 순간에는 절대 검은 고양이를 찾지 못할 것입니다. 이 동료 평가를 위해 저를 전적으로 믿으십시오. 저는 검은 집 고양이가 있고 저를 믿으십시오. 제가 무슨 말을 하는지 압니다. :에 대한)))
엔젤 에
예, 저는 이 제품을 알고 있고 그것이 작동하는 논리를 상상할 수 있습니다. 컴퓨터에서 ...에서 지우고 좌파 및 우파 이론을 전혀 사용하지 마십시오. 당신의 것만 사용하십시오.
사진 감사합니다, 정말 예쁘네요. 예술가로서 나는 그것을 정말로 즐겼다. :에 대한))
제 생각에는 여기에서 일반적인 접근 방식을 찾지 않아야 합니다. 최적화 이론, Markov 체인은
몇 년 동안 뒹굴 수 있는 그 심연 - 그리고 자산 선택을 위한 특정 조건에서 춤출 수 있습니다.
그에 따라 우선 순위를 지정합니다.
비슷한 업무가 있는데 아직 구체적으로 파악하지 못했지만 조금
해결 방법에 대해 생각했습니다.
일련의 금융 상품(자산)이 있고 그에 따라 각 상품에 대한 신호가 있다고 가정합니다. 신호는 일정 시간 동안 유효합니다. 예를 들어, 일일 막대가 열릴 때 생성된 다음 다음 막대가 시작될 때까지 유효합니다. 각 악기의 신호 특성에 따라 바 내부에서 진입점을 검색합니다. 동시에 나타나는 경우
다른 기기에 대해 여러 신호를 열려면 어느 것이 우선되어야 합니까? 그 자신
첫 번째? 아니면 유리한 결과가 나올 확률이 더 높은 사람을 기다리시겠습니까?
각 도구에 대한 통계를 별도로 수집한 다음 그에 따라 수집해야 한다고 생각합니다.
이 통계로 최적의 값을 찾으십시오.
제가 이야기하고자 하는 문제는 이 포럼에서 여러 차례 반복적으로 논의되어 다양한 형태로 제시되었으며, 이에 대한 다양한 접근 방식이 제안되었습니다. 나는 다시 그것에 대해 돌아가지만 이미 특정 세부 사항을 추가하고 있습니다.
용어 규칙
상황을 설명하고 질문하기 전에 몇 가지 용어의 사용에 대해 몇 가지 유보하겠습니다. 위험 관리, 자본 관리, 투자 관리, 선택 이론 및 기타 여러 이론을 성공적으로 결합하지만 기업 및 은행 고유의 특성을 지닌 "자산 관리"라는 전체 과학이 있습니다. 이론은 "자산"의 개념 자체에 대한 광범위한 해석을 가정하지만, 이것은 그렇게 중요하지 않습니다. 트리를 따라 내 생각을 펼치지 않고 나는 그 용어를 좋아했으며 이 이론의 가장 일반적인 접근 방식은 무역과 어느 정도 공통점이 있다고 말할 것입니다. 하지만 그게 요점이 아닙니다.
본문에서 추가로 사용되는 "파동" 및 "파동 구조"라는 용어는 "지그재그"라는 용어와 유사하며 더 정확하게는 그 차이점이 논의 중인 문제에 영향을 미치지 않습니다.
문제의 공식화
언뜻 보기에 작업 설명은 매우 간단합니다. 특정 DC의 사용 가능한 예금 및 거래 규칙과 같은 기존 제한 및 위험 평가를 고려하여 별도의 하위 시스템에서 거래 작업의 최적 계획, 실행 및 제어 기능을 그룹화하는 것입니다. 이러한 아이디어는 입력 데이터의 가능한 표준화와 행동의 통계적 속성에서 다양한 거래 전략을 잘 분리한다는 가정을 기반으로 합니다.
전문가의 구성 요소로 아래에서 설명하는 하위 시스템(또는 모듈)은 "자산 관리"입니다. 전체 시스템의 기능을 보다 명확하게 표현하기 위해 그는 그림 단어의 예술적 힘에 의존했습니다. 아래 그림은 프로세스와 주요 정보 흐름의 상호 작용을 보여줍니다. 프로세스는 이후에 어떤 종류의 모듈로 패키징될 것이 분명하므로 텍스트에서 더 나아가 일반적으로 "프로세스"와 "모듈"의 다른 개념의 사용을 면밀히 모니터링하지 않을 것입니다. 그것이 지금 얼마나 중요한지는 중요하지 않습니다. 의도적으로 그림은 임의 표기법을 참조할 가능성이 높지만 IDEF를 준수하려고 했습니다. 나는 아직 데이터 형식에 대한 기술 구현 및 요구 사항을 고려하지 않고 있으며, 먼저 내가 원하는 것을 이해합니다. 그리고 나는 적어도 이것을 원합니다(개념적으로, 작업 문서는 여전히 조금 더 복잡합니다):
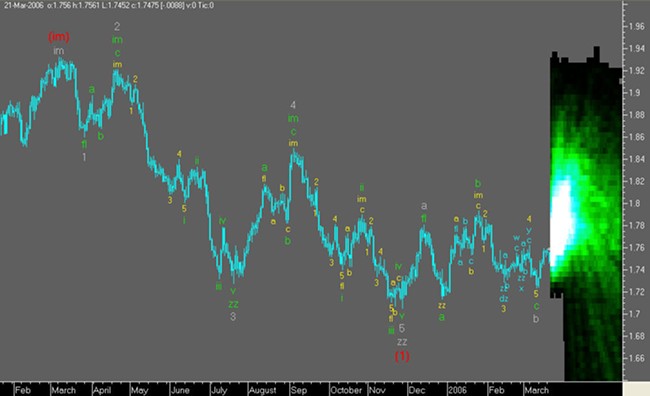
이 주제의 초점은 아니지만 예측 시스템에 대해 몇 마디 말해야 합니다. Wave Structure Forecast 하위 시스템의 개발은 세 가지 주요 단계로 나뉘며 첫 번째 단계가 최근에 완료되었으므로 이미 모든 것이 "작동하지 않아야"하는 방법을 볼 수 있습니다.o). 예측은 EURUSD, 시간, (H+L)/2와 같은 "실험실 쥐"의 예에서 보여집니다. 사실은 검은색으로 표시되고, 미래 판독값은 옅은 회색으로, 결합된 지그재그는 짙은 회색으로 표시되며, 계산된 미래 파동의 "첨부된" 세그먼트로 사실 이후에 구축됩니다.
그러한 예측으로 거래하기에는 너무 이르지만 아직 계획되지 않았습니다. 하위 시스템에 대한 작업이 완료되지 않았습니다. 다음 개발 단계에서는 예측에 정확도, 더 나은 해상도 및 더 강력한 예측 수준을 추가할 것입니다. 아마도 파도의 완료 시간이 더 정확하게 결정될 것입니다. 유감스럽게도 MathCAD가 설명자 그래픽에 가장 적합한 도구가 아니며 애니메이션에는 더욱 그렇다는 사실을 인정해야 합니다. 예측에 대한 모든 정보가 표시되지는 않습니다.
다음으로 전문가 프로세스 간의 정보 흐름을 자세히 설명합니다.
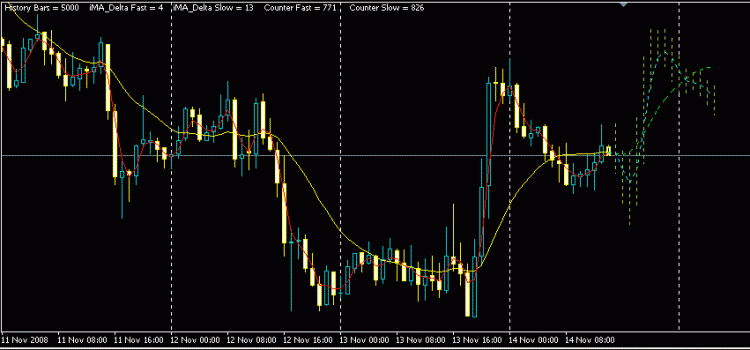
악기별 예측 . 서브시스템은 계측기의 계산된 레벨과 도달 시간을 포함하는 일련의 국부 극단값(즉, 지그재그)의 형태로 계측기의 움직임 예측을 입력 데이터로 수신한다고 가정합니다. 그들을. 기기에 대한 보편적 예측의 모양은 다음과 같이 표시됩니다.
수직 점선은 각 도구 예측에 대한 "현재" 위치를 나타냅니다. 현재 검은색으로 표시된 파도는 이미 기정사실입니다. 예측에는 "A", "B", "C" 등에서 시작하는 파도가 포함됩니다. 점선으로 강조된 웨이브 "A"는 역사에 따라 구축된 지그재그의 최종 웨이브를 정제합니다. 이에 대한 두 가지 옵션이 있을 수 있습니다. 예측에서 웨이브가 완료되고 맨 위가 과거 데이터라고 가정하거나 웨이브가 계속 발전하여 미래에 새로운 수준에 도달한다고 가정합니다.
일반적으로 이것은 중요하지 않지만 MT에서 구현할 때 좌표 간 이동할 때 고려해야 합니다. 옅은 회색으로 강조 표시된 파도는 기기 개발에 대한 예측을 계속하고 미래로 후퇴합니다.
거래 수단 . 여기에서는 모든 것이 명확합니다. 거래되는 각 상품에 대한 운영 데이터는 하위 시스템으로 전송되며, 이러한 절차가 SL 및 TP 수준을 사용하지 않고 온라인으로 수행되는 경우 이론적으로 거래를 제어 및 수정하는 데 사용할 수 있습니다.
예상 파동 수 . 논의 중인 모듈의 경우 이 매개변수는 입력의 웨이브 수를 계산하여 얻을 수 있습니다. 즉, 이 매개변수는 글로벌 수준(개발된 모듈 외부)에서 설정되며 주로 각 예측 파수(예측 깊이 수준)에 대한 예측 품질에 따라 달라집니다. 수량을 1로 설정하면 실제로 시스템이 현재 극값만 지정합니다. 현재 형성된 파동의 극단. 예측 파동의 수는 임의의 값이 될 수 있다고 가정합니다(적어도 제 의도입니다). 그러나 지금은 파도 흐름 예측을 몇 개의 파도로 제한합니다.
DC 제한 . 각 특정 DC에 고유한 거래 환경 매개변수 집합입니다. 매개변수가 나열됩니다. 이 매개변수가 자산 관리 모델에 필요할 것이라고 아직 확실하게 말할 수는 없지만 지금은 눈에 거슬리도록 두십시오.
직관적으로 유용한 것을 잊어버린 것은 아닐까? :에 대한)
각 악기에 대한 파형 구조 통계 . 위험 관리에 유용할 수 있는 중요한 통계 정보:
자산 관리 모델 . 이것이 걸림돌이있는 곳입니다. 그러한 모델이 있어야한다는 것은 분명하지만 지금까지는 정확히 그것이 무엇인지 이해하지 못합니다.
기본 기능
기능은 아직 구조화되지 않았지만 프로세스, 관계 및 논리 없이 일반 목록으로 제공됩니다.
파도의 끝 설명
제목에 공식화 된 작업은 일반적으로 최종 거래 결정이 내려지는 정보를 얻는 것과 관련이 있습니다. 예를 들어 가장 분명한 것은 SL 및 TP 수준의 계산입니다. 여기에는 근본적으로 다른 두 가지 옵션이 있습니다.
지금은 옵션 2를 고수합니다. 이러한 평가는 파도 완료 구역의 계산과 이 구역 내부의 파도 완성의 "점" 평가를 기반으로 할 수 있습니다. 영역 자체는 예를 들어 예측 및 실제 오류 통계를 사용하여 다양한 방법으로 계산할 수 있습니다. 이러한 영역의 그라데이션으로 평균 제곱 오차를 취할 수 있습니다. 다른 방법이 있습니다. 적어도 제 모델을 사용하면 대체 추정을 할 수 있습니다.
다음 문서에 설명된 원칙을 사용하여 극한 지점의 검색 및 분석을 기반으로 영역 내부의 파도 완료에 대한 지점 추정치를 얻을 수 있습니다.
- '지지 및 저항 수준을 구축하는 한 가지 방법'
- '지원 및 저항 수준 표시'
아래 그림은 X, Y로 지정된 기능 영역을 조건부로 표시한 것으로 Zone의 크기에 따라 제한됩니다. 이러한 기능은 장비의 "레벨별 밀도" 또는 파동 세그먼트의 길이 및 수명에 대한 주파수 추정일 수 있습니다. 한 경우에는 최소값을 준수해야 하고 다른 경우에는 다음 영역의 최대값을 준수해야 합니다.
따라서 예측된 파도 흐름을 설명하는 데이터 구조는 최종적으로 다음과 같은 형식을 취합니다. 파도 이동 완료 구역의 추정치가 추가되고 각 구역 내부의 기기 레벨에 대한 점 추정치가 추가됩니다.
거래 계획의 계산
일부 규정에 따라 "자산 관리" 하위 시스템은 각 도구에 대한 예측 데이터를 수신합니다. 예측 요청 신호를 보낸 후 각 도구는 자산 관리 입력에서 구성 세그먼트의 확률론적(빈도) 특성과 함께 지그재그 예측을 수신합니다. 실제로 DC의 예금 수준, 현재 거래, 수정, 위험 및 제한 사항을 고려하여 가장 최적의 "거래 체결 경로"를 찾는 것이 필요합니다. 즉, 거래 작업의 "특정" 계획(지금까지는 "안개")의 "특정" 계산을 수행합니다. 이익과 위험 사이의 적절한 균형이 어디인지에 대한 최적의 기준도 심각한 문제입니다. :에 대한)
또한 위의 내용을 통해 일반적인 경우 거래 운영 계획이 초기 웨이브 프로세스(지그재그)와 다를 수 있음이 분명해집니다. 이러한 상황은 웨이브 완료를 구체화하는 절차로 인해 발생할 수 있을 뿐만 아니라 예를 들어 아래 그림과 같이 rms 종료 오류 영역을 넘을 때도 발생할 수 있습니다.
설명된 경우 거래를 수정해야 하거나(중간 거래 거부) 이에 대한 대응으로 경로의 이 부분에서 로트가 감소할 수 있습니다. 확실히 말하기는 어렵습니다. 갑자기 연구에 따르면 그러한 작은 지그재그가 통계적으로 가장 안정적이며 더 많은 로트를 설정하는 것이 합리적이라는 것이 갑자기 밝혀졌습니다. 지금까지는 모든 것이 매우 이론적입니다.
일반적으로 거래 계획을 기반으로 "현금 흐름"을 계획하는 것이 가능합니다. 물론 이것은 어떤 형태로든 예측에 기반한(또는 기반에 가까운) 전략에만 의미가 있습니다.
거래 업무의 실행
많은 것은 거래 계획을 처리하는 특정 논리에 달려 있습니다. 직관적으로 보면 명확해 보이지만 더 자세한 설명이 필요합니다.
서비스 기능의 가용성
이것은 MT 환경에서 자동 모드로 거래할 때 발생하는 특정 기능의 일반적인 이름입니다. 가장 먼저 기억나는 것은:
동료 여러분, (회사에) 추가할 것이 있으면 쓰십시오. 그렇지 않으면 MT에서 정말 이해가 안 됩니다.
내가 무엇에 대해 묻는거야
나는 시도했고 위의 내용이 덜 명확하기를 바랍니다. 또는 다음을 사용할 수 있습니다.
전체 다양성 중에서 선택된 이론과 접근 방식을 기반으로 실제로 이익을 최대화할 수 있는 매우 효과적인 범용 자산 관리 모듈을 개발하는 것이 가능할 것 같습니다(또는 손실을 최소화하는 모든 것은 누구의 정의에 달려 있습니까? 낙관주의자). 그렇습니까? 누군가가 이미 이 경로를 밟았고 상황에 대해 밝힐 수 있습니다.
그리고 영원한 질문, 그것이 가능하다면 어떻게?
수학 분야의 전문가는 아니지만 Markov 체인 사용에 대한 몇 가지 생각이 나타났으며 가까운 시일 내에 목소리를 내기 위해 노력할 것입니다. 수학 프로그래밍에 관해서는 완전한 평신도가 있으며, 내가 아무것도 읽지 않은 동안에도 모든 것이 여전히 앞서 있습니다. 그러나 수학 프로그래밍이 무엇인지 전혀 모르는 사람들을 위한 참고 자료로 다음과 같은 일반적인 인용문이 있습니다.
Линейное программирование – целевая функция линейна, а множество, на котором ищется экстремум целевой функции, задается системой линейных равенств и неравенств. В свою очередь в линейном программировании существуют классы задач, структура которых позволяет создать специальные методы их решения, выгодно отличающиеся от методов решения задач общего характера. Так, в линейном программировании появился раздел транспортных задач.
비선형 계획법 - 목적 함수와 제약 조건은 비선형입니다. 비선형 프로그래밍은 일반적으로 다음과 같이 세분화됩니다. 볼록 프로그래밍 - 목적 함수는 볼록(최소화 작업이 고려되는 경우)이고 극한 문제가 해결되는 집합은 볼록입니다. 2차 계획법 - 목적 함수는 2차이고 제약 조건은 선형 등식과 부등식입니다.
다중 극단 문제 . 여기에서 일반적으로 볼록 함수 집합에 대한 최소화 문제와 같이 응용 프로그램에서 자주 접하게 되는 특수한 종류의 문제를 선별합니다.
선택한 접근 방식의 정확성이 실험실 연구 과정에서 확인되면 다음 논리적 단계는 구현될 "선형 프로그래밍 시스템"의 개발을 위한 기술 사양의 개발이 될 것입니다. 나는 배제하지 않으며 지정된 주제가 나뿐만 아니라 관심을 가지기를 바랍니다.
모두에게 행운을 빕니다 지그재그 통과 :o))))