Dalla teoria alla pratica - pagina 622

Nuovo commento
 
Sarebbe bello creare una squadra...come promuovere il prodotto, come crearlo, come testarlo tutto e guadagnare un po' di soldi...ma è più divertente di questo club di discussione:)
 
È davvero come una matrice che tutti guardano ma non possono vedere... tutti gli appartamenti e le tendenze hanno un inizio, hanno una fine. Siete nella matrice compagni, anche i pulsanti: rosso e blu come se Mobius lo prescrivesse) Suggerisco di tornare a Zeon per ulteriori discussioni))
 
Alexander_K2:

Kolmogorov è un uomo più intelligente della maggior parte di quelli che fissano il monitor. E i suoi requisiti per la previsione BP sono semplici: aspettativa = const e ACF periodica.

Con tali requisiti qualsiasi sciocco prevederà, figuriamoci Kolmogorov)
 
Alexander_K2:

Ora c'è una cosa da dire.

Quando guardo le distribuzioni incrementali e come cambiano i loro momenti statistici a seconda degli intervalli di lettura delle quotazioni, mi rendo conto che i prezzi di mercato NON hanno la proprietà dell'autosimilarità. Questa proprietà è unica per i processi con distribuzioni di incrementi stabili e infinitamente divisibili (per esempio normali) - come il moto browniano. Questo non è il caso del mercato.

Ovviamente, Mandelbrot e i suoi compagni, che non hanno alcuna conoscenza della fisica (e ancora peggio - hanno la conoscenza, ma la nascondono accuratamente), hanno intenzionalmente ingannato i disperati, in modo che andassero a fare scalping su dati tick e timeframes piccoli, e riempire le loro tasche inferiori perdendo i loro depositi.

Bene, ecco fatto!

Ricerca su

http://tpq.io/p/rough_volatility_with_python.html

stesso https://hal.inria.fr/hal-01350915/document
rough_volatility_with_python
rough_volatility_with_python
  • tpq.io
The code in this iPython notebook used to be in R. I am very grateful to Yves Hilpisch and Michael Schwed for translating my R-code to Python. For slideshow functionality I use RISE by Damián Avila. $$ \newcommand{\beas}{\begin{eqnarray*}} \newcommand{\eeas}{\end{eqnarray*}} \newcommand{\bea}{\begin{eqnarray}} \newcommand{\eea}{\end{eqnarray}}...
 
Alexander_K2:

Ora c'è una cosa da dire.

Guardo le distribuzioni incrementali e come cambiano i loro momenti statistici a seconda degli intervalli di lettura delle quotazioni, e mi rendo conto che i prezzi di mercato NON hanno la proprietà dell'autosimilarità. Questa proprietà è unica per i processi con distribuzioni di incrementi stabili e infinitamente divisibili (per esempio normali) - come il moto browniano. Questo non è il caso del mercato.

Ovviamente, Mandelbrot e i suoi compagni, che non hanno alcuna conoscenza della fisica (e ancora peggio - hanno la conoscenza, ma la nascondono accuratamente), hanno intenzionalmente ingannato i disperati, in modo che andassero a fare scalping su dati tick e timeframes piccoli, e riempire le loro tasche inferiori perdendo i loro depositi.

Questo è tutto!

Hai già tirato in ballo le teorie del complotto... un altro mucchio di stronzate.

Leggi l'argomento:

http://inis.jinr.ru/sl/vol2/Physics/Динамические%20системы%20и%20Хаос/Федер%20Е.,%20Фракталы,%201991.pdf

 
Ugh!
 

Solo per chiarire a cosa sto mirando.

Ho appena iniziato a lavorare nel 60° flusso di ordini di Erlang (leggendo le quotazioni in tick, in media, una volta al minuto).

Abbiamo il seguente istogramma per gli incrementi della coppia EURJPY, per esempio:

Statistiche:

Questa è praticamente una distribuzione di Laplace.

La somma degli incrementi (~prezzo) e i moduli di incremento (~dispersione) hanno una distribuzione normale a volumi di campione piuttosto grandi (un giorno - per M1 o una settimana - per M5) di tale SP.

Quindi l'obiettivo è quello di arrivare a una distribuzione di Laplace pura, allora avremo davvero un analogo diretto del processo di Ornstein-Uhlenbeck con un ritorno alla media.

 
In 600 pagine, il comandante non ha mai capito che il ritorno alla media non dipende dalla forma degli incrementi)
 

Vorrei anche indovinare quali sezioni della storia usa per costruire i suoi grafici, ci sono sezioni di tendenza per diversi mesi, e ci sono sezioni laterali

Così come il principio di "saltare" da M1 a M5 non è chiaro, ha bisogno di coerenza o almeno di una giustificazione. Sarebbe inestimabile lì con tali talenti, aggiungono anche con successo mesi, poi trimestri, poi stagioni = otteniamo i dati statistici richiesti

)))

 
Alexander_K2:

Solo per chiarire a cosa sto mirando.

Ho appena iniziato a lavorare nel 60° flusso di ordini di Erlang (leggendo le quotazioni in tick, in media, una volta al minuto).

Abbiamo il seguente istogramma per gli incrementi della coppia EURJPY, per esempio:

Statistiche:

Questa è praticamente una distribuzione di Laplace.

La somma degli incrementi (~prezzo) e i moduli di incremento (~dispersione) hanno una distribuzione normale a volumi di campione piuttosto grandi (un giorno - per M1 o una settimana - per M5) di tale SP.

Quindi l'obiettivo è quello di arrivare a una distribuzione di Laplace pura, allora avremo davvero un analogo diretto del processo di Ornstein-Uhlenbeck con un ritorno alla media.

In generale, vedo che la curtosi è ridotta, le code sono raccolte ---> da Laplace a normale, da normale a uniforme. Allora cosa c'è all'inizio, non Laplace? Perché è facilmente descritto da un esponente, se si prende un lato.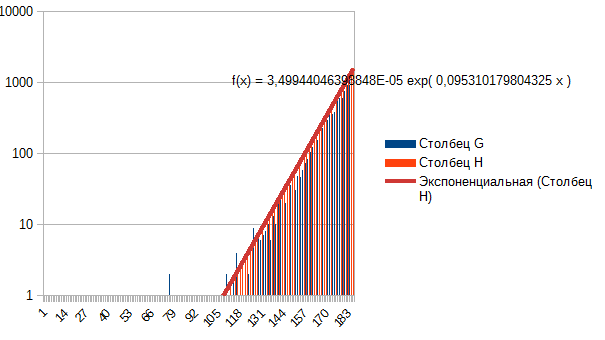 Questa è la finestra EURUSD minuto-mese.


1...615616617618619620621622623624625626627628629...1981
Nuovo commento