Ti stai perdendo delle opportunità di trading:
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Registrazione
Accedi
Accetti la politica del sito e le condizioni d’uso
Se non hai un account, registrati
Если параметры распределений Б и С различны, то формулы для вычисления МО и дисперсии будут сложнее, но все равно будет такое же распредление
Questo se C e B hanno una distribuzione stabile. In questo caso, sì, la somma delle distribuzioni stabili è uguale a una distribuzione stabile. Altrimenti, no, la somma o la differenza di C e B con distribuzioni diverse avrà una distribuzione infernale.
Если оба процесса независимые, то оба они просто шум. Если ты складываешь или вычитаешь два шума, то получаешь просто третий шум. Т.е. результирующий процесс будет
y(i) = y(i-1) + e(i), где e(i) = b(i)+s(i) или e(i) = b(i)-s(i); + или - это не имеет значения.
Случайное блуждание чистой воды. Мелкие модификации, типа типа обрезания паникёров, серьёзно ничего не изменят. Только если твои процессы будут не независимые, то могут начаться чудеса.
Grazie per la vostra risposta.
Posso introdurre un altro emendamento all'algoritmo?
Se l'eroe ha avuto il suo "incremento" - i suoi poteri e i suoi dubbi sono raddoppiati.
Come sarebbe allora questo processo prassico casuale?
Conoscendo ciò che hai modellato in modo simile - puoi guardare la campana/tubo?Questo se C e B hanno una distribuzione stabile. In questo caso, sì, la somma delle distribuzioni stabili è uguale a una distribuzione stabile. Altrimenti, no, la somma o la differenza di C e B con distribuzioni diverse avrà una distribuzione infernale.
Stiamo parlando della modellazione di passeggiate casuali, che di solito è fatta con distribuzioni stazionarie - normali o discrete. Probabilmente possiamo aggirarlo e modellarlo come non stazionario. La somma o la differenza di distribuzioni non stazionarie sarà anche non stazionaria come regola, anche se ci sono eccezioni che sono alla base della cointegrazione, per esempio
Спасибо за ответ.
можно ввести еще одну поправку к алгоритму?
Если герой получил свое "приращение" - его силы и сомнения удваиваются.
Как тогда этот случайно праксиологический процесс будет смотреться?
Зная, что вы похожее моделировали - можно колокол/трубу глянуть?Non capisco davvero. Come y(i) = y(i-1) + e(i) * i, dove e(i) = b(i)+s(i)?
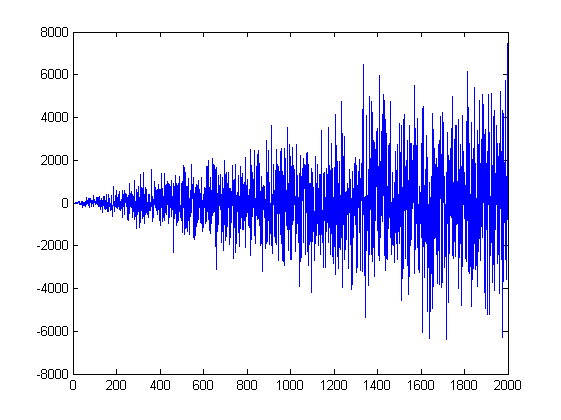
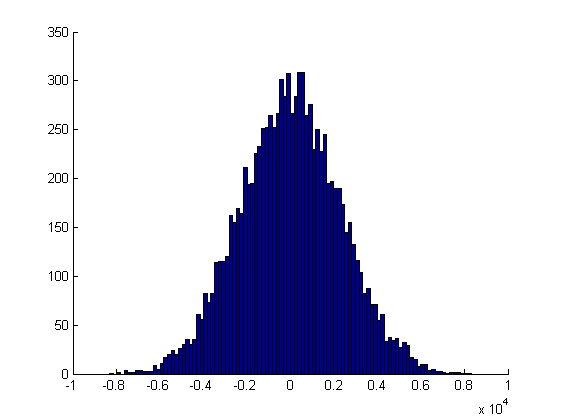
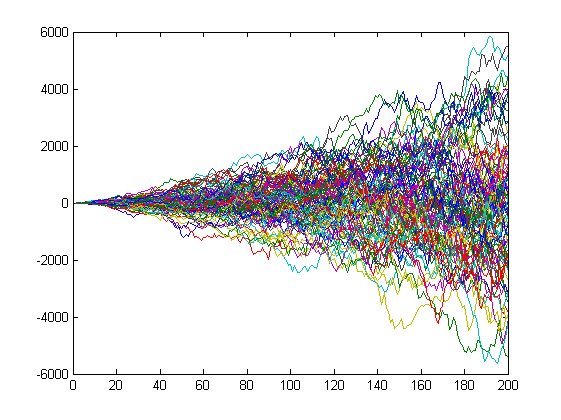
Non raddoppiando, ma aumentando. Il raddoppio crescerà troppo velocemente. Anche una semplice moltiplicazione per i dà questa crescita di incrementi
Tuttavia, il processo risultante y(i) rimane normale, che è quello che ci aspetteremmo da una passeggiata casuale.
Anche se a prima vista può non sembrare così, questo è dovuto solo al cambiamento di scala
Не очень понял. Типа y(i) = y(i-1) + e(i) * i, где e(i) = b(i)+s(i)?
Не удваивается, но возрастает. Удваивание слишком быстро вырастет. Даже простое умножение на i даёт вот такой рост приращений
Однако, результирующий процесс y(i) остаётся нормальным, чего мы и ожидаем от случайного блуждания.
Хотя оно так может и не кажется на первый взгляд, но это только из-за изменения масштаба
Sul raddoppio c'è la seguente osservazione "pratica".
Se nella fase precedente l'eroe ha ottenuto l'incremento desiderato (cioè |y(i)-y(i-1)|>= forza dell'eroe nella fase i-esima, allora la sua forza generata (compreso il meno - dubbio) nella fase i+1 dovrebbe essere raddoppiata.
Qui l'arcsina dovrebbe amplificare, ma non ne sono sicuro. Il segno-varianza si mette in mezzo ;)
---
Una richiesta sfacciata - aumentare la lunghezza dell'implementazione a 500. fuoco
На форуме часто в пылу дискуссии утверждается, что блуждание цены абсолютно случайно.
Пускай не всегда. Но случайность и не... сложно якобы отличить.
Теоремы арксинуса и двойного логарифма периодически обсуждаются или цитируются напрямую, либо только выводы.
Мутно как то...
У меня вопрос к теоретикам и практикам.
Изучал ли кто "блуждание после соударения"?
Постановка задачи следующая - есть два условных героя "БАЙ" и "СЕЛ".
Пускай генерится некое приращение для каждого из них.
В зависимости от героя назовём их "наступательным приращением" и "оборонительной силой".
...
Ci dovrebbe essere una nota a piè di pagina qui: se l'incremento è offensivo, deve per convenzione avere la precedenza sugli incrementi difensivi in mobilità,
O si deve aggiungere una costante agli RPM dopo la generazione o si deve impostare una gamma spostata di RPM.
Allora avremo un offensivo e un difensivo, altrimenti come facciamo a sapere chi è sulla difensiva?
Sul raddoppio c'è la seguente osservazione "pratica".
Se nella fase precedente l'eroe ha ottenuto l'incremento desiderato (cioè |y(i)-y(i-1)|>= forza dell'eroe nella fase i, allora la sua forza generata (compresi i meno - dubbi) nella fase i+1 dovrebbe essere raddoppiata.
Qui l'arcsina dovrebbe amplificare, ma non ne sono sicuro. Il segno-varianza si mette in mezzo ;)
Spera di determinare (o meglio, di adattare) la distribuzione del mercato con un'indovinello del genere?
супер!
О удваивании следующее "прак...ое" наблюдение.
Если на предыдущем шаге герой получил желаемое приращение (т.е |y(i)-y(i-1)|>= сила героя на i-том шаге, то его сгенерированную силу ( в том числе с минусом - сомнения) на i+1 шаге следует удвоить.
Non c'è nessun punto. Tale manipolazione cambierà la distribuzione degli incrementi, cresceranno grandi code, anche se B e C fossero normalmente distribuiti, ma non cambierà la natura del processo risultante - sarà ancora un cammino casuale e sarà normalmente distribuito. Un cammino casuale non si preoccupa della distribuzione degli incrementi finché il terzo momento è zero, cioè è simmetrico.
речь о моделировании случайных блужданий, что делается как правило стационарными распределниями - нормальным или дискретным. Можно наверное изголиться и смоделировать нестационарным. Сумма или разность нестационарных распределений будет так же нестационарна как правило, хотя есть исключения, которые лежат в основе коинтеграциии например
Non confondere caldo e morbido, cioè la stazionarietà con la distribuzione. Non sono collegati in alcun modo. Un cammino casuale ha una distribuzione normale, ma non è stazionario. Una distribuzione uniforme è stazionaria, ma la somma di due distribuzioni uniformi non sarà una distribuzione uniforme. Questa è una proprietà (mantenere il tipo/forma della distribuzione sotto qualsiasi manipolazione lineare) solo delle distribuzioni stabili.
Non confondere caldo e morbido, cioè la stazionarietà con la distribuzione. Non sono collegati in alcun modo. Un cammino casuale ha una distribuzione normale, ma non è stazionario. Una distribuzione uniforme è stazionaria, ma la somma di due distribuzioni uniformi non sarà una distribuzione uniforme. Questa è una proprietà (mantenere il tipo/forma della distribuzione sotto qualsiasi manipolazione lineare) solo delle distribuzioni stabili.
Come non è correlato? La distribuzione normale è stazionaria e gli incrementi SB distribuiti da NR sono stazionari, e io stavo parlando inizialmente degli incrementi.
Per quanto riguarda SB stesso (come somma cumulativa di incrementi): non ci saranno "code pesanti" come hai descritto nel post precedente. Perché SB stesso al tempo t è anche normalmente distribuito, ma con varianza t volte più grande che per un incremento (al tempo t dall'origine). Sì, la varianza della distribuzione SB aumenta all'aumentare del tempo. Code pesanti su 3 sigma per esempio, ma per SB se si calcola la varianza in un momento particolare (e lo si può fare analiticamente) sarà come per il normale.
Sono d'accordo che il processo SB stesso non è stazionario, è un processo inegrato con radice unitaria I(1), cioè la prima differenza (incrementi) sono distribuiti stazionari https://www.mql5.com/go?link=http://window.edu.ru/catalog/pdf2txt/141/28141/11363?p_page=55 Ma una distribuzione non stazionaria non ha necessariamente code pesanti e in questo caso non ce ne saranno
Pensate che l'HP non sia stazionario? O non si può dire per ogni distribuzione continua se è stazionaria o no? :)