Ti stai perdendo delle opportunità di trading:
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Registrazione
Accedi
Accetti la politica del sito e le condizioni d’uso
Se non hai un account, registrati
orrore, gente che butta in giro parole del genere, non è il mio posto.
Sto leggendo, cercando di capire su cosa si metteranno d'accordo.
Se è il primo tentativo di un altro agnello di mettere un paio di fronzoli su un polpo, è una cosa. Se è qualcosa di pratico, parteciperò.
Beh, Neutron è arrivato e ha messo tutto al suo posto. A proposito, marketeer parla anche della curtosi e dell'asimmetria.
La curva gaussiana corrispondente può essere tracciata come volete, ma qui è più facile calcolare semplicemente la varianza del campione e tracciare una curva gaussiana con i parametri 0 e sigma. È allora che si può vedere la differenza tra un vero istogramma e una tale curva gaussiana.
A proposito, questa approssimazione gaussiana dovrebbe essere significativamente più bassa dell'istogramma reale al centro della curva (al punto zero).
Urain, di quanto hai moltiplicato il s.c.o. dei campioni?
D'altra parte, la stima del c.s.o. per una distribuzione fortemente a coda spessa dipende dalla dimensione del campione, quindi non è così semplice in questo caso.
Non ho toccato affatto l'RMS, ho solo preso il grafico già pronto e l'ho scalato per adattarlo verticalmente all'istogramma.
L'istogramma è la distribuzione della differenza di Clos (ha ME e RMS) e questi ME e RMS sono usati per costruire la linea rossa usando la formula sopra, ma siccome la linea si perde nella parte inferiore dell'istogramma e i piccoli valori assoluti x per costruire un istogramma y proporzionale sono da biasimare, abbiamo dovuto moltiplicare ogni linea y per un moltiplicatore per il confronto.
Per la funzione di riferimento, la varianza e il MO sono presi da un certo numero di quotazioni (anch'esse calcolate lì) e impostate allo stesso valore, ma l'unica manipolazione è con i valori assoluti del benchmark, qui dobbiamo aggiungere ogni termine al coefficiente per combinare i vertici.
Per quanto ho capito, la funzione di riferimento è una funzione HP.
Se è così, hai fatto tutto bene, tranne una cosa: non puoi fare nessun dominio. Il tuo desiderio di combinare i vertici non ha nulla a che fare con la posizione effettiva dei grafici. Inoltre, il dominio viola la normalizzazione della funzione HP. Ti piace la probabilità >1?
Se togliete la dominazione e rifate la foto, le trame corrisponderanno più o meno decentemente in larghezza. Tuttavia, l'istogramma sarà più alto al centro e sui bordi, il che è indicativo di due problemi principali: maggiore rendimento e, allo stesso tempo, code pesanti.
Fai una foto come questa, se non ti dispiace.
PS
Capisco il tuo problema dal post precedente. Non c'è bisogno di violare la normalizzazione HP. È meglio trovare la scala giusta per l'istogramma. Si trova dallo stesso razionamento. Devi sommare le altezze di tutte le barre dell'istogramma e poi dividere ogni barra per questo valore. Il risultato è che anche l'istogramma è normalizzato a 1.
Sto leggendo - cercando di capire su cosa si metteranno d'accordo.
Se è un altro primo tentativo di mettere un paio di fronzoli su un polpo, è una cosa. Se è qualcosa di pratico, ci sto.
Cerchi di scoprire cosa c'è nella prima differenza di una serie di quotazioni che non è nella distribuzione normale?
Sto cercando di scoprire cosa c'è nella prima differenza delle serie di citazioni, che non è presente nella distribuzione normale?
E qual è lo scopo di questo, qual è l'obiettivo? Identificare le aree di "anormalità"? Di nuovo, perché?
(Finora solo "?????"))
E qual è lo scopo di questo, qual è l'obiettivo? Identificare le aree di "anormalità"? Di nuovo - perché?
(Finora uno "?????"))
Diciamo per sondare quale legge di anormalità si manifesta.
Ho capito che la funzione di riferimento è una funzione HP.
Se è così, hai fatto tutto bene, tranne una cosa: non puoi fare nessun dominio. Il tuo desiderio di combinare i vertici non ha nulla a che fare con la posizione reale dei grafici. Inoltre, il domaining viola la normalizzazione della funzione HP. Ti piace la probabilità >1?
Se togliete la dominazione e rifate la foto, le trame corrisponderanno più o meno decentemente in larghezza. Tuttavia, l'istogramma sarà più alto al centro e sui bordi, il che è indicativo di due problemi principali: maggiore rendimento e, allo stesso tempo, code pesanti.
Fai una foto come questa, se non ti dispiace.
PS
Capisco il tuo problema dal post precedente. Non c'è bisogno di violare la normalizzazione HP. È meglio trovare la scala giusta per l'istogramma. Si trova dallo stesso razionamento. Devi sommare le altezze di tutte le barre dell'istogramma e poi dividere ogni barra per questo valore. Il risultato è che anche il tuo istogramma è normalizzato per 1.
Beh, non è un grosso problema. Hai ancora bisogno di normalizzarlo.
Beh, non c'è nessun razionamento. Solo entrambi sono regolati su moltiplicatore=1.0/Point; altrimenti l'induttore non vede valori così piccoli.
. In basso a sinistra c'è la densità della distribuzione di probabilità, a destra - la stessa in scala logaritmica.
Se la distribuzione fosse normale, qui avremmo una parabola, cosa che non è, a causa delle code "grasse". In linea di principio, dovremmo adattare qui una gaussiana ai minimi quadrati, poi tutto andrà a posto. Dovrò inserire una formula per la misura ottimale...
Sergei, e il doppio logaritmico? È da un po' che ci penso...
Non posso ancora provarlo per modestia :)
Sergei, e il doppio logaritmico? È da un po' di tempo che ci penso...
Sono troppo modesto per controllare :)
Si scopre così:
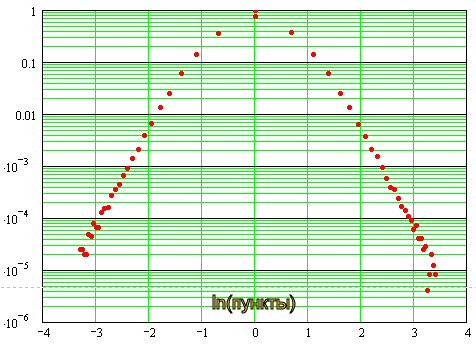
Si può vedere che vicino allo zero, la distribuzione è vicina alla normale, e poi va all'asintotica in forma di linee rette, che nella doppia scala logaritmica indica la natura esponenziale della distribuzione delle "code". In altre parole sulla loro "pesantezza".