Non vedo un ritardo nel muving. Significa che l'autore non capisce quello che ha impostato, o c'è un errore nell'algoritmo e l'indicatore si ridisegna.
Non c'è ritardo, perché non è un muwink in generale. Si risolve il problema della minimizzazione della funzione per una serie data. Naturalmente quando la serie è in movimento, se la lunghezza della serie è piccola, si ridisegnerà quando appaiono nuove informazioni, specialmente se ci sono dei picchi. Descrizione del filtro su http://en.wikipedia.org/wiki/Hodrick-Prescott_filter
In linea di principio, questa funzione è in MATLAB, se non mi sbaglio, può essere trasformata in una DLL usando il compilatore Matlab. Di conseguenza, creare un indicatore che affronti questo Dll.
Penso che il mondo sia più semplice che con un dll.
Ecco la funzione che dobbiamo minimizzare per costruire questo filtro digitale:
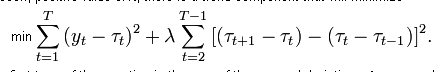
Possiamo vedere che in questa formulazione il filtro può lavorare solo su dati storici, poiché per calcolare il valore della linea di tendenza al momento attuale abbiamo bisogno di conoscere non solo i valori precedenti di questa tendenza ma anche un passo avanti t[i+1]. Un tale filtro mostrerà, sulla storia, l'esatta coincidenza della curva liscia con il kotir (questo è ciò che l'autore ha citato nel primo post come dimostrazione), mentre al bordo destro del kotir ci sarà un incredibile sovradisegno.
Ecco cos'altro ho scovato sul web:
Non ho trovato nessuna ricetta pronta per costruire questo filtro. In realtà, prendiamo e costruiamo da soli un funzionale per il bordo destro di BP (equazione superiore).
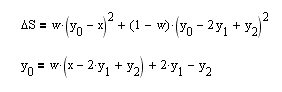
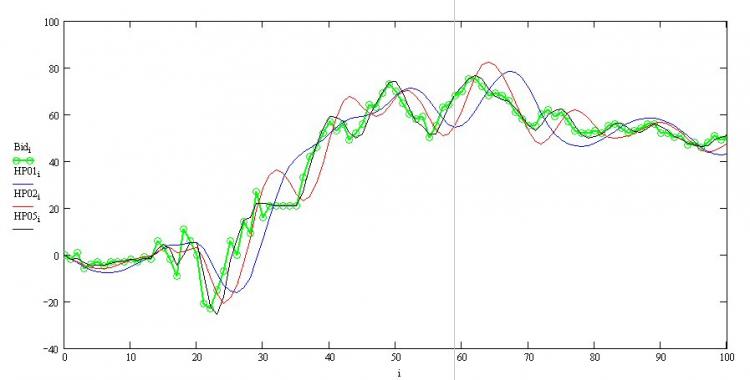
Prendiamo una derivata di essa per il parametro y[0] - valore corrente e la equipariamo a zero, e otteniamo immediatamente un'espressione ricorrente per il filtro HP richiesto (equazione inferiore). Vediamo come le proprietà di lisciatura del filtro dipendono dal parametro di lisciatura w:
Qui, la linea verde è cotier, la linea nera è w=0,5, ecc. Potete vedere che tutto funziona correttamente - c'è un inevitabile ritardo di fase che è maggiore quanto più forte è l'antialiasing e il bordo destro non viene ridisegnato. Ora possiamo codificarlo anche in MQL.
//+------------------------------------------------------------------+
//| Moving Average HP.mq4 |
//| Code by Neutron |
//+------------------------------------------------------------------+
#property indicator_chart_window
#property indicator_color1 Blue
#property indicator_width1 3
extern double w=0.1;
int Start,i,m;
double MA[5000],Y[5000];
int start()
{
Start=5000;
MA[Start]=Open[Start];
MA[Start-1]=Open[Start-1];
for (i=Start-2;i>=0;i--) MA[i]=w*(Open[i]-2.*MA[i+1]+MA[i+2])+2.*MA[i+1]-MA[i+2];
}
int init()
{
SetIndexStyle(0,DRAW_LINE);
SetIndexBuffer(0,MA);
return(0);
}
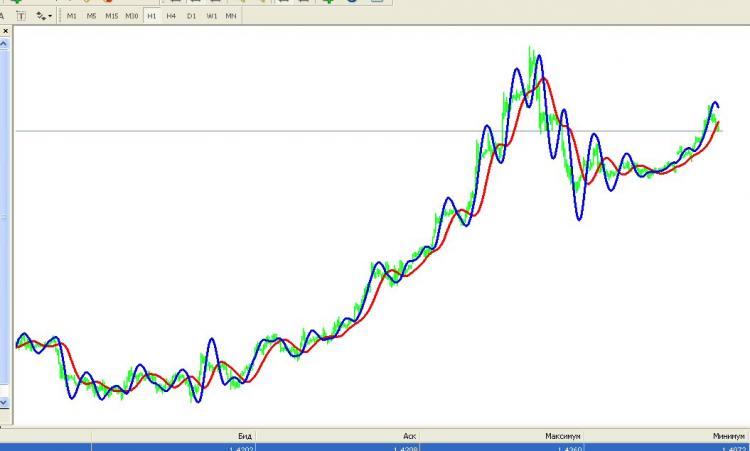
Ecco come è andata a finire:
Il blu è HP, il verde è cotier, il rosso è un filtro Watterout di 2° ordine (per confronto).
Infatti, questo filtro cerca di catturare onestamente le tendenze lineari. Guarda la funzionalità in cima al post - mostra che oltre a minimizzare la deviazione muving dal kotir (prima somma), c'è un requisito per minimizzare la derivata seconda (seconda somma)! E dopo tutto, la derivata seconda della linea è zero, e il requisito di minimizzarla è uguale al requisito di massimizzare l'aspirazione alla linea di tendenza per un vettore arbitrario di dati in ingresso. Mi è piaciuto l'approccio.
P.S. È interessante, se nell'espressione del funzionale richiediamo la minimizzazione della prima derivata (equazione superiore) invece della seconda, otteniamo una formula di ricorrenza per la media esponenziale EMA (equazione inferiore):
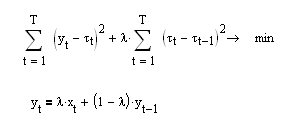
Si scopre che la media esponenziale è la più liscia di tutti i movimenti possibili!
Si scopre che la media esponenziale è la più liscia di tutti i muwings possibili
Sì, c'è un articolo sull'argomento.
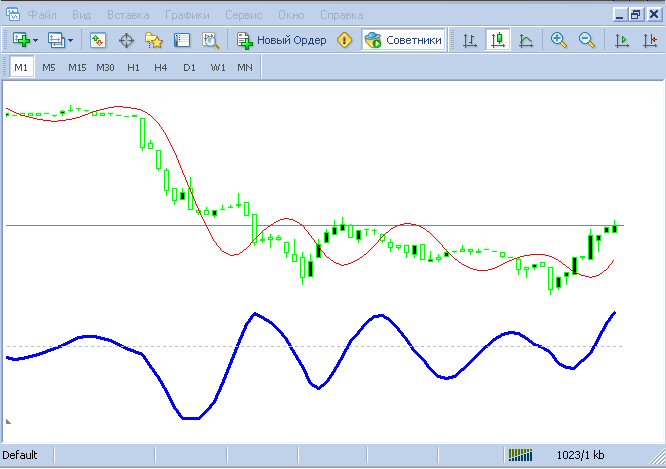
Non l'ho fatto sull'articolo, ma sviluppando la stessa idea della scorrevolezza dell'ema si può ottenere una buona scorrevolezza:
Blu - EMA15 con un ritardo di 5.
Rosso - MA più liscio con lo stesso ritardo.
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso

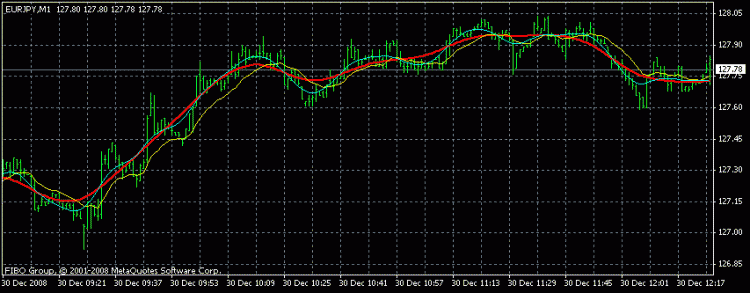
Ciao, cari programmatori!
Chi si impegnerà a risolvere, credo, un semplice compito di scrivere un indicatore? Ho bisogno di scrivere un indicatore che filtri la serie con il filtro Hodrick-Prescott. La funzione è disponibile in MATLAB, se non mi sbaglio, può essere trasformata in una DLL usando il compilatore MATLAB. Di conseguenza, abbiamo bisogno di creare un indicatore che si rivolga a questa Dll. All'ingresso dovremmo inserire i seguenti parametri - lunghezza della serie, parametro di lisciatura. L'output è una componente di tendenza (da disegnare sul grafico) e una componente ciclica (oscillatore).
Non posso farlo da solo; non conosco il compilatore MATLAB e MQL4.
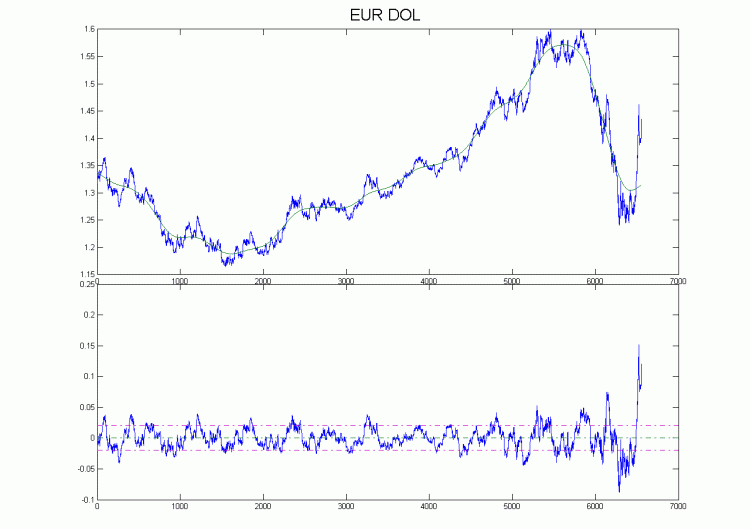
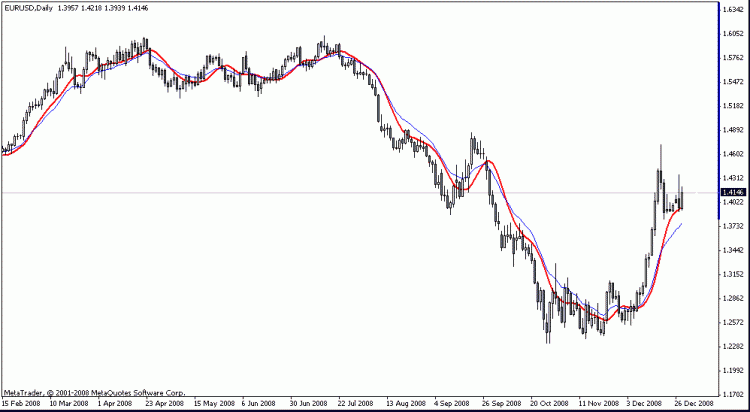
Ho una decomposizione per l'Eurodollaro H4 sul grafico. Come si è visto quasi in tutta la storia, la peculiarità del movimento dei prezzi era che dopo aver violato la tendenza, il prezzo si muoveva ad una distanza pari alla differenza tra l'estremo precedente e la tendenza, in breve, l'ampiezza era quasi la stessa. L'eccezione sono gli ultimi dati, ma lì è estrema. Fondamentalmente, un tale indicatore dovrebbe ridisegnare se il numero di punti di dati è piccolo; tuttavia, se sono aumentati, diciamo, fino a 2000, i problemi con il ridisegno non sorgeranno.