MQL5 RiferimentoLibreria StandardMatematicheStatisticheDistribuzione binomiale

Distribuzione binomiale

Questa sezione contiene funzioni per lavorare con la distribuzione binomiale. Esse permettono di calcolare la densità, probabilità, quantili e di generare numeri pseudo-casuali distribuiti secondo la legge binomiale. La distribuzione binomiale è definita dalla seguente formula:

dove:

x — valore della variabile casuale

n — numero di test

p — probabilità di successo per ogni test

DemoBinomialDistribution

Oltre al calcolo delle singole variabili casuali, la libreria implementa anche la capacità di lavorare con array di variabili casuali.

Funzione	Descrizione
MathProbabilityDensityBinomial	Calcola la funzione di densità di probabilità della distribuzione binomiale
MathCumulativeDistributionBinomial	Calcola il valore della funzione di distribuzione di probabilità binomiale
MathQuantileBinomial	Calcola il valore della funzione di distribuzione binomiale inversa per la probabilità specificata
MathRandomBinomial	Genera una variabile/array di variabili pseudocasuali distribuite secondo la legge binomiale
MathMomentsBinomial	Calcola i valori numerici teorici dei primi 4 momenti della distribuzione binomiale

Esempio:

#include <Graphics\Graphic.mqh>
#include <Math\Stat\Binomial.mqh>
#include <Math\Stat\Math.mqh>
#property script_show_inputs
//--- parametri di input
input double n_par=40;        // il numero di tests
input double p_par=0.75;      // probabilità di successo per ogni test
//+------------------------------------------------------------------+
//| Funzione start del programma Script                              |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- nascondere il grafico(chart) dei prezzi
   ChartSetInteger(0,CHART_SHOW,false);
//--- inizializza il generatore di numeri casuali
   MathSrand(GetTickCount());
//--- genera un esempio della variabile casuale
   long chart=0;
   string name="GraphicNormal";
   int n=1000000;       // il numero di valori nell'esempio
   int ncells=20;       // il numero di intervalli nell'istogramma
   double x[];          // centro degli intervalli dell'istogramma
   double y[];          // il numero di valori dall'esempio che cade all'interno dell'intervallo
   double data[];       // esempio di valori casuali
   double max,min;      // i valori massimo e minimo nell'esempio
//--- ottiene un campione dalla distribuzione binomiale
   MathRandomBinomial(n_par,p_par,n,data);
//--- calcolare i dati per tracciare l'istogramma
   CalculateHistogramArray(data,x,y,max,min,ncells);
/ --- ottiene i dati teoricamente calcolati in base all'intervallo di [min, max]
   double x2[];
   double y2[];
   MathSequence(0,n_par,1,x2);
   MathProbabilityDensityBinomial(x2,n_par,p_par,false,y2);
//--- imposta la scala
   double theor_max=y2[ArrayMaximum(y2)];
   double sample_max=y[ArrayMaximum(y)];
   double k=sample_max/theor_max;
   for(int i=0; i<ncells; i++)
      y[i]/=k;
//--- output charts
   CGraphic graphic;
   if(ObjectFind(chart,name)<0)
      graphic.Create(chart,name,0,0,0,780,380);
   else
      graphic.Attach(chart,name);
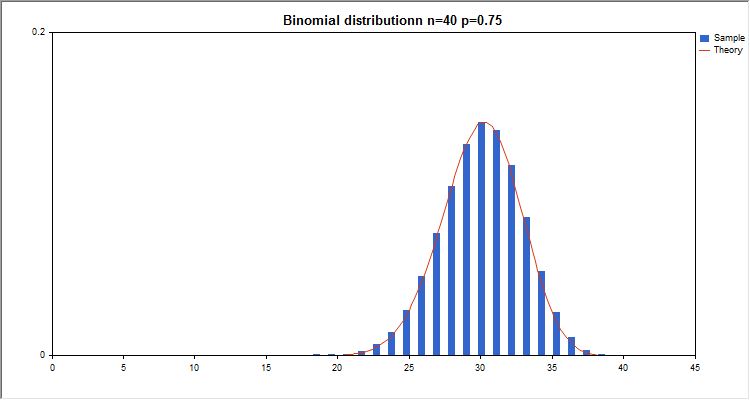
   graphic.BackgroundMain(StringFormat("Binomial distributionn n=%G p=%G",n_par,p_par));
   graphic.BackgroundMainSize(16);
//--- disegna tutte le curve
   graphic.CurveAdd(x,y,CURVE_HISTOGRAM,"Sample").HistogramWidth(6);
//--- e ora tracciare la curva teorica della densità di distribuzione
   graphic.CurveAdd(x2,y2,CURVE_LINES,"Theory").LinesSmooth(true);
   graphic.CurvePlotAll();
//--- disegna tutte le curve
   graphic.Update();
  }
//+------------------------------------------------------------------+
//| Calcolare le frequenze per set di dati                           |
//+------------------------------------------------------------------+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
                             double &maxv,double &minv,const int cells=10)
  {
   if(cells<=1) return (false);
   int size=ArraySize(data);
   if(size<cells*10) return (false);
   minv=data[ArrayMinimum(data)];
   maxv=data[ArrayMaximum(data)];
   double range=maxv-minv;
   double width=range/cells;
   if(width==0) return false;
   ArrayResize(intervals,cells);
   ArrayResize(frequency,cells);
//--- definire il centro dell'intervallo
   for(int i=0; i<cells; i++)
     {
      intervals[i]=minv+(i+0.5)*width;
      frequency[i]=0;
     }
//--- riempie le frequenze di caduta all'interno dell'intervallo
   for(int i=0; i<size; i++)
     {
      int ind=int((data[i]-minv)/width);
      if(ind>=cells) ind=cells-1;
      frequency[ind]++;
     }
   return (true);
  }

MathMomentsWeibull

MathProbabilityDensityBinomial