Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
Estoy tratando de entender el origen de tus números x y P(x), creo que tal vez el inglés no es tu primer idioma por lo que quiero asegurarme de que entendemos el significado de los términos que estás utilizando antes de hacer cualquier conclusión o declaración confusa.
"con un riesgo constante del 0,5% por operación"
¿Qué es un riesgo del 0,5% por operación? ¿Significa que está arriesgando el 0,5% del saldo de la cuenta en el caso de que el mercado se mueva en contra de su posición y la posición se cierre al precio del stoploss?
"eso significa que tengo un 0,35% de estar al 50% del saldo de mi cuenta"
El riesgo de ruina es un cálculo de factor tiempo, lo que significa que las unidades de la declaración que haces con los números que calculas se entiende que son "por operación" o "por semana" o "por mes".
En este momento no puedo decir de dónde vienen x y P(x) pero eso determina las unidades involucradas aquí.
Ayúdame a entender lo que has hecho y estaré más que feliz de invertir el tiempo en determinar si estás aplicando los cálculos correctamente.
hola philip
y gracias por ayudarme aquí :)
El 0,5% de riesgo por operación significa exactamente eso. Es la cantidad que pierdo si el mercado se mueve en contra de mi posición y alcanza el SL.
El valor de 0,35% es para el período de toda la prueba ( que es un período de unos 8 años.... ), X y P(X) ambos tomados de este informe también.
¡No puedo entender para qué período de tiempo será lógico hacer este cálculo!
tomemos el periodo del 10.01.2001 - 10.01.2002
¿Será lógico calcular el factor en ese período? ¿Hay suficientes datos para determinar la relación entre las operaciones ganadoras y las perdedoras?
Espero haber sido claro esta vez :)
La forma de utilizar los cálculos de riesgo de ruina consiste en definir un periodo de tiempo (mensual, semanal, anual, etc.) o un incremento de algún tipo (por operación, por 10 operaciones, etc.) y, a continuación, reunir las estadísticas de esos periodos. Es importante en términos de lo que la salida resultante de la calc de riesgo de ruina realmente significa (sus unidades).
A veces es útil centrarse primero en asegurarse de que se está haciendo la pregunta correcta (en otras palabras, asegurarse de que la respuesta que se está tratando de calcular va a responder realmente a la pregunta que se necesita/quiere responder).
Por ejemplo, mis clientes trabajan con un calendario mensual. No se preocupan por las cosas diarias o semanales, para ellos todo gira en torno a los resultados mensuales. Por lo tanto, en mi caso no sirve de nada que calcule el riesgo de ruina para los resultados semanales o por operación.
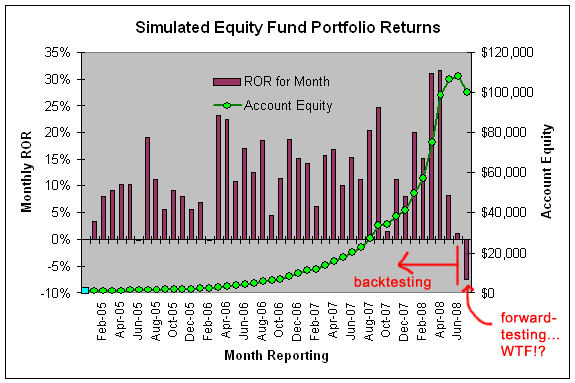
Por lo tanto, lo que debo hacer en el backtest es capturar la tasa media de retorno (ganancias, pérdidas, ROR, etc) sobre una base mensual. Algo así como lo siguiente:
Para calcular las métricas de riesgo de ruina primero debes reunir los datos para tu marco temporal. En mi caso, en este ejemplo, necesitaba reunir los resultados de la tasa de rendimiento mensual, calcular la ROR mensual media y, a continuación, calcular la desviación estándar de esas tasas de rendimiento mensuales.
En este ejemplo, la ROR media mensual fue del 12% con una desviación estándar del 8%... a partir de los resultados del backtesting esto debería haber sido oro en el futuro, sólo que no lo fue (como puedes ver). Tenga en cuenta que me refiero al riesgo de ruina como riesgo de pérdida (ROL), ya que no estoy interesado en saber cuándo se arruinará mi cuenta (esa es la cuestión trivial), sino que estoy más interesado en saber con qué frecuencia debo esperar que la cuenta se sumerja en una cantidad fija, digamos un 20%.
Así que una ROR del 12% mensual con una desviación estándar del 8% significa que puedo esperar que mi cuenta experimente una pérdida del 7,4% del valor de la cuenta alrededor del 6,5% de las veces (el 6,5% de los eventos de fin de mes, o aproximadamente una vez cada 15 meses).
Así que, aunque al principio me pilló desprevenido el aparentemente inexplicable resultado de la prueba a plazo, era perfectamente razonable esperar ese resultado mensual basándome en los resultados de las pruebas retrospectivas, una vez cada 15 meses puedo esperar una reducción tan negativa en el valor máximo de mi cuenta.
Así que ya ves, para que puedas calcular una evaluación significativa del riesgo de pérdida, primero debes decidir qué período de tiempo es pertinente para ti y luego debes reunir los resultados en una forma que sea susceptible de calcular la media y la desviación estándar del RoR en ese período de tiempo.
Una vez que disponga de los datos del backtest, podrá realizar un sinfín de análisis estadísticos utilizando cálculos de riesgo de ruina (o riesgo de pérdida, como me gusta llamarlo).
¡¡Tengo muchas preguntas!!
para empezar....
1- En sus cálculos mensuales, ¿asumen un tamaño de posición constante?
2- ¿Cada prueba mensual se hace sobre el depósito inicial ? independientemente del progreso de los meses anteriores ?
asumiendo que la respuesta a las dos primeras preguntas es SÍ :)
He calculado la ROR para 14 grupos de 100 operaciones
Utilicé un tamaño de lote de 0,01 y realicé el cálculo sobre el depósito inicial de 700 dólares para cada grupo
y obtuve los siguientes resultados :
(Tengo que instalar excell no ... ? )
1-> 0%
2-> + 12%
3-> 0%
4-> + 18%
5-> - 3%
6-> -8%
7-> +22%
8-> -3%
9-> +11%
10-> +23%
11-> +17%
12-> +7%
13-> -8%
14-> +2%
a partir de estos datos he obtenido una ROR media del 6,5% con una desviación estándar del 10,47%
Ahora no estoy seguro de cómo calcular la segunda parte:
"Así que una ROR del 12% mensual con una desviación estándar del 8% significa que puedo esperar que mi cuenta experimente una pérdida del 7,4% en el valor de la cuenta alrededor del 6,5% de las veces (6,5% de los eventos de fin de mes, o aproximadamente una vez cada 15 meses)."
¡¡Tengo muchas preguntas!!
para empezar....
1- En sus cálculos mensuales, ¿asumen un tamaño de posición constante?
2- ¿Cada prueba mensual se hace sobre el depósito inicial ? independientemente del progreso de los meses anteriores ?
Sí, el backtesting DEBE hacerse siempre sin la composición en vigor si se desea eliminar el sesgo de la cronología de los eventos en el análisis. Debemos colocar cada evento (operación) con la misma ponderación que cualquier otro evento si pretendemos emplear análisis estadísticos no ponderados (como tomar la media y la desviación estándar, etc.). Sospecho que ya es consciente de ello.
Cuando se realizan pruebas a futuro/pruebas en vivo, hay que tomar una decisión: ¿quieres que la prueba a futuro se centre en ganar dinero (entonces debería estar en vigor la capitalización) o quieres que la prueba a futuro siga generando datos que sean susceptibles de estos tipos de análisis estadísticos?
Debo señalar que en el límite matemático del período de muestreo que se hace lo suficientemente pequeño como para capturar una operación, los factores de sesgo estadístico llegan a la unidad (uno), por lo que los errores introducidos al ignorar el hecho de que el sesgo estadístico está en efecto pueden ser mínimos en esas situaciones.
El punto de todo este galimatías es decir que usted tiene que tomar decisiones, tanto en lo que respecta a sus pruebas retrospectivas, así como sus pruebas a futuro (o el comercio en vivo) y si desea que las estadísticas entre los dos para ser comparables en un sentido matemático, entonces usted necesita para asegurarse de que ha gestionado la prueba retrospectiva de tal manera que hace que los datos resultantes susceptibles de mapeo (otro término matemático) a las estadísticas pertinentes para las pruebas a futuro.
Hacer las pruebas retrospectivas con un tamaño de lote fijo e invariable con respecto al saldo inicial de la cuenta es la única manera de hacerlo en las pruebas retrospectivas.
asumiendo que la respuesta a las dos primeras preguntas es SÍ :)
He calculado la ROR para 14 grupos de 100 operaciones
Utilicé un tamaño de lote de 0,01 y realicé el cálculo sobre el depósito inicial de 700 dólares para cada grupo
y obtuve los siguientes resultados :
(Tengo que instalar excell no ... ? )
1-> 0%
2-> + 12%
3-> 0%
4-> + 18%
5-> - 3%
6-> -8%
7-> +22%
8-> -3%
9-> +11%
10-> +23%
11-> +17%
12-> +7%
13-> -8%
14-> +2%
de estos datos he obtenido una ROR media del 6,5% con una desviación estándar del 10,47%
Ahora no estoy seguro de cómo calcular la segunda parte:
"Así que una ROR del 12% mensual con una desviación estándar del 8% significa que puedo esperar que mi cuenta experimente una pérdida del 7,4% en el valor de la cuenta alrededor del 6,5% de las veces (6,5% de los eventos de fin de mes, o aproximadamente una vez cada 15 meses)."
Una vez que tenga los datos de la prueba retrospectiva, y siempre que los datos se preparen como se ha comentado en el post anterior, puede elegir qué ecuación desea utilizar para calcular su riesgo de pérdida futuro.
¿Va a utilizar la capitalización o no? Si NO tiene intención de utilizar la capitalización, la ecuación es sencilla:
Y así calculamos su R (la frecuencia para la que puede esperar que su cuenta baje un 10% después de 100 operaciones) como:
Así que en este ejemplo, la pregunta es "¿con qué frecuencia puedo esperar que mi cuenta experimente al menos una reducción del 10% de la marca de agua alta después de 100 operaciones?" la respuesta es "30,5% de las veces esto sucederá".
O para darle la vuelta, podría decir "mi cuenta debería bajar un 10% de su marca de agua alta al menos una vez cada tres períodos de 100 operaciones". Esto es así si no hace uso de la capitalización.
Si usted tiene la intención de hacer compounding en su cuenta para pruebas a futuro o pruebas en vivo, entonces usted utiliza el mismo RoR% y stand-dev (ya que los generó sin biaising de cronología de eventos, pueden ser mapeados para este uso también) entonces usted simplemente utiliza la fórula más complicada:
Y así calculamos R para un método de comercio compuesto que se construye sobre una estrategia de comercio como la que has desarrollado y obtenemos:
En este caso, la diferencia entre la capitalización y la no capitalización apenas afecta al riesgo de pérdida calculado (30,6% frente a 30,5%), como era de esperar, pero la capitalización siempre será peor que la no capitalización (al menos desde el punto de vista estadístico) si su ratio de Sharpe es inferior a 1. (el suyo es de 0,62, muy por debajo de 1).
No estoy seguro de que estamos en la misma página aquí ...
las fórmulas son bastante conocidas...
sin embargo, ¿tiene realmente sentido tener un 30,5% de posibilidades de perder al menos el 10% del saldo de la cuenta para la distribución de los valores en la mano?
¡considere el hecho de que para este conjunto de 14 valores el máximo drawdown fue del 8% que se repitió sólo dos veces y nunca por debajo !
así que el 30,5% para tener un drawdown del 10%+ parece bastante desproporcionado aquí...
Hice mi propia investigación y traté de calcular la probabilidad de tener un drawdown de 10%+ y obtuve un resultado diferente
Utilicé la siguiente fórmula:
X es una variable aleatoria de una distribución normal con media μ y desviación estándar σ
X = - 10%
µ = 6.5%
σ= 10.47%
debido a la naturaleza simétrica de la distribución normal puedo utilizar + 1,576
La probabilidad acumulada hasta Z viene dada por -> Φ(t)=P(Z≤t)
pero tengo que calcular el acumulado complementario que es 1-Φ(t) = 1 - P(1.576) = 1 - 0.9418 = 0.0582 = 5.8%¿tiene algún sentido? ¿estamos hablando de lo mismo?
X es una variable aleatoria de una distribución normal con media μ y desviación típica σ
X = - 10%
µ = 6.5%
σ = 10.47%
pero necesito calcular el acumulado complementario que es 1-Φ(t) = 1 - P(1.576) = 1 - 0.9418 = 0.0582 = 5.8%¿tiene algún sentido? ¿estamos hablando de lo mismo?
¿Es µ aquí la reducción media o es la tasa media de rendimiento? ¿Y es σ aquí la desviación estándar de la reducción o es la desviación estándar del RoR? ¿El acumulado complementario es la probabilidad de una reducción del 10% o la probabilidad de una tasa de rendimiento del -10%?
Según entiendo, está usted confundiendo sus valores de riesgo de rentabilidad con los de riesgo de caída. Si quiere calcular las estadísticas del riesgo de caída, tiene que calcular la caída de cada operación (no las ganancias/pérdidas, sino la caída transitoria mientras la operación estaba "en vivo") de manera que pueda calcular la caída media por operación y el stddev, entonces el valor acumulativo complementario representará lo que está pensando.
Estamos hablando del riesgo de ruina (concretamente del riesgo de pérdida, un caso aún más generalizado del cálculo del riesgo de ruina). Revisa este artículo, quiero decir que lo leas de verdad y no te limites a glosar el matiz específico de las palabras empleadas.
En la página dos tenemos un cálculo muy sencillo para calcular el riesgo de perder 1 sigma, su sigma es el 10,47%. El riesgo de perder el 10,47% depende de su tasa media de rendimiento, que en su caso es del 6,5%. Su sharpe está por debajo de 1 (normalmente no se considera algo bueno) y su riesgo de perder el 10,47% (1-sigma) es del 29,1%.
Fíjate en la ordenada y la abscisa de este gráfico, la gente se confunde con esto todo el tiempo. El eje de ordenadas debería inspirar unas cuantas preguntas clave en su mente, y responderlas le llevará por el camino de la comprensión de lo que significa la reducción. Pregúntese "¿cómo es que tengo una probabilidad cercana al 100% de incurrir en una pérdida del 0,1%?".
Piense en ello, piense en lo que estamos calculando con el riesgo de pérdida/ruina, piense en cómo es el gráfico de la equidad vs. el tiempo de su operación y comprenda que cada vez que establece un nuevo máximo y luego retrocede ligeramente, este retroceso tan leve es un drawdown desde el nuevo máximo establecido.
En cualquier caso, la gente no tiende a contemplar el riesgo de pérdida con respecto a 1-sigma, sino que tiende a pensar en términos de 50/50 como si se tratara de un lanzamiento de moneda. Entonces, ¿cuál es la cantidad de capital que su cuenta puede perder el 50% de las veces? Respuesta: 6%
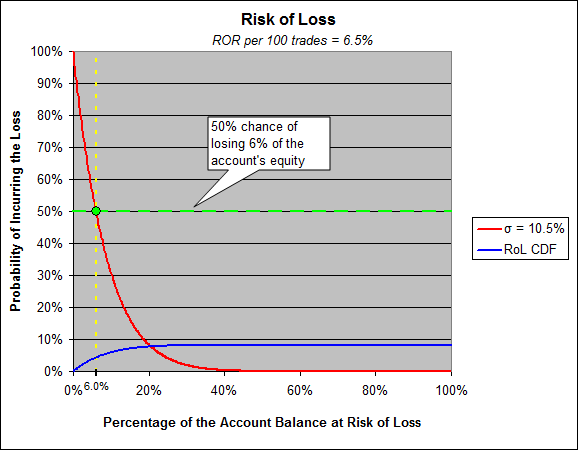
Tiene un 50/50 de posibilidades de perder el 6% al final de cualquier ronda de 100 operaciones.
También hay que entender que este cálculo se basa en las estadísticas de sólo 14 muestras, generalmente nos referimos a los números producidos por estos cálculos como "límites inferiores". Lo que significa que mientras calculamos que usted puede perder el 6% del capital de su cuenta el 50% de las veces, también tomamos ese valor para significar realmente "al menos el 6%, pero probablemente más alto debido a factores de riesgo no contabilizados".
Hay una razón por la que el 75% de la gente pierde dinero en Forex a pesar de tener backtests que muestran que su estrategia es el santo grial. Tienen los datos a su disposición (es decir, pueden generar los datos que necesiten) para calcular el riesgo de ruina, pero les venden la esperanza y los sueños que es el factor de beneficio y el pago esperado, etc.
Pero no te fíes de mi palabra, tienes el artículo, pásate por David y pregunta, le gusta hablar del tema. Y ponlo a prueba. Coge tu estrategia backtested y ponla en un test forward y mira lo que pasa. (¿has mirado mis resultados arriba cuando yo mismo hice este experimento sin saberlo?)
(y hay otra pepita de epifanía financiera por descubrir en los análisis de riesgo de pérdidas, descubrirás por qué el Ratio de Sharpe es tan venerado entre los analistas financieros y entonces te darás cuenta de su principal debilidad y de por qué la gente dice que "la beta mata")
OK
Creo que lo tengo. Gracias
volveré con más preguntas mañana :)
Oh ...
Hay una cosa que todavía no entiendo.... ¿no hay otros factores que influyen en este cálculo?
Tomemos sus resultados de ROR calculados sobre una base mensual
Supongamos (por el bien del argumento) que cuantas más operaciones haya en un mes, mayor será la ROR que obtenga
por ejemplo: para 0 operaciones usted gana 0%
con 10 operaciones gana un 5% (de media)
por 20 operaciones se gana un 10% (de media)
y así sucesivamente...
Supongamos que en ese periodo de 30 meses hubo una gran dispersión de valores en la distribución de la ROR ( para cada mes hubo un número completamente diferente de operaciones realizadas )
de modo que la rentabilidad media es del 10% y la desviación estándar es del 20% y no hubo una ROR negativa ( no se puede tener un número negativo de operaciones... )
ahora el cálculo del riesgo de pérdida de una desviación estándar que es del 20% nos dará aproximadamente el 37% ... que realmente no tiene ningún sentido ..
¿Ves a dónde quiero llegar?