El fenómeno de San Petersburgo. Las paradojas de la teoría de la probabilidad. - página 4
Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
En este hilo, por favor, publica cualquier paradoja de la teoría de la probabilidad que puedas encontrar.
Gabor Sekei. Paradojas en la teoría de la probabilidad y la estadística matemática.
http://baguzin.ru/wp/wp-content/uploads/2016/05/Габор-Секей.-Парадоксы-в-теории-вероятностей-и-математической-статистике.pdf
¿Pero qué pasa si es del 0 al 5, o al 7, o a cualquier otro número? Todavía tienes que dividir por 32768,0. ¿O hay opciones?
Por supuesto, así es como debe ser:
Novaja:
В этой теме прошу выкладывать разные парадоксы теории вероятности, все, какие можно найти.
Rompecabezas matemáticos y diversión
Este libro del famoso divulgador científico estadounidense M. Gardner tiene un montón de problemas y acertijos muy entretenidos de diferentes ramas de las matemáticas. Una acertada selección de material, una forma de presentación bastante inusual y el sutil humor del autor harán las delicias de un amplio abanico de lectores, amantes de las matemáticas que quieran pasar de forma provechosa su tiempo libre.
Fuente:
Gardner M. 'Puzzles matemáticos y diversión'. \\Traducido del inglés por Danilov Y.A., editado por Smorodinsky Y.A. - Moscú: Mir, 1971 - p.511
Así es, por supuesto, como debería ser:
Sin utilizar el resto de la división.
Sin utilizar el resto de la división.
Creo que la "no aleatoriedad" sólo se notaba realmente a la hora de definir pares, impares.
Si se utiliza un resto de división de números mucho más grandes que 2, es poco probable que sea detectable.
La única forma correcta es utilizar números que sean 2 a la potencia de N en lugar de 100, por ejemplo, 64, 128, 256...
Pero la reducción de rand() a doble de 0 a 1 también es normal, porque es más fácil de entender un valor aleatorio y más preciso, aunque un poco más lento. Pero creo que estamos hablando de fracciones de nanosegundo, aunque pueden ser nanosegundos, porque el procesador necesita cambiar de operaciones int a operaciones dobles(mezcla FPU/ALU), y Renat dijo una vez que esto no es ni mucho menos gratis.
En este hilo, por favor, publica las paradojas de la teoría de la probabilidad que puedas encontrar.
https://oschool.ru/files/studys/55df78bc740d76b70e8b4287/1443032585656.pdf
¿Ha visto personalmente a un jugador acertar y no recibir las ganancias? Nunca he visto ganar a nadie, excepto a sus cómplices.
Esas tres cartas o tres dedales, según la teoría de la probabilidad, son las ganadoras para los organizadores del juego, y luego está el juego de manos.
No hay juego de manos ni teoría de la improbabilidad. :) Todo es banal y sencillo. Lo sé de primera mano. Fue en la década de 1990 y el esquema me fue descrito con gran detalle por un hombre que estuvo involucrado en él. Ahora la gente no se deja engañar; los estafadores operan sobre todo en línea. Pero los principios básicos siguen siendo los mismos. Atraer a una persona, aprovecharse de sus debilidades y sacarle dinero, y luego, con cualquier pretexto, el dinero nunca se devuelve.
Las condiciones del juego no se describen completamente, como es habitual.
¿Es posible ganar más de lo apostado? Si no, no tiene sentido jugar.
Entonces se debería permitir ganar del bote. Así que basta con hacer la apuesta mínima, habrá una ganancia.
Tal vez la condición es que se puede jugar 1 vez, y aquí tenemos que decidir sobre la apuesta, por lo que habría la máxima probabilidad de ganar.
Como todos los "pradlocks" - de condiciones incompletas.
Solución:
Ni siquiera es cuestión de apostar. Apuesta 1. No tiene más sentido, la probabilidad de ganar no depende del tamaño de la apuesta. Así que 1, sólo para empezar el juego.
Entonces, ¿cuál es la paradoja? ¿Desde el punto de vista de que hay que hacer una apuesta mayor para aumentar las ganancias? Podría ser eso.
El punto del juego: para entrar en el juego se necesita un depósito y el juego de la moneda dura hasta que aparezca la primera águila (un juego de una sola vez), se gana 1-doucat cuando aparece un águila en la primera tirada, si había una cola y aparece un águila en la segunda tirada, la cantidad ganada se duplica, y así hasta el infinito, hasta que aparezca un águila. Probabilidad de ganar 1 ducado-0,5, 2-0,25, 4-0,125 etc., por lo que se puede ganar infinito, y jugar infinito, si el bote es infinito.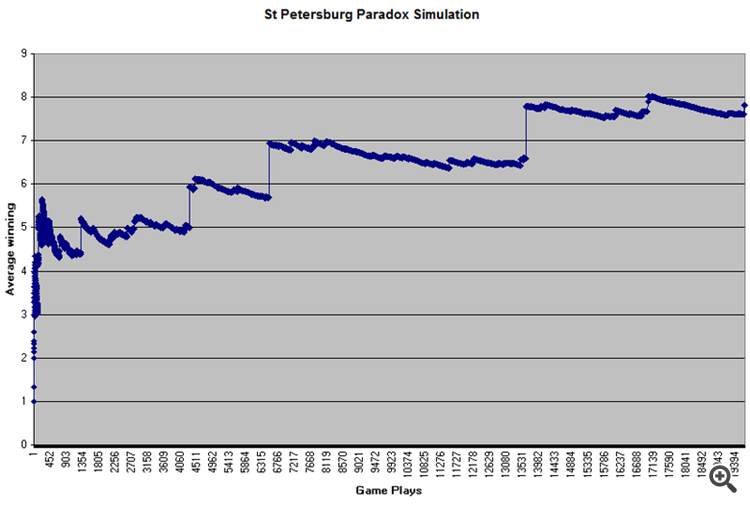
se trata de una función no lineal.
y=2^x.
y ¿a dónde tiende Y en una función no lineal si X tiende a infinito? correcto, a infinito.
Por lo tanto, si el número de juegos = infinito, entonces el promedio de ganancias = infinito.
Además, el problema está planteado de tal manera que sus pérdidas son una función lineal (siempre 25 rublos cada una), mientras que sus ganancias son una función no lineal.
Tienes que trazar dos funciones. Primero la primera gráfica será más alta que la segunda, luego se intercambiarán.
Todo depende del número de partidos.
Exactamente.
¿Pero qué pasa si necesitamos del 0 al 5, o al 7 o a cualquier otro número? Todavía tenemos que dividirlo por 32768,0. ¿O hay variantes?
1. Si no estás satisfecho con la calidad de la TRC (por ejemplo, con los bits bajos), entonces tienes que pasarla por AES.
2. Se puede tomar el resto de la división, pero sólo si se divide por potencias de 2. De lo contrario, por muy bueno que sea el GSF, el resultado no se parecerá en nada a una distribución uniforme.
3. Con la división por el doble se puede hacer un verdadero lío con sus comparaciones :-) En la mayoría de los casos se obtiene una salida pequeña, pero sesgada.
para obtener un número aleatorio de 0 a 6 (uno de 7):
- considerar límite=RAND_MAX - (RAND_MAX%7) ; el máximo múltiplo de 7 en el rango 0..RAND_MAX
- utilizar RDS hasta que obtengamos r<límite; es decir, si el "número aleatorio" es mayor que el límite, no podemos hacer nada con él: tomamos
- resultado = r % 7 o (para mejor o peor) r * 7 / límite
de alguna manera así :-) podría estar equivocado +-1,