Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
Sí
Por desgracia, no soy matemático.Todo lo que necesitas saber es el curso de álgebra de 8º grado. No hace falta ser matemático para hacerlo.
La distancia está marcada como d -- ver cómo se calcula.
¿Por qué es una mierda? ¿Por qué es una mierda?
Porque si se reproduce literalmente el código, se obtienen tonterías que serán diferentes en todos los gráficos.
No se pueden medir ángulos en un sistema de coordenadas que cambia constantemente. Su ángulo también cambiará.
En realidad, deberías decirnos por qué lo necesitas, tal vez todo el mundo ya esté usando otra solución para tu problema.
para entender de qué estamos hablando:
..................................................................
..................................................................
Sus imágenes muestran todos los puntos de intersección, pero en realidad el autor no tiene datos de coordenadas para los puntos de intersección con la segunda línea. No es obvio en las fotos cómo lo encontró.
En realidad, deberías decir por qué lo necesitas, tal vez todo el mundo ya esté utilizando una solución diferente para tu problema.
Necesito saber la diferencia entre dos líneas paralelas...
La línea roja es la distancia entre las líneas
hasta ahora esto es teoría - http://www.cleverstudents.ru/line_and_plane/distance_between_parallel_lines.html pero ¿cómo hacerlo en la práctica?En sus imágenes se conocen todos los puntos de intersección en todas partes, pero en realidad el autor no tiene las coordenadas de los puntos de contacto con la segunda línea. No es obvio en las fotos cómo lo encontró.
Las imágenes muestran todo el proceso de resolución del problema, incluida la determinación de los puntos de intersección.
Oleg avtomat2018.03.31 04:30#37
Las imágenes muestran todo el proceso de resolución del problema dado, incluida la definición de los puntos de intersección.
Oleg avtomat2018.03.31 04:30#37
Mirando atentamente la imagen (¿matlab aparentemente?)
Planteando una hipótesis, vemos dos funciones donde:
- "b" es el desplazamiento del eje y,
- "a" es el factor de inclinación,
- "t" es la coordenada del eje x.
- "z(t)" es la nueva función que describe la perpendicular
¿verdad?
Busco más y no puedo entender, las siguientes expresiones muestran qué - ¿dónde están las flechas y la inscripción "resolver"?
A continuación aparece "r" (¿lado del triángulo?) - ¿qué es y qué implica la fórmula con las palabras - grado?
A continuación se encuentra d, que es una especie de fórmula conocida...
Mirando atentamente la figura (¿matlab aparentemente?)
Puse una hipótesis, vemos dos funciones, donde:
- "b" es el desplazamiento del eje y,
- "a" es el factor de inclinación,
- "t" es la coordenada del eje x.
- "z(t)" es la nueva función que describe la perpendicular
¿verdad?
Busco más y no puedo entender, las siguientes expresiones muestran qué - ¿dónde están las flechas y la inscripción "resolver"?
A continuación aparece "r" (¿lado del triángulo?) - ¿qué es y qué implica la fórmula con las palabras - grado?
A continuación ya se encuentra d, más o menos por la fórmula que todo el mundo conoce...
matcad
a la derecha
"resolver" = "resolver" -- encontrar el punto de intersección de la recta con la perpendicular, es decir, encontrar el valor de t en el que y(t)=z(t)
sustituir el t encontrado y determinar r=y(t) en este t concreto
así, obtenemos las coordenadas de la intersección (t;r) para la primera línea
para la segunda línea realizar las mismas acciones
como resultado tenemos dos puntos, cuya distancia debe determinarse
determinar d mediante la fórmula
matcad
a la derecha
"resolver" = "resolver" -- encontrar el punto de intersección de la recta con la perpendicular, es decir, encontrar el valor de t en el que y(t)=z(t)
Tómate tu tiempo, significa resolver, ajá, pero no está claro cómo resolver. ¿Lo llevo a través de un sistema de ecuaciones?
Tómate tu tiempo, significa resolverlo, sí, pero no está claro cómo resolverlo. ¿Lo llevo a través de un sistema de ecuaciones?
Como quieras.
puedes hacerlo numéricamente, con un margen de error aceptable... no importa.
Pero en este caso es muy sencillo de resolver analíticamente.
permítanme recordarles que a dos rectas paralelas dadas se les puede trazar un número infinito de perpendiculares y cualquiera de ellas se puede utilizar para determinar la distancia
en particular es también una perpendicular a las líneas dadas :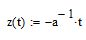
equiparando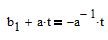
encontramos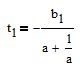
sustituyamos este valor en la ecuación de la línea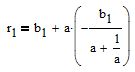
obtenemos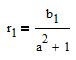
Se encuentra el primer punto (t1;r1). El segundo se determina de la misma manera.
Como puede verse, no hay nada complicado. Sólo hay que pensar un poco.